これまで14回に渡り「解法その1」~「解法その4」そして「色分けの手法」をご説明して来ましたが、第15回からその後数回に渡り最終回として、第1回の時にご紹介した「世界一難しい数独」の問題に「色分けの手法」を使って再度ご説明しています。
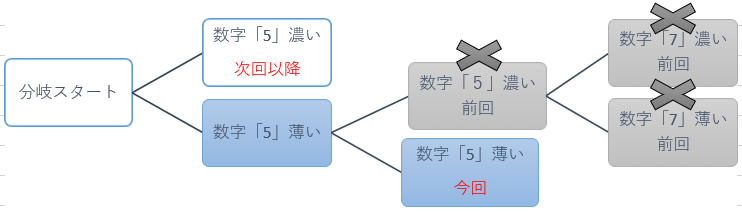
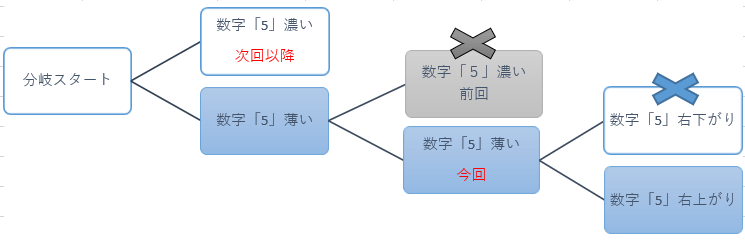
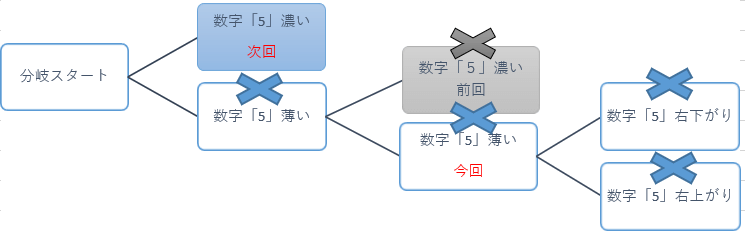
前回は左図で×印のところをご説明しましたが、今回は最初の数字「5」「薄い」の二択分岐の残りの二回目の数字「5」「薄い」の場合になります。
今回の説明で使用する数独問題について
第1回の時にもご紹介していますが、今回の問題は2012/7/3日付の「ロケットニュース24」に掲載されている「世界一難しい数独」になります。
二回目の二択分岐その2「薄い」「5」で仮置きをした盤面
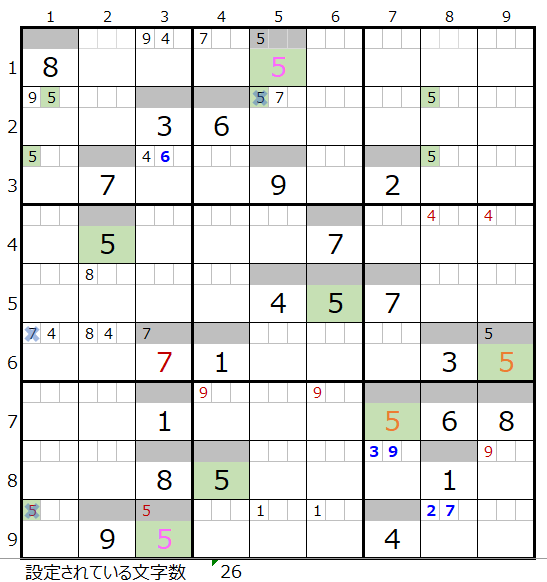
この盤面は第16回「世界一難しい数独その2」からの続きになります。
文字数は26文字まで来ていますが本解法その1から3では盤面として行き詰まった状態です。
左図のメモ欄
・黒字茶字—解法その1からセット
・太青—解法その3からセット
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれている物を除き)1から9の各数字でメモ欄にその数字が置ける場所の数は次の通りになります。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 19 | 39 | 28 | 17 | 0 | 27 | 14 | 19 | 20 |
数字「7」が14か所となり、この状況の中では一番少ないので「7」を考えて見ます。
ただし左図のような色分けの正しい連鎖が見つかるのですが、よく見ると対角で置き換え可能なポイントが4ヶ所もあるので数字「7」を候補にするのは難しい認識です。
残念ながらその他相対的に少ない数字「4」「1」「8」「9」も確認したのですが、複数連鎖の対処法では『「濃い」「薄い」でそれぞれ2つ以上共通して通過するマス目が存在する』数字は存在していませんでした。
という事で、今回選択すると三回目となる数字「5」で再度考える事にします。
ただし、数字「5」は残り2ブロックで配置はスクウェアですので「色分けの手法」ではなく「二択分岐する」ということになります。
三回目の二択分岐となる数字「5」
スクウェアの配置ですので選択するのは対角の2か所になります。
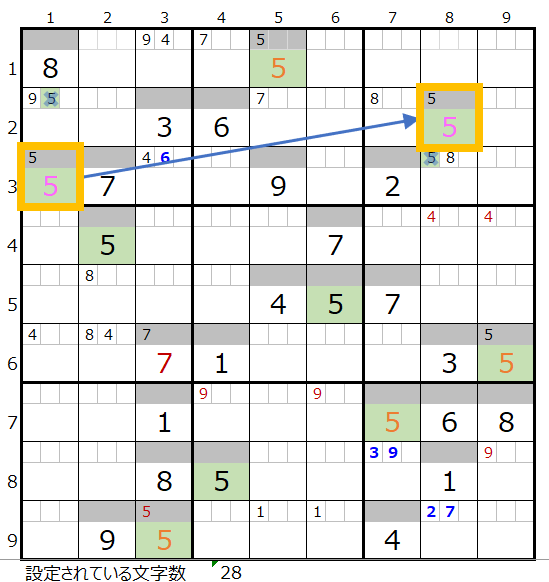
この「右上がり」と「右下がり」の2パターンで二択分岐して解き進めることにします。
二択分岐「右下がり」での盤面
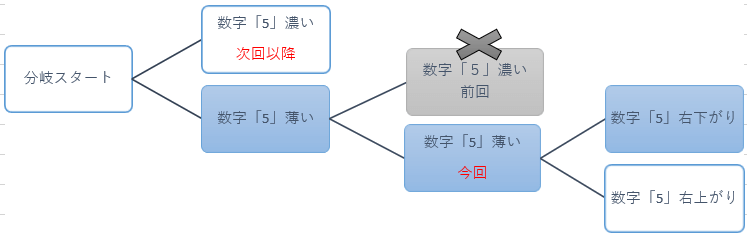
この章でご説明するのは左図の数字「5」右下がりの場合です。
数字「5」右上がりにつきましては後段でご説明致します。
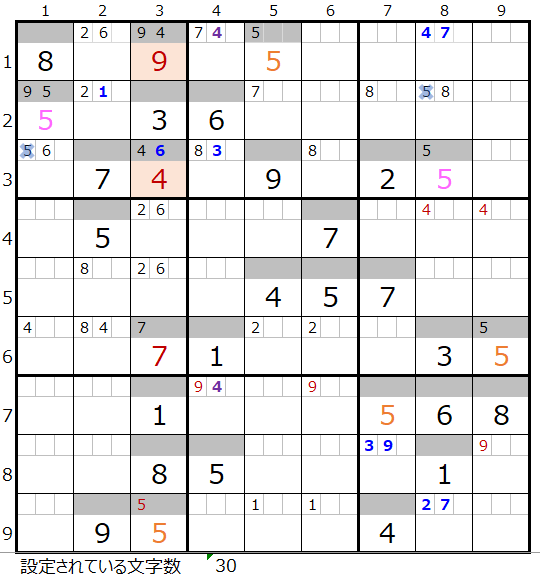
「右下がり」にセットされた数字「5」により、解法その1からその3で解き進めると、左図背景色を付けた2か所の数字が確定します。
なおメモ欄については背景色は省略しています。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 18 | 28 | 27 | 12 | 0 | 17 | 13 | 12 | 17 |
数字「4」と「8」が同数で12ヶ所となります。
両者を盤面で見比べて見ます。背景色薄ピンク色のところが該当の数字が置ける場所です。
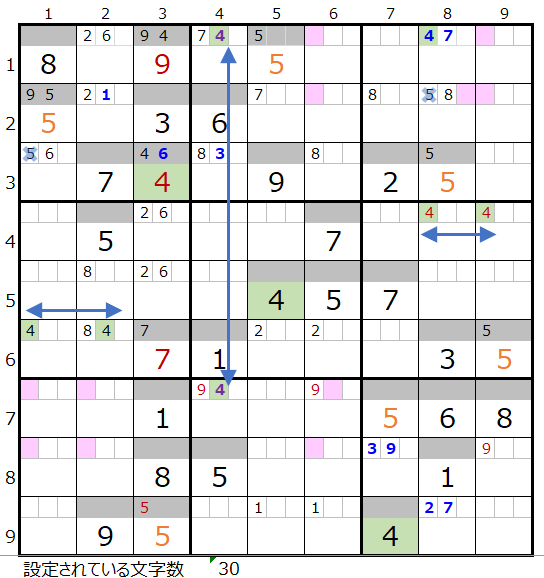
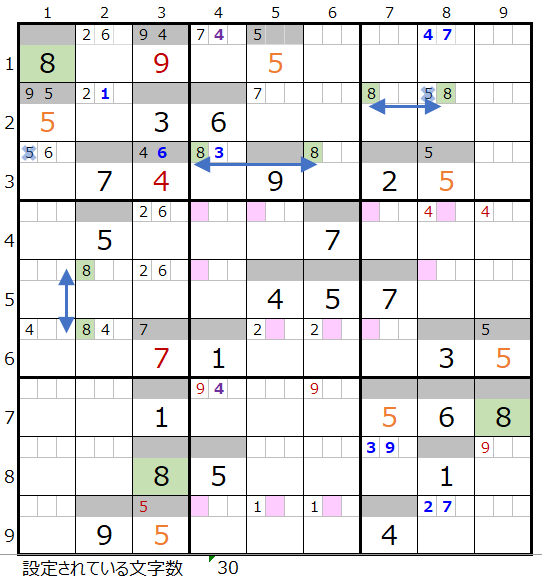
メモ欄の状況に関しても両者差が無さそうです。
となると連鎖を調べて対角で置き換え可能なポイントの数を見比べることにします。
それぞれ上図のような色分けの正しい連鎖があることが解ります。
対角で置き換えが可能なポイントは数字「4」が3ヶ所であるのに対して、数字「8」は2か所ですのでポイントの少ない「2」を選択することにします。
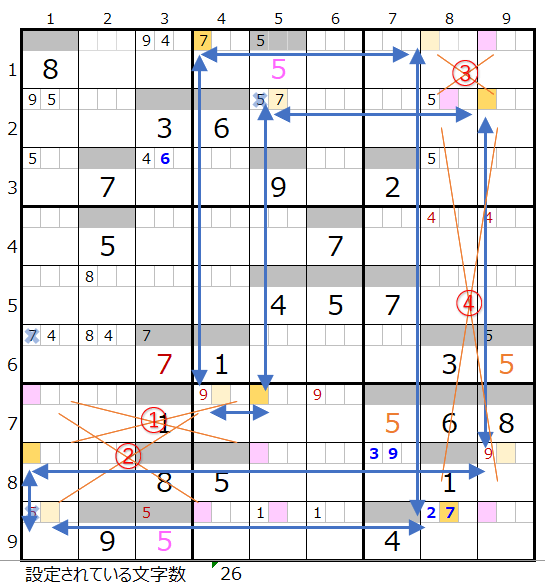
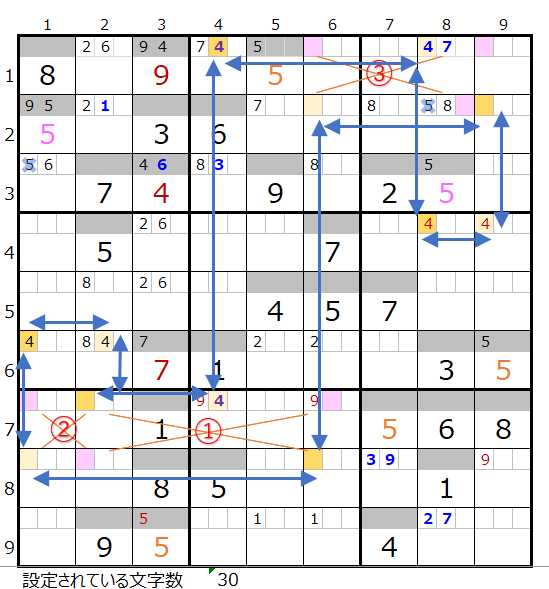
数字「8」の連鎖を調べる
上右図にある①と②の置き換えを確認して行きます。
①を置き換えだ場合は2つのループとなるために対象外となります。
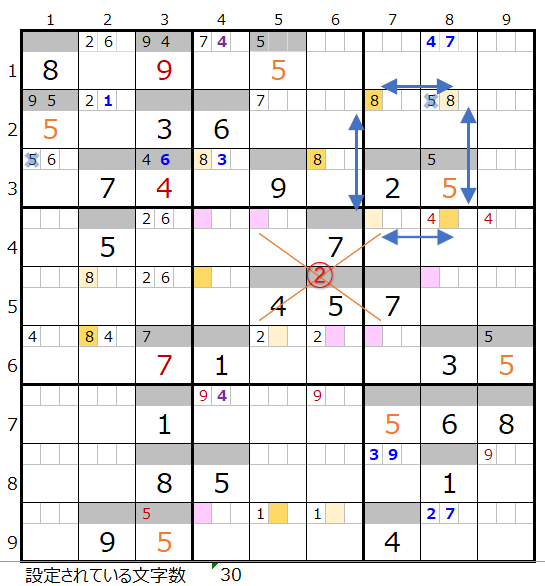
②を置き換えた場合はスクウェアとそれ以外のループとなるため対象外となります。
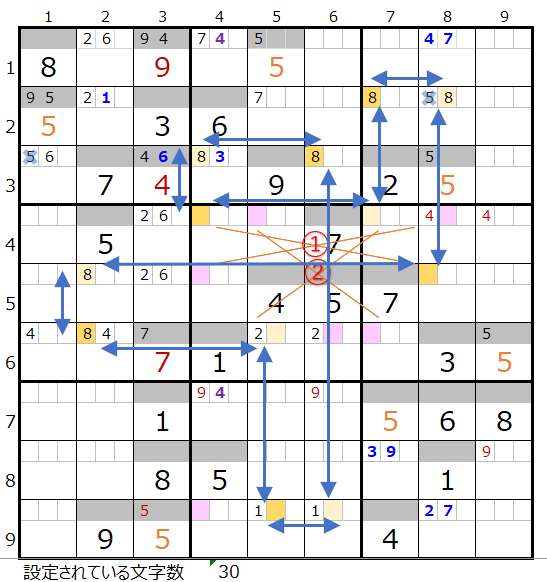
最後に①と②をともに置き換えだ場合は色分けの正しい連鎖となります。
なおこの3つのパターンの中には「新たに見つかった置き換え可能なポイント」はありませんでした。
そうなると成立した2つの連鎖以外に連鎖は無く、この2つで「共通して通過するマス目」を確認することになります。
共通して通過するマス目は左図のように「濃い」「薄い」それぞれ4ヶ所づつ存在します。
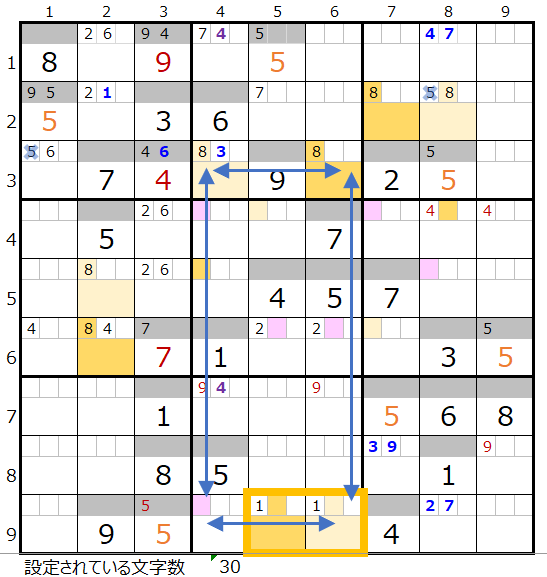
ただし左図紺矢印のところに「スクウェアになる可能性がある部分」が含まれています。
経験則として「共通して通過するマス目の中にスクウェアになり得る箇所が存在する」場合は当該数字はあきらめる必要があるのですが、このまま諦めてしまうのは残念です。
そこで「おきて破り」になりますが、数字「8」は採用しつつ、スクウェアの対角となる可能性のある黄枠の部分は除外して適用することにします。
四回目の二択分岐となる数字「8」
「濃い」「薄い」に数字「8」をセットした盤面はそれぞれ下記のようになります。
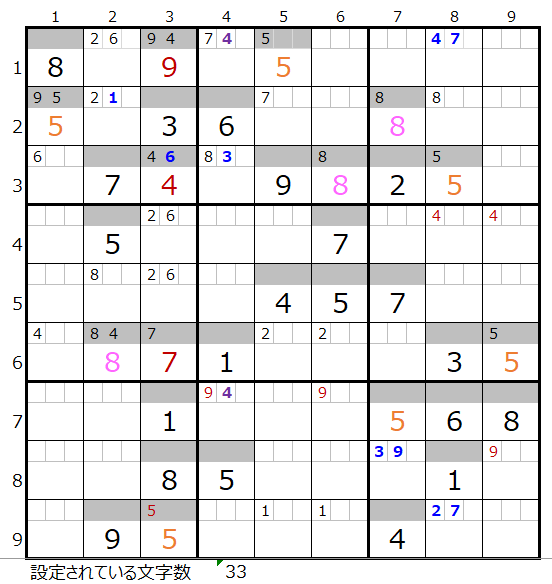
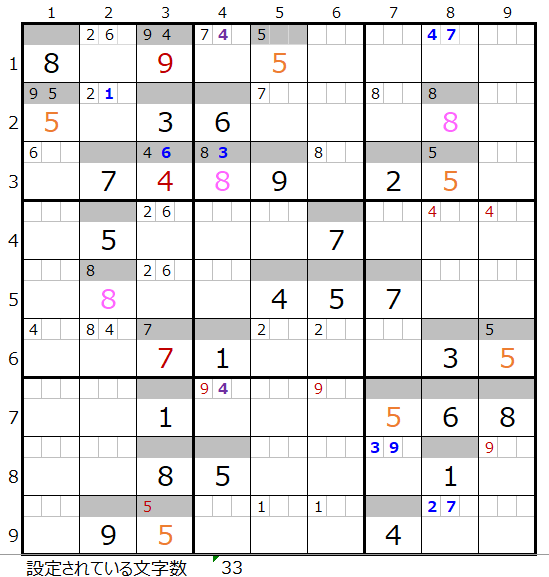
両者を解き進めるとそれぞれ下記盤面になります。
残念ながら両者ともに途中で手詰まり(解けない)という結果になります。
第8ブロックに「6」が入らない。
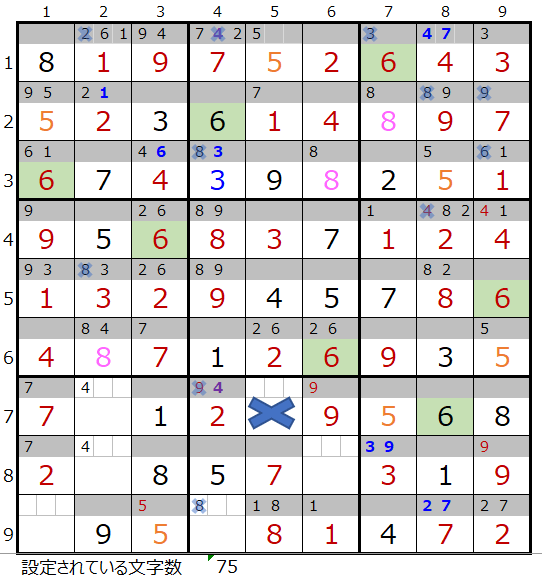
7・8行目と4列目には数字「1」と「6」が存在しているため、黄枠のメモ欄は成立しています。
7・8行目には数字「8」があり「薄い」で4列目に「8」が入ると、第8ブロックに「8」が入らないことになります。
以上により二択分岐「右下がり」のルートには正解が存在しない事が解りました。
続けて二択分岐「右上がり」についてご説明致します。
二択分岐「右上がり」での盤面
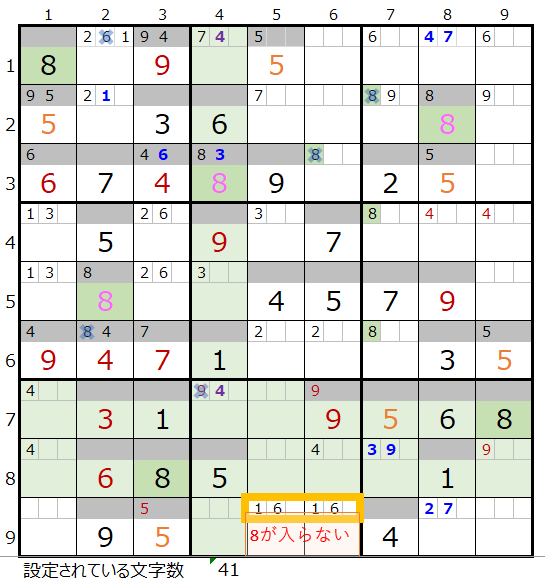
『三回目の数字「5」右下がり』には正解が無い事が解りましたので、もう片方の『数字「5」右上がり』を見て行きます。
メモ欄で該当する数字が置ける場所を確認する
「右下がり」の場合と同様に、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 18 | 39 | 28 | 15 | 0 | 26 | 11 | 16 | 19 |
数字「7」が11か所になるので「7」を選択します。
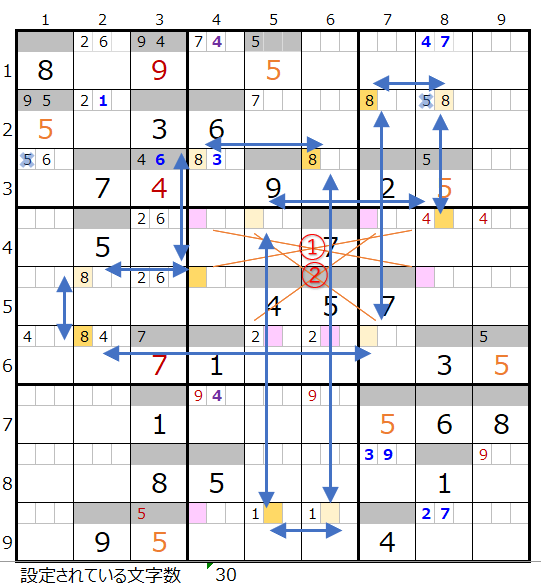
数字「7」で連鎖を考える
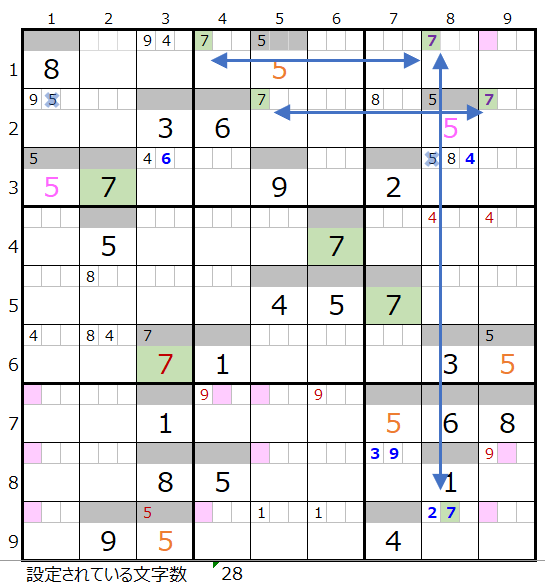
メモ欄にセットされた数字で紐づけできるところを結ぶと上左図のようになります。
「第7ブロックをどのように通過させるか?」を考えると連鎖を見つけ易いと思います。
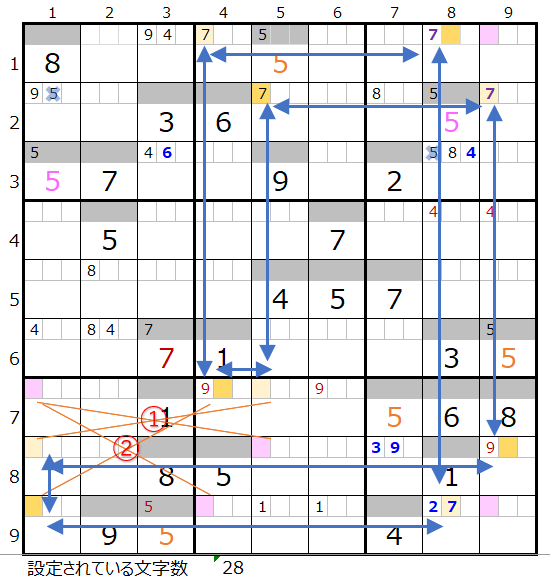
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換え可能なポイントは2ヶ所(①と②)になります。
①を置き換えて見るとスクウェアができるので対象外となります。
なお上左図のようにもう一つの連鎖(■の×印)が成立することが解ります。
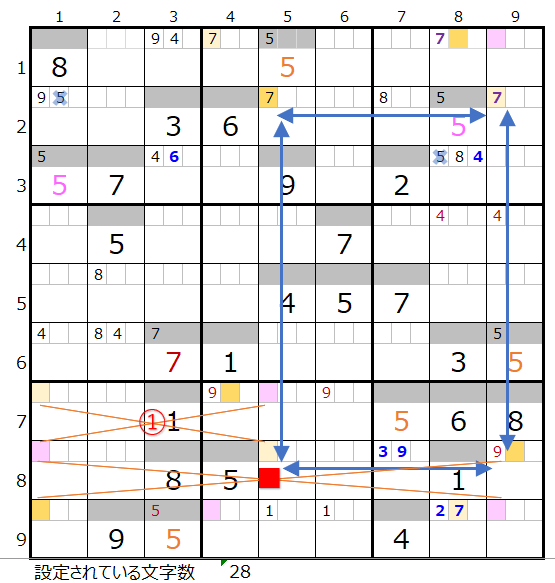
■×印を置き換えると上右図のように色分けの正しいもう一つの連鎖があることが解ります。
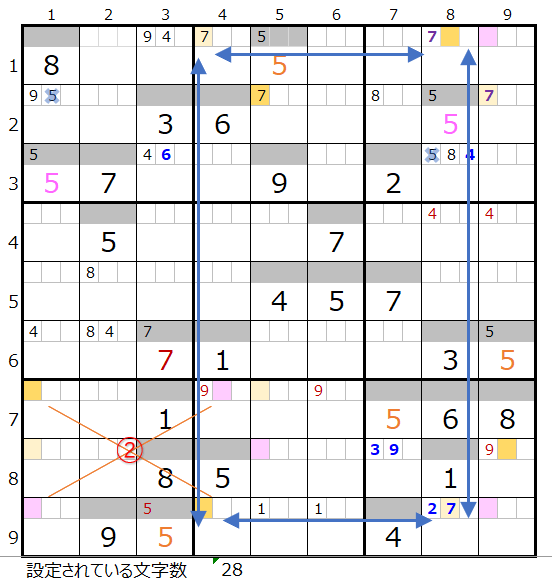
最後に②を置き換えると、上左図のようにスクウェアができるので対象外となります。
なお①と②同時の置き換えは数字の配置として成立しません。
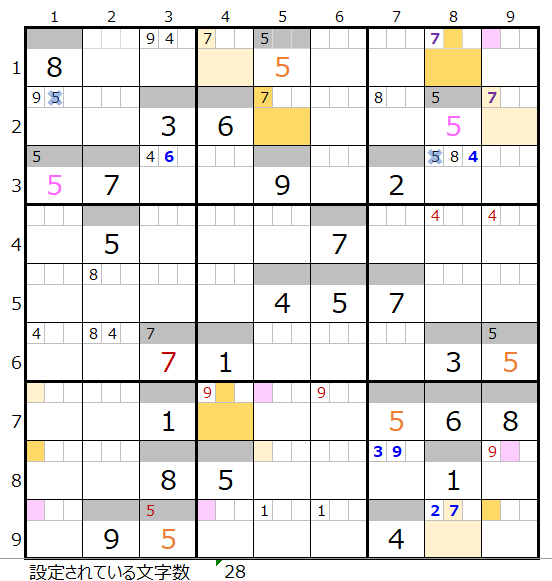
2つの連鎖で共通して通過するマス目に「濃い」「薄い」で背景色を付けると上右図のようになります。
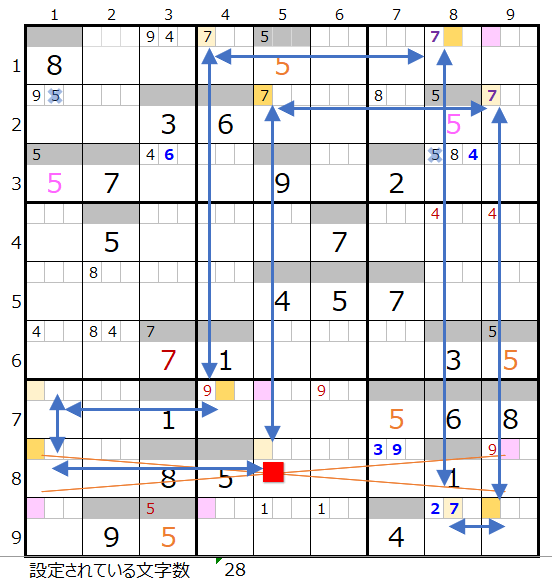
この情報をもとに「濃い」「薄い」での二択分岐をして行きます。
四回目の二択分岐「7」で「濃い」「薄い」
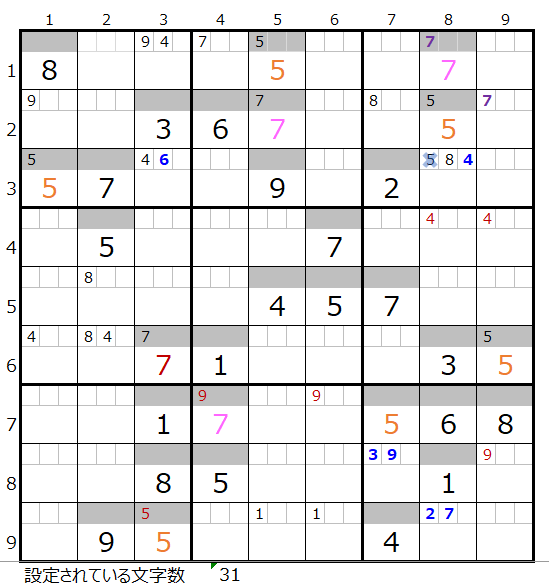
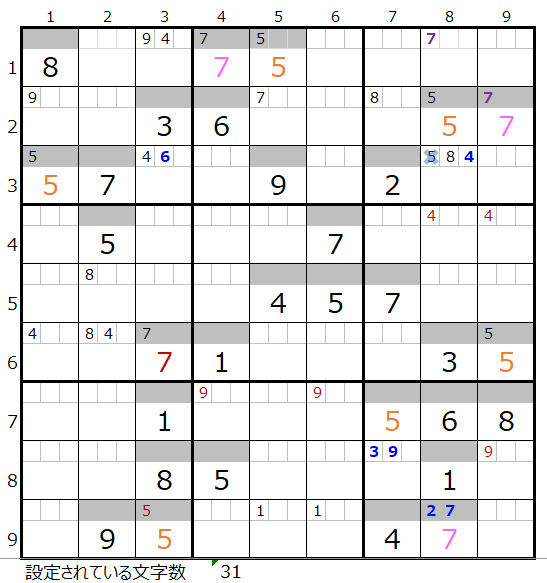
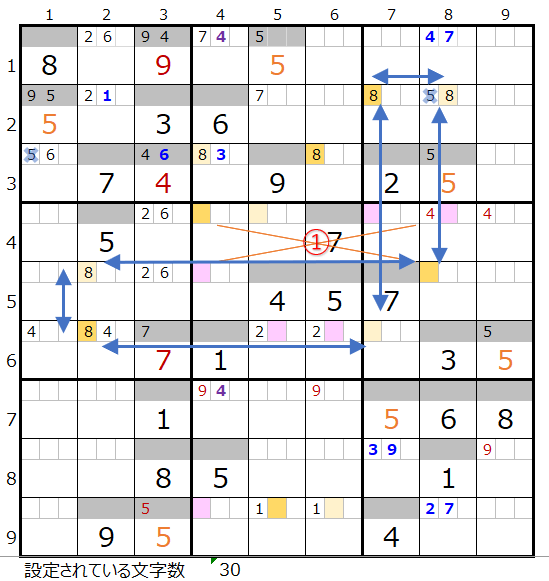
両者を解き進めるとそれぞれ下記盤面になります。
残念ながら「濃い」は途中で手詰まり(解けない)という結果になります。
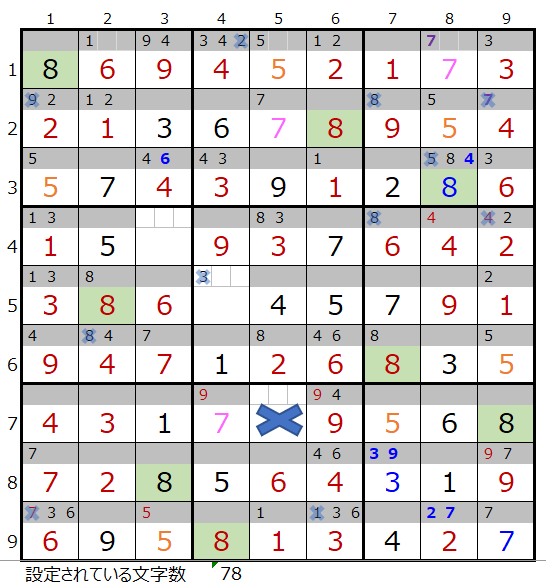
第8ブロックに数字「8」が入らない事が解ります。
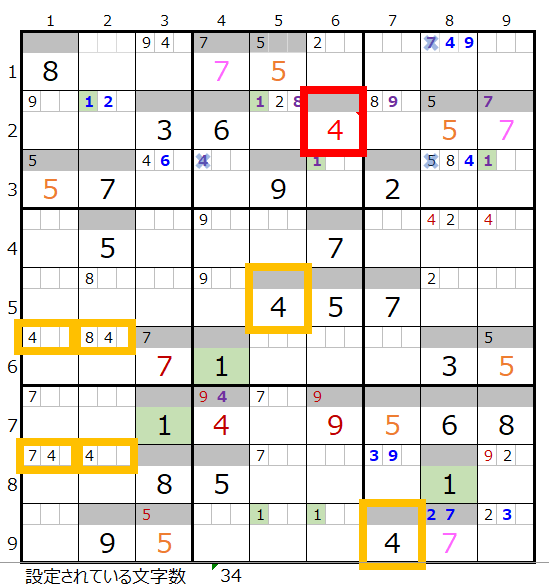
解法その1から3では上右図まで解き進める事ができます。
赤枠の数字「4」は黄枠の「4」の配置から決まります。
この後さらに「薄い」を解き進めて行きます。
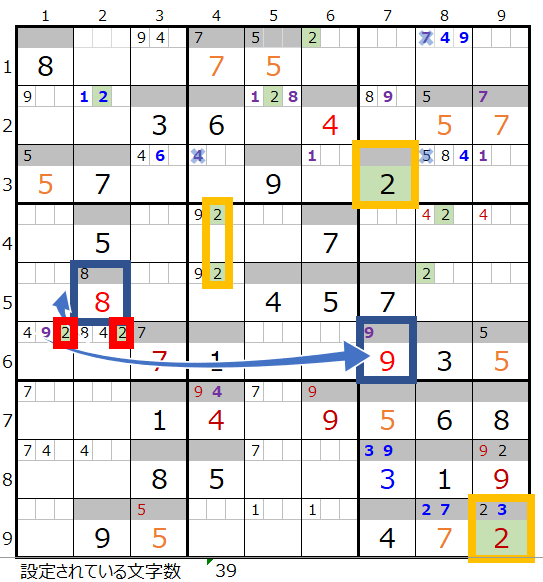
次に数字「2」は黄枠の配置から、第4ブロックメモ欄の赤枠の「2」が決まります。
それにより紺枠の数字「8」と「9」が決まります。
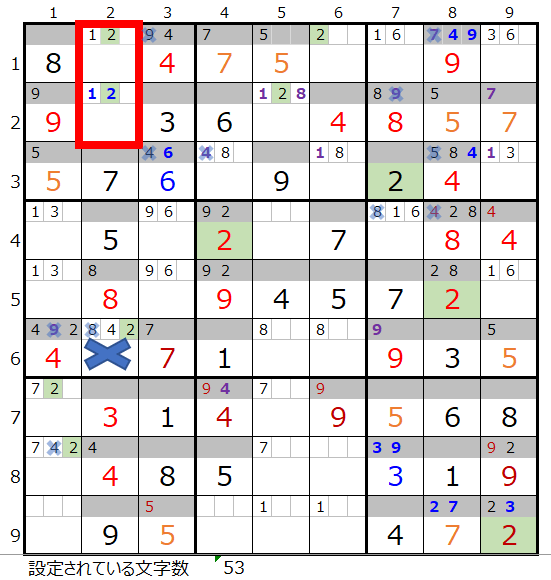
さらに「薄い」を解き進めると赤枠メモ欄の数字「2」の情報と第4ブロック×印のに入る「2」が矛盾することになり、これ以上解けない事が解ります。
まとめ
今回は数字「5」での二回目の二択分岐で「薄い」場合のルートの最後までをご説明致しましたが、これにより一回目の二択分岐の「薄い」場合の確認がすべて完了したことになります。
数字「8」まで
数字「7」
数字「7」数字「1」まで
次回は『数字「5」の一回目の二択分岐「濃い」 』 のその先についてご説明したく存じます。
最後までご一読いただき誠にありがとうございました。


