前回第10回では「色分け手法」の手順についてご説明しましたが、「色分け手法」の中の「色分の正誤を判断するための手法」についてはご説明できませんでした。
今回は連鎖の見つけ方と合わせて「色分の正誤を判断するための手法」についてご説明したく存じます。
今回の説明で使用する数独問題について
今回もいままでと同じく下記サイトの2015年11月の問題集を使用させていただいています。
今回の問題は「数独問題集(達人級)」の2015/11/08下段に掲載されています。
これまでと同様に途中から使用させていただいておりますが、コピーライトは問題を作られている数独無料問題集様がお持ちのものになりますので初期の盤面につきましては、上記サイトにてご確認いただけますようお願い申し上げます。
「解法その3」終了時の盤面
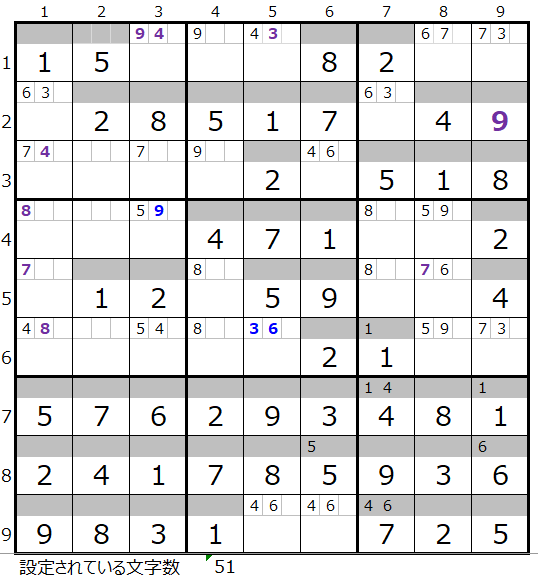
左図のメモ欄
・黒字—解法その1からセット
・太紫—解法その2からセット
・太青—解法その3からセット
解法その1から3により文字数は51文字まで解かれていますが、盤面としては行き詰まった状態です。
※2行9列のマス目の太紫の「9」は解法その2で求められています。
メモ欄にセットされている数字の状況を1~9すべて確認する
前回第9回でご説明した「色分け手法」の手順に従い、ブロックに入る可能性のある箇所のメモ欄の背景色を薄ピンクにセットして行きます。
※数字の「1」と「2」は9ブロックすべてにセットが完了しているので画面ショットは省略致します。
なお説明のために可能性のある箇所の個数を数えていますが、ざっくりと難易度だけ把握すれば大丈夫です。
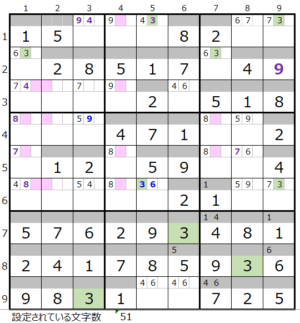 数字「3」–13ヶ所
数字「3」–13ヶ所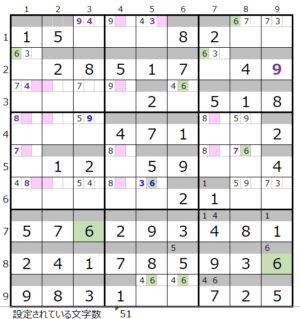 数字「6」–14ヶ所
数字「6」–14ヶ所 数字「9」–5ヶ所
数字「9」–5ヶ所
 数字「4」–1ヶ所
数字「4」–1ヶ所 数字「7」–2ヶ所
数字「7」–2ヶ所
 数字「5」–0ヶ所
数字「5」–0ヶ所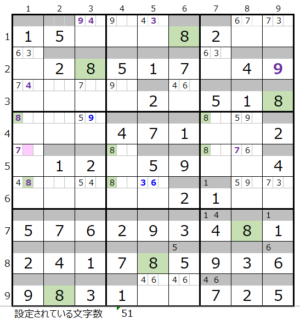 数字「8」–1ヶ所
数字「8」–1ヶ所
難易度の低い数字の連鎖を考える
今回の問題では前回第9回の問題のような特異点は存在していません。
※経験上で恐縮ですが、特異点がある方が少ない認識です。ただ存在している場合には見逃さないようにすべきです。
対象となる数字の候補としては「4—1ヶ所」、「7—2ヶ所」、「8—1ヶ所」、「9—5ヶ所」となりますが、今回は「4」から順番に調べて見たいと思います。
※なお実際には一つの数字で連鎖が一つであることが解り、その数字で「色分の正誤を判断するための手法」を用いてどっちのパターンであるか?判定し、それによって対象の数字が決まればすべてを調べる必要はありません。
ところで可能性のあるマス目を含めてすべての連鎖パターンを見出すのはなかなかむがすしぃ作業ですが、前回も書きましたが大切なルールがありますので今回と同様になりますが再度掲載致します。
ルールとしては「下記の場所は必ず通るように連鎖を考える」ことになります。
連鎖は残りのすべてのブロックを通過するルートでまずは考える
最初は残りのすべてのブロックを通るルートを捜します。
経験上、調べると何かしらのルートは存在していものです。
ただし前回第9回の問題もそうでしたが数字の置かれ方によっては残りのすべてのブロックを通過するルートが存在しない場合がございます。
このような場合は残りの中からいづれか1ブロックを減らして、減らした形でルートが存在しないかを確認します。
この理由は連鎖を分割した時に分かれたブロックの数が3ブロック以下になってしまうと「色分の正誤を判断するための手法」をしても有効な結果を得られないためです。
減らす際の注意点としては「減らした状態ですべてのブロックを通過するルートはユニークである」必要があります。
実はこの制約は厳しくて、残りすべてを追加するルートはユニークであっても減らした状態ですべてのブロックを通過するルートが複数存在する事が往々にしてあります。
そんなると残念ながら該当数字を対象にするのは諦めるしかありません。
①数字「4」で連鎖を考える
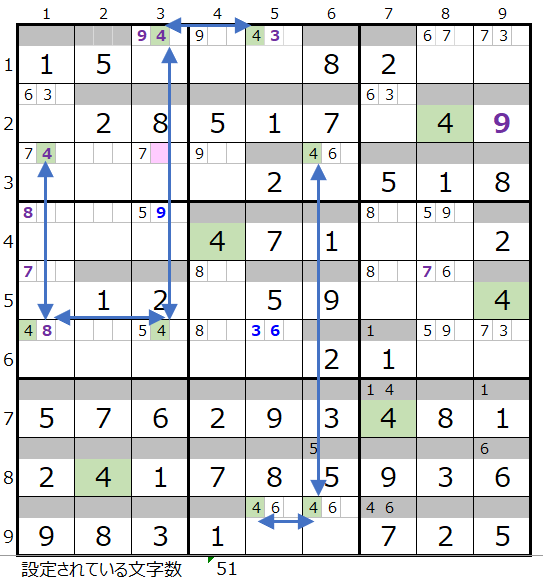
左図の紺矢印は上記の2番ルールにより結ばれています。
まは紺四角は必ず通過する必要がある場所になります。
このような情報があるので連鎖のルートを見つけるのは難しくないと思います。
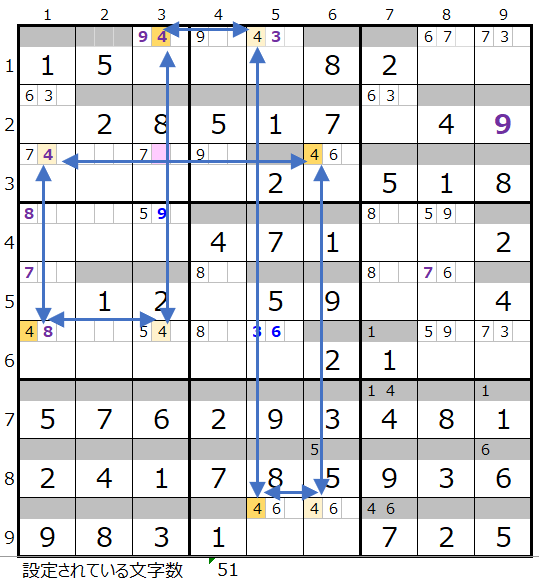
「濃い」「薄い」の色分けも左図のように規則正しいので、4つのブロックをすべて通過する連鎖のルートはこれだけになる認識です。
なお「連鎖のルートが他に存在しないか?」を正しく確認するという事は難しい事と認識しています。
ただし、連鎖がユニークでないと「色分の正誤を判断するための手法」を実施しても経験上有効な結果を得られないことになりますので、ここは是非とも押さえておきたいポイントになります。
ちなみに上図において、もしも薄ピンク色のついたマス目を選択した場合、横方向の場合は第2ブロックの1行5列、縦方向の場合は第4ブロックの6行1列で解法その1から数字が決まることになり、4つのブロックをすべて通過する連鎖のルートにはならない事になります。
このようなケースは割と良くありますので覚えて置くと良いかもしれません。
連鎖を考える対象から除いた方が良いケース
連鎖を考える対象から除いた方が良いのは下記の場合です。
- 該当数字がセットされていないマス目のメモ欄がすべて確定した状態でセットされている。
- 確定とは背景色薄ピンク色のマス目が存在しないとともに、縦方向、横方向で該当数字が入っているのは2ヶ所だけの状態を表します。
- この場合はセットされている該当数字をすべて結べば連鎖ができるはずです。
- 残りのブロックが3以下
- この場合は得られる効果が少ないので、他に選択する数字が存在しなかった時まで取っておく、言い方を変えると後ましにするのが良いです。
「色分の正誤を判断するための手法」が成立するための連鎖の条件
連鎖が見つかった後「色分の正誤を判断するための手法」に進むためには上記のケース以外で次の条件が必要になります。
- 連鎖の数字を「濃い」「薄い」で色分けした時に設定したブロックすべてが「濃い」「薄い」のペアになっている必要があります。
- もしも、1ブロックでも「濃い」「濃い」もしくは「薄い」「薄い」のペアが存在する場合は、その連鎖は採用することができません。
この理由は「濃い」または「薄い」のいずれかを選択し対象の数字をセットすることになるのですが、同じペアがあるという事は、1つのブロックに同じ数字が存在することになり、数独的にはあり得ないことになります。
- もしも、1ブロックでも「濃い」「濃い」もしくは「薄い」「薄い」のペアが存在する場合は、その連鎖は採用することができません。
- 横方向、縦方向の並びで同じ数字は必ず2つでなければなりません。
- 1つとか3つ以上になっているとしたら、その連鎖は採用することができません。
- 連鎖はユニークである必要があります。
- 同じ数字で連鎖が複数ある場合には残念ながら対応できる場合とできない場合があります。従いまして「どうしても複数連鎖しか存在しない」という場合を除いて除外することにします。
- 複数ルートがある場合、多くはその中のどれかに半分以上の正解がが存在するはずですが、それを何かしらの手法で判断する事ができれば良いのですがそりような手法は持ち合わせていません。
- 複数ルートの中に共通して通過するマス目は存在しますが、それが正解のマス目だけの場合とそうでない場合とに分かれます。
- 正解でないマス目になっている時は「色分の正誤を判断するための手法」を使っても間違っている部分を取り除くことができません。そのためあきらめざるを得ないことになります。
- なお複数連鎖の場合の対処法につきましては別の回で取り上げる予定です。
- 同じ数字で連鎖が複数ある場合には残念ながら対応できる場合とできない場合があります。従いまして「どうしても複数連鎖しか存在しない」という場合を除いて除外することにします。
②数字「7」で連鎖を考える
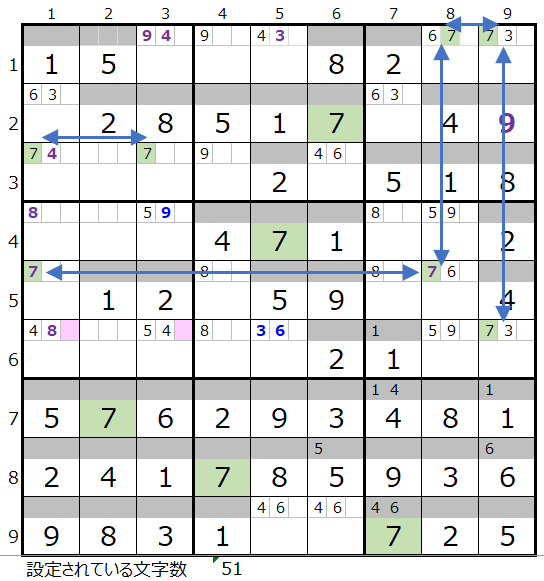
背景色薄ピンク色が2か所ですが如何でしょうか?
2ヶ所の内の6行3列を使えばよさそうです。
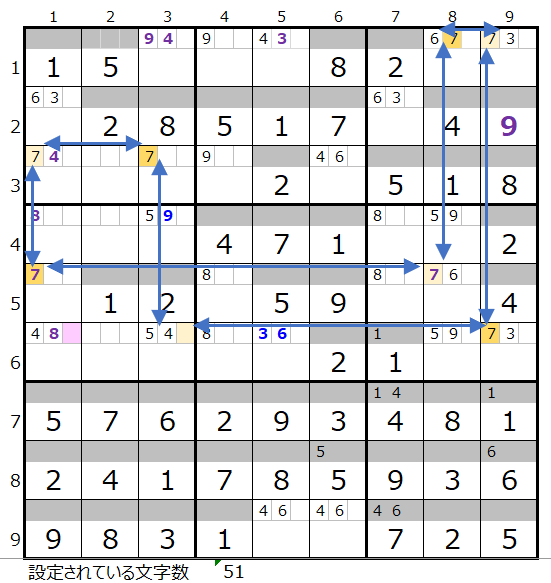
数字「4」と同じく「濃い」「薄い」の色分けも左図のように規則正しいので、4つのブロックをすべて通過する連鎖のルートはこれだけになる認識です。
なおこれしか連鎖のルートが存在しない理由も数字「4」の場合と同様になります。
③数字「8」で連鎖を考える
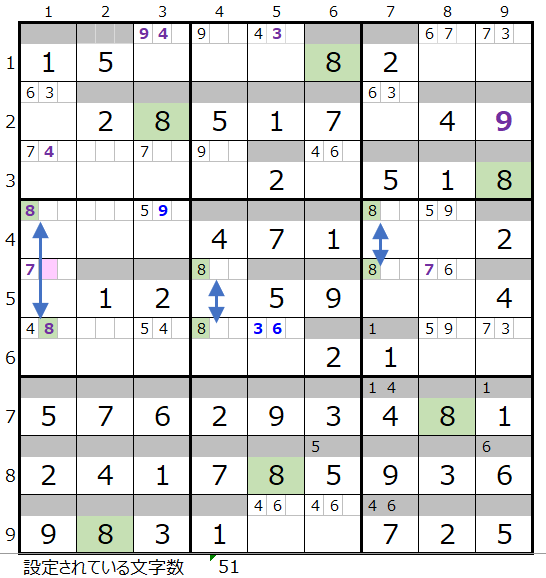
タイトル「連鎖を考える対象から除いた方が良いケース」で記載した「残りのブロックが3以下」に該当し、後回しにした方が良いのですが、ご説明のために取り上げています。
背景色薄ピンク色のマス目は解法その2の紺矢印で通過するので残りのマス目とつなげることで連鎖を作ることができます。
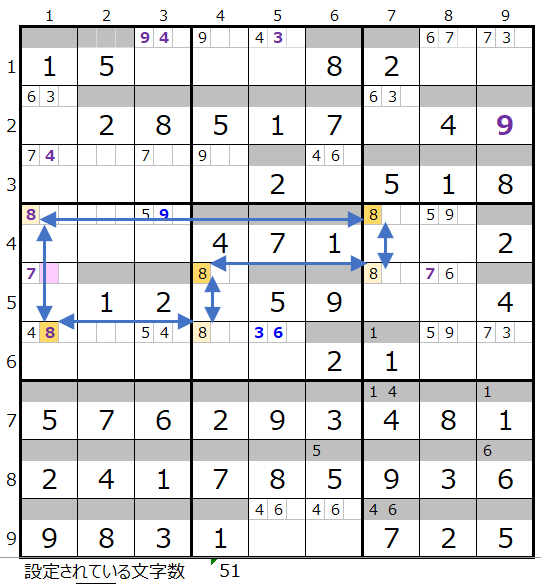
3ブロックをつなげる連鎖はこのルートしか存在しない認識です。
④数字「9」で連鎖を考える
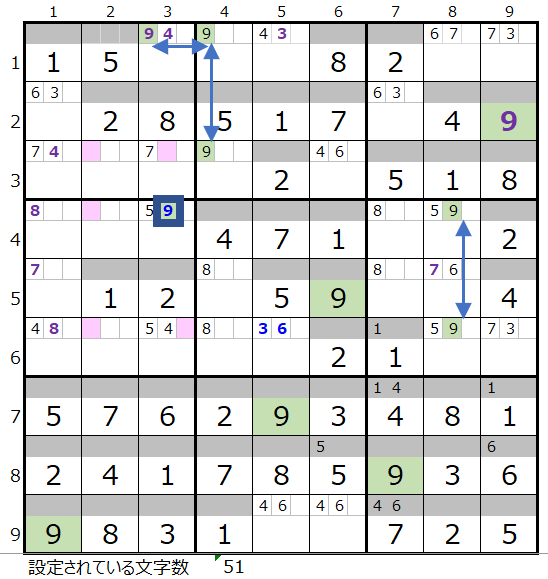
数字「9」ですが、背景色薄ピンク色が5ヶ所と多い割には、得られている情報が少ないので、ちょっと難しくなっています。
ただしブロック内で残り2か所となっている場合、その配置が横方向、縦方向で同じ行、同じ列に並んでいる場合はつぎのような制限があります。
横方向であれば、上か下(上の上、下の下もありえます)のブロックから入ってくるルートしかありません。
同様に縦方向であれば右か左(右の右、左の左もありえます)となります。
左図では第2ブロックと第6ブロックが該当します。
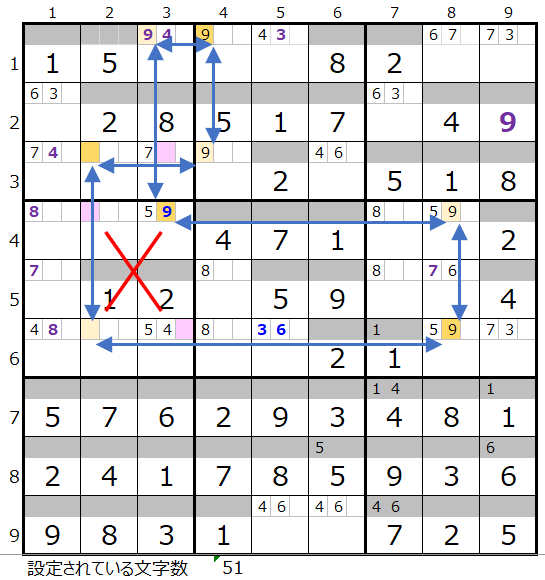
そうすると連鎖のルートとしては左図の形が見つかります。
ただし、左図赤線×印のところを見ていただきたいのですが、対角ではルートに含まれているのに対して、反対側の対角が背景色薄ピンク色で残っています。
このような場合、反対側の対角を通過するルートの存在が疑われます。
このようなケースだけではなく、やはり反対側の対角の数が多い場合は、必ず別のルートが無いか?確認する必要があります。
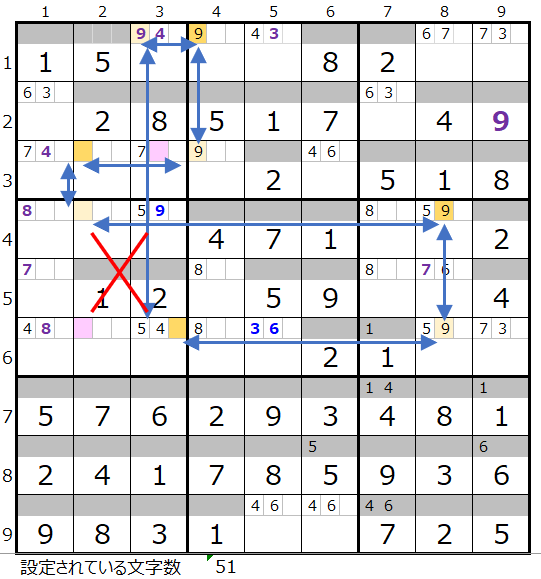
案の定、左図の形の別ルートが存在することが解ります。
このように複数のルートが存在する時はタイトル『「色分の正誤を判断するための手法」が成立するための連鎖の条件』で記載しましたが、連鎖がユニークでないと本手法を適用する事ができません。
この段階でルートがユニークに絞り込めれば、この後の展開で更なる絞り込みが考えられるのですが、複数ルートが存在する場合は別のやり方でいくつかのマス目を特定できる場合とできない場合があります。解けない場合もありますので対象からは除外することにします。
その他のブロックを減少させた連鎖のルートとしては下記のような形があります。
3ブロックーーその1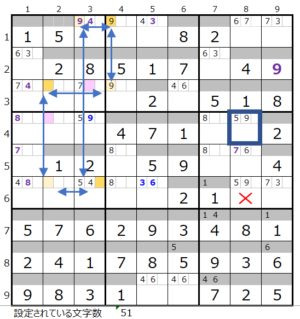 2ブロックでの連鎖が2つ
2ブロックでの連鎖が2つ
3ブロックーーその2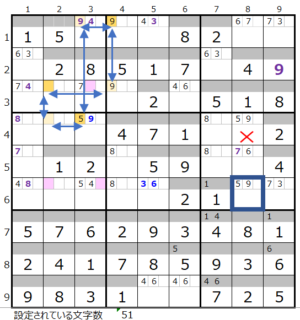 2ブロックでの連鎖が1つーーーその1
2ブロックでの連鎖が1つーーーその1
3ブロックーーその3 2ブロックでの連鎖が1つーーーその2
2ブロックでの連鎖が1つーーーその2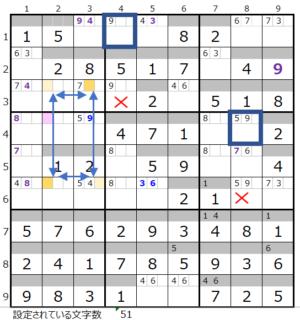
全部で8パターンの連鎖の中には正解を捕らえたものがあるものと推察致しますが、残念ながらそれがとれになるか?を絞り込む手法を見つけられていません。
今連鎖のバリエーションをご紹介したくすべてのパターンについて調べましたが、本来は複数ルートがある事さえ判明すれば十分で、該当数字は諦めて別な数字を探すことになります。
「色分の正誤を判断するための手法」を使った解き方
ここまでで、難易度の低い数字の連鎖は全て調べ終わりましたので、次のステップである「色分の正誤を判断するための手法」の具体的な説明に入ります。
タイトル『「色分の正誤を判断するための手法」が成立するための連鎖の条件』でも記載しましたが、条件としては連鎖がユニークである必要があります。
となりますと調べた数字の中で対象となるのは「4」「7」「8」です。そのうちの「8」は3ブロックのため本来は後回しにするのですが、今回は手法を説明する上では手っ取り早くできるので、まずは数字の「8」から調べることにします。
「色分の正誤を判断するための手法」で解る事
見つけ出された連鎖なのですが、『色分けされた「濃い」「薄い」のどちらかのパターンが正解になるのか?』といいますと、残念ながら結果的に「そうなる場合」と、「そうでは無い場合」の2つに分かれます。
結果的に「そうなる場合」というは、実際に問題を解いて見て振り返った時に「あの連鎖は正解だったんだ」と解る事を意味しており、端的には「問題を解く前には判らない」ということになります。
言い回しが回りくどくて恐縮ですが手法としては「そうならない場合」つまり安全性が高い場合を選択して解き進める事を想定しています。ただし稀に「そうなる場合」もありますので万が一そうなってしまった場合でも間違いではありませんのでご安心ください。
それでは「そうでは無い場合」というのは「見つかった連鎖の内のどの程度の部分が判明するのか?」という事が気になる事と存じますが、その答えは「半分以上」となります。
半分以上を具体的にご説明すると、残り4ブロックであれば2ブロック、残り5ブロックであれば3ブロック、以下同様に残り6ブロックであれば3ブロック、残り7ブロックであれば4ブロックが判明することを想定しています。
「色分の正誤を判断するための手法」とは
「色分の正誤を判断するための手法」は、次のような手順で作業を進めます。
- 連鎖の通過する各マス目に実際に1ヶ所づつ数字をセットして、その数字がどこまで解けるか?を調べて行きます。
- いままでの経験上どこまで解けるか?の下記の4つのパターンになります。
- すべてが解ける
- 半分以上が解ける
- 半分未満が解ける
- 仮置きしたマス目以外は解けない
- いままでの経験上どこまで解けるか?の下記の4つのパターンになります。
- 解けた場所が半分以上の箇所が「濃い」「薄い」で何か所づつあるか?を数えます。
- この時、すべて解けた場合は「1」とし、半分以上解けた場合は「解けたブロック数÷残りのブロック数」でカウントし、半分に満たない箇所はカウントから除外します。
- すべての箇所を調べ終わった時点で、「濃い」「薄い」のカウントをそれぞれ足し上げて見ます。
- いままでの経験上足し上げた結果は下記の何れかのパターンになります。
- どちらかが明確に大きい
- 明確な差がでない
- まったく同じになる
- 明確な差ではない代表的なパターンとしては下記のようなものがあります。
- 「1,1,1,1」と「1,1,3/5,3/5,3/5」—左の合計は1/5大きいが、箇所は右が多い
- いままでの経験上足し上げた結果は下記の何れかのパターンになります。
- 明確な差が生じていたら大きい方の「濃い」「薄い」から「1」ではない半分以上解けた時の配置を選び二択分岐をします。
- 万が一「1」のみになった時は、すべての連鎖が対象になります。
- 二択分岐してみて大きい方で解けなかった場合は小さい方のパターンで試してみます。
- もしも残りブロック数が5つ以上あり明確な差が生じなかった場合は「濃い」「薄い」で「 4.仮置きしたマス目以外は解けない 」個数が少ない方で「1」ではない半分以上解けた時の配置を選び二択分岐をします。
- 残りブロック数が4つ以下の場合はどちらかを
- 二択分岐してみて少ない方で解けなかった場合は多い方のパターンで試してみます。
経験則によるもので数学的に説明できる法則ではありませんが、必ずそうなる訳ではありませんが「割と良く当たる」認識です。
なお、これまた経験上、この二択分岐をして両方とも手詰まりになる場合は、「連鎖がユニークになっていない」ケースか「どこかに手違いがある」ケースになると思いますので、まずは見直していただければ幸いです。
言葉の説明だけでは解り難いと思いますので数字「8」「4」「7」で試して行きます。
①数字「8」を調べる
どのような順番で数字を置いて行っても良いのですが、抜け漏れやダブりが無いように今回は一番左の列の一番上の行から縦方向で順番に置いて行きます。
ピンク色の数字が数字を置いた場所になります。
それが置かれることで解法その1から赤い数字のマス目が求められる事になります。

第4ブロック上→第6ブロック→第5ブロック
カウントは「薄い」1

第4ブロック下→第5ブロック→第6ブロック
カウントは「濃い」1
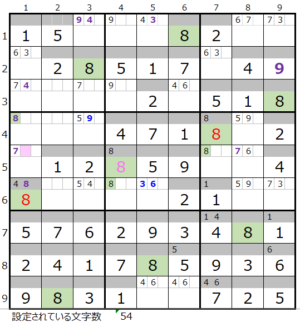
第5ブロック上→第6ブロック→第4ブロック
カウントは「濃い」1
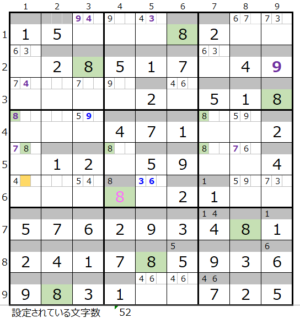
第5ブロック下
カウントは無し
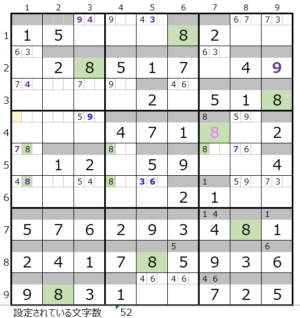
第6ブロック上
カウントは無し
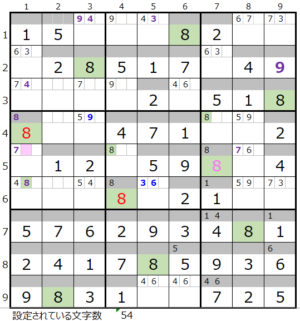
第6ブロック下→第5ブロック→第4ブロック
カウントは「薄い」1
以上により、カウントの結果としては
・濃い—1,1
・薄い—1,1
で差が無くまた、「 仮置きしたマス目以外は解けない 」個数も
・濃い—1つ
・薄い—1つ
となり、「濃い」「薄い」で差が無い結果になります。
このように残り3ブロックの場合は、有効な結果を得ることができない認識ですので、よほど数字が置かれる事で他の数字の解決につながらない限りは後回しにするのが得策です。
②数字「4」を調べる
数字「4」は残り4ブロックですので試して見る価値はあります。
なお4ブロックですので2ブロック以上がカウントする対象になります。
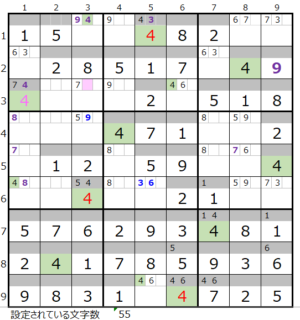
第1ブロック→第4ブロック→第2ブロック→第8ブロック
カウントは「薄い」1
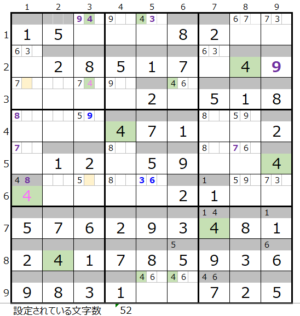
第4ブロック
カウントは無し
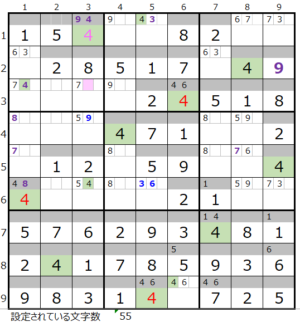
第1ブロック→第4ブロック→第2ブロック→第8ブロック
カウントは「濃い」1
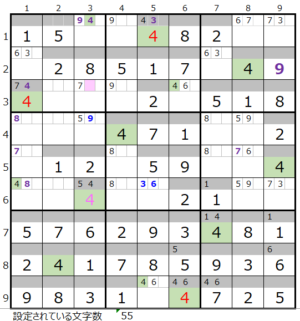
第4ブロック→第1ブロック→第2ブロック→第8ブロック
カウントは「薄い」1
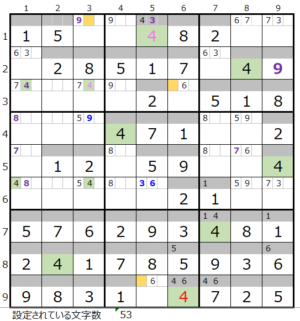
第2ブロック→第8ブロック
カウントは「薄い」1/2
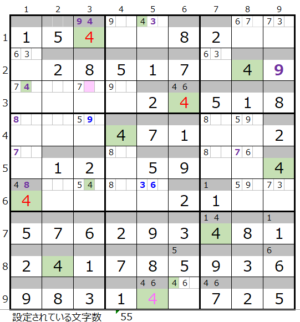
第8ブロック→第2ブロック→第1ブロック→第4ブロック
カウントは「濃い」1
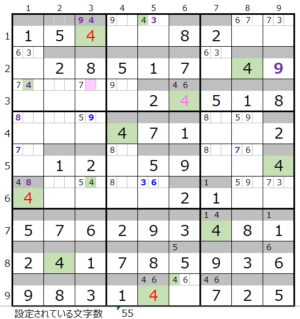
第2ブロック→第8ブロック→第1ブロック→第4ブロック
カウントは「濃い」1
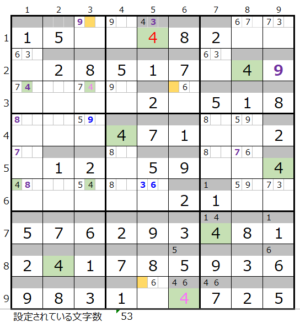
第8ブロック→第2ブロック
カウントは「薄い」1/2
以上により、カウントの結果としては
・濃い—1,1,1
・薄い—1,1,1/2,1/2
となり、「濃い」「薄い」でカウントの合計に差がありませんでした。
なお残りブロック数は4つのため、「 仮置きしたマス目以外は解けない 」個数は有効ではないので、 まずは「濃い」バターンから二択分岐をしてみます。
なぜなら「濃い」パターンはカウントがすべて「1」なので二択分岐をする上では都合が良いからです。
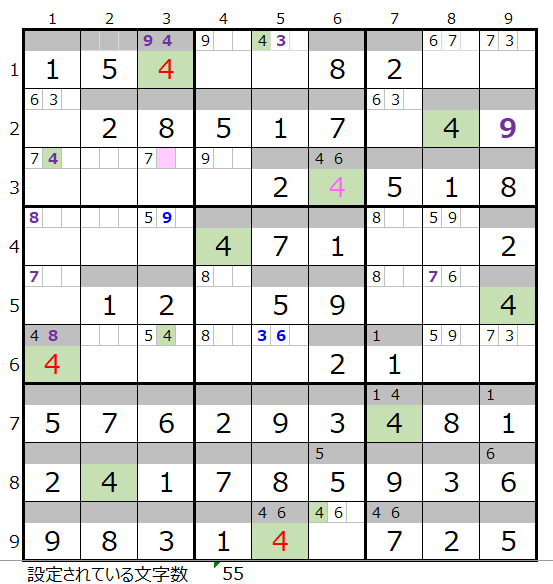
左図のように数字「4」がすべて埋ったところからスタートします。
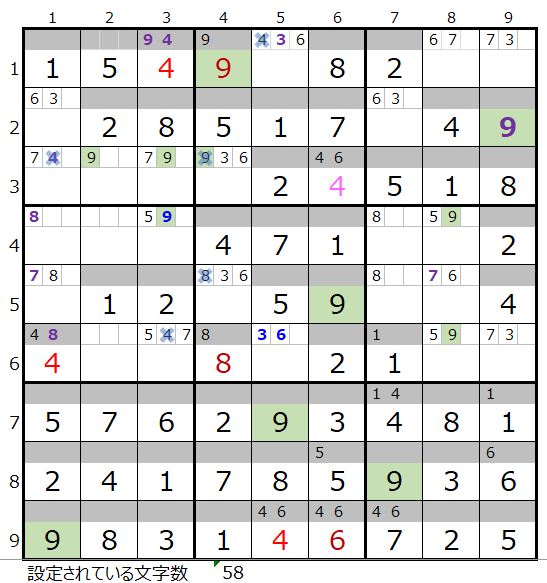
ただ残念ながら途中で行き詰まってしまいます。
不正解ではありませんが…..
このような場合の対処法としては下記の2つになる認識です。
- 数字の「4」以外に候補となる数字が無いか?確認して、なければ二択分岐する
- 残りが少ないのでここで仮置きをして先読みする
「仮置きして先読みする」ことと「二択分岐する」こととで何か違いがあるか?というとやる事は同じになりますが、例えば左図では「3」「6」が6ヶ所あるのでまずはどちらかで確認して見るのも一考です。
②数字「7」を調べる
数字「7」は残り4ブロックで先ほどの数字「4」と同じです。
4ブロックですので2ブロック以上がカウントする対象になります。
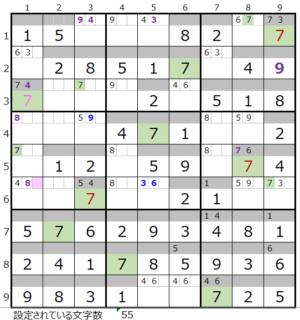
第1ブロック左→第4ブロック→第6ブロック→第3ブロック
カウントは「薄い」1
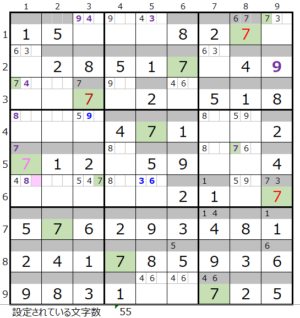
第4ブロック左→第6ブロック→第3ブロック→第1ブロック
カウントは「濃い」1
※第6ブロック真ん中列の上下メモ欄が「5,9」で確定しているために第6ブロックが成立する。
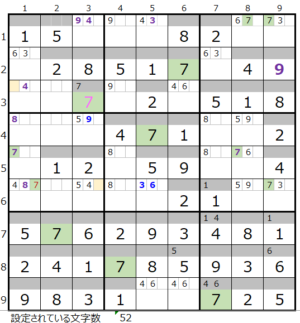
第1ブロック右
カウントは無し
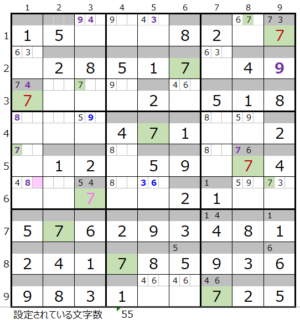
第4ブロック右→第1ブロック→第3ブロック→第6ブロック
カウントは「薄い」1
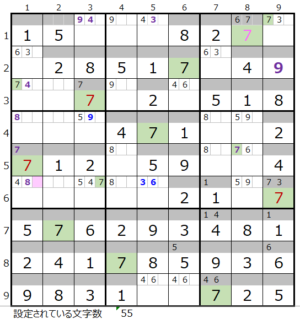
第3ブロック左→第6ブロック→第4ブロック→第8ブロック
カウントは「濃い」1
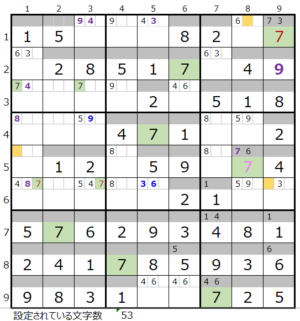
第6ブロック左→第3ブロック
カウントは「薄い」1/2
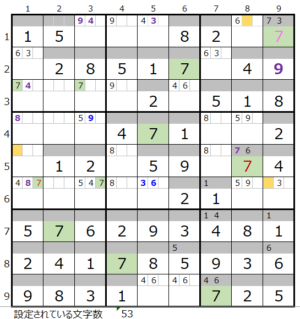
第3ブロック右→第6ブロック
カウントは「薄い」1/2
※第6ブロック真ん中列の上下メモ欄が「5,9」で確定しているために第6ブロックが成立する。
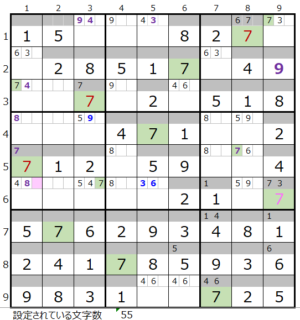
第6ブロック右→第3ブロック→第4ブロック→第1ブロック
カウントは「濃い」1
以上により、カウントの結果としては
・濃い—1,1,1
・薄い—1,1,1/2,1/2
となり、「濃い」「薄い」でカウントの合計に差がありませんでした。
なお残りブロック数は4つのため、「 仮置きしたマス目以外は解けない 」個数は有効ではないので、 まずは「濃い」バターンから二択分岐をしてみます。
理由は「4」の場合と同様に「濃い」パターンはカウントがすべて「1」のためです。
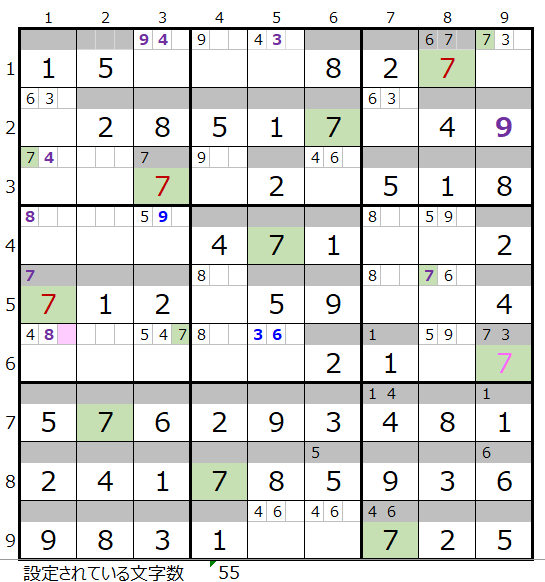
左図のように数字「7」がすべて埋ったところからスタートします。
是非皆さまでも一度ご確認いただきたのですが、残念ながらこの場合は手詰まり、つまり不正解となります。
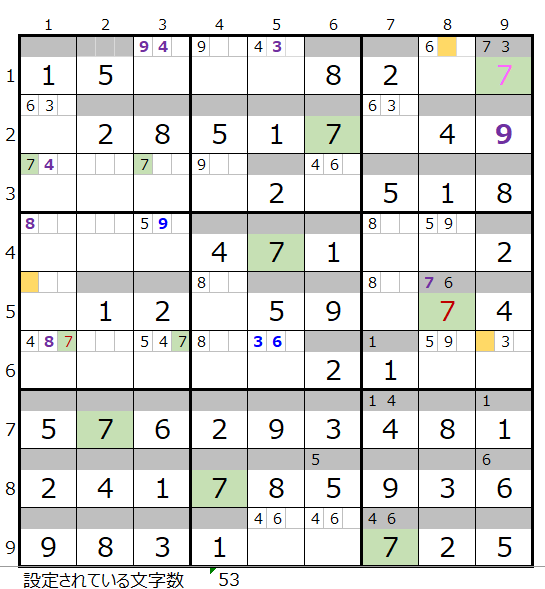
そうなりますと、二択の残りである「薄い」場合で確認する事になますが、「薄い」は半分以上のケースがありますので左図の盤面からスタートします。
結果につきましては、是非皆さまでご確認をいただけ貼れば幸いです。
まとめ
解法その4では取り合えず言わば強引に連鎖を決めてしまうのに対し「色分けの手法」は、ユニークな連鎖を見つけ出すことで二択分岐を全面的に使わずに正解にたどり着く可能性がある点であると考えています。
ただし手法としてはロジカルに数字を求めるものではなく実際に試して見た結果を評価するという「経験値に基づく状況分析」を行う手法なので、数独の解法としては成立しないものかもしれません。
ロジカルに解ず状況分析に頼る理由としては、本解法が「メモ欄にセットするのは、基本狙い目2つまで」にしていることのに起因する認識です。
しかしながらこの「基本方針」を見直すとなると相当な時間がかかると考えており、いまいまそれをせずに二択分岐を減らすため導き出した苦肉の策であることは確かです。
なおもう少しいくつかの事例をご紹介しないと「たまたま成立しているのではないか?」と思われることと存じます。
そこで次回は残り5ブロックでのケースをご紹介したく存じます。
以上、最後までご一読いただきありがとうございました。

