これまで14回に渡り「解法その1」~「解法その4」そして「色分けの手法」をご説明して来ましたが、第15回からその後数回に渡り最終回として、第1回の時にご紹介した「世界一難しい数独」の問題に「色分けの手法」を使って再度ご説明しています。
今回はその4回目になります。
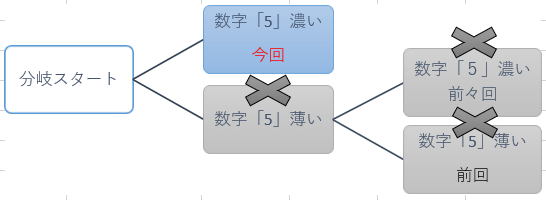
前回までは、最初の盤面から数字「5」で「濃い」「薄い」の二択分岐をした時の「薄い」方のその先をご説明して来ましたが、今回からはもう片方の分岐の「濃い」場合について2回に渡りご説明して行きます。
今回の説明で使用する数独問題について
第1回の時にもご紹介していますが、今回の問題は2012/7/3日付の「ロケットニュース24」に掲載されている「世界一難しい数独」になります。
一回目の二択分岐その2『「濃い」「5」』で仮置きをした盤面
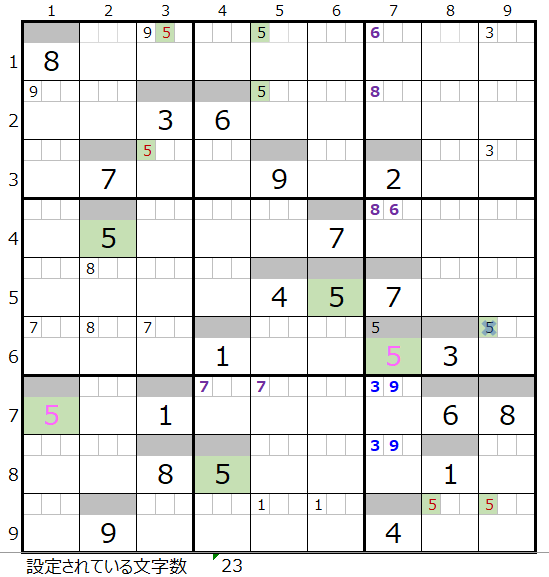
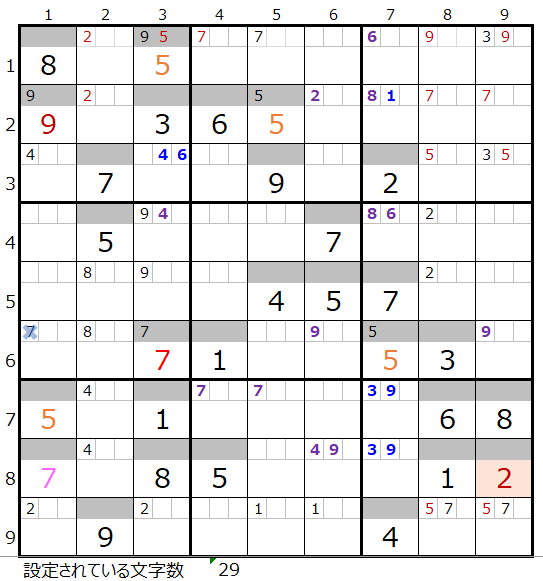
この盤面は第15回「世界一難しい数独その1」で分岐のご説明をした後の続きになりますが、文字数は23文字になっています。
本解法その1から3では盤面として行き詰まった状態です。
左図のメモ欄
・黒字茶字—解法その1からセット
・紫太字—解法その2からセット
・太青—解法その3からセット
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 20 | 43 | 23 | 31 | 6 | 28 | 16 | 16 | 21 |
既に一度仮置きをしている数字「5」が6ヶ所で一番少ないのですが、同じ数字だけを攻めてもバランスが悪いので次に少ない数字を先に調べて見ます。
置ける場所の数が少ない数字で複数連鎖を考える
結果を見渡すと数が少ないのは数字「5」の6ヶ所で、その後は「7」の16か所、「8」の16ヶ所、になります。
ただし実際に試して見ると(盤面は省略いたしますが)残念ながら数字「7」と「8」ともに複数連鎖の対処法では「濃い」「薄い」でそれぞれ2つ以上共通して通過するマス目が存在していませんでした。
という事で、今回も数字「5」を再度考える事にします。
数字「5」で再度連鎖を考える
ほぼほぼメモ欄に情報がありますので、第3ブロックをどのように通過するか?を考えることになることと存じます。
なお漏れなく連鎖を見つけ出すためには、まず一つ連鎖を見つけて、対角で置き換え可能なポイントを探して確認して行くのが良い認識です。
今回の場合は置き換え可能なポイントは1ヶ所になります。
また置き換えをすることで新たに見えてくる置き換え可能なポイントはありませんでした。
最終的に「成立」する連鎖はつぎの2つになることが解ります。
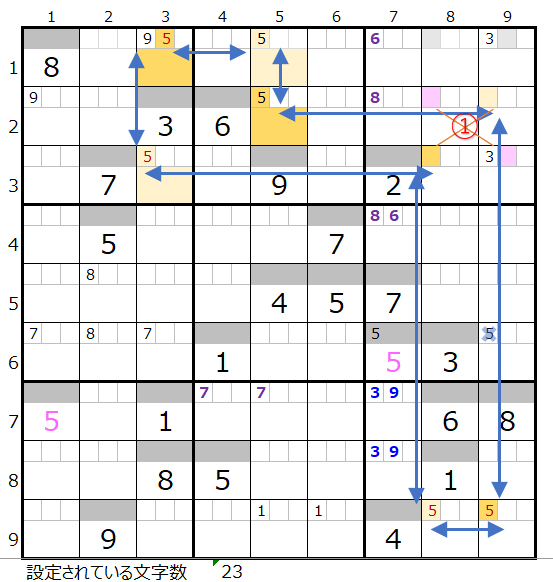

なお共通して通過するマス目は「濃い」「薄い」背景色を付けた2か所づつとなります。
これらのマス目の中には「スクウェアになり得る箇所」は存在していませんのでそれぞれの箇所に「5」を仮置きして二択分岐で解き進めるて行きます。
ただし解法その1からその3だけでは「濃い」「薄い」ともにそれぞれ下図の盤面で行き詰まることが解ります。
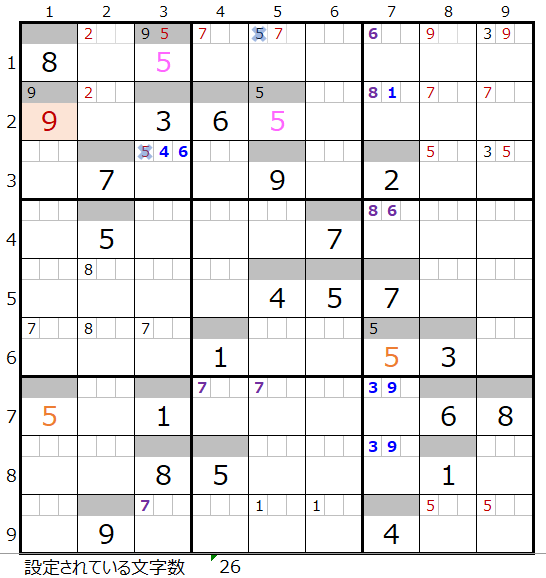
「濃い」方は背景色を付けた「6」が決まります。
まずはこちらの「濃い」方の分岐を次の章以降でご説明致します。
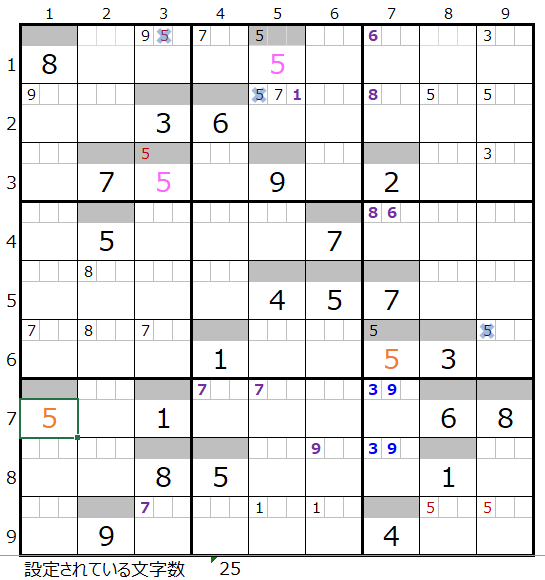
「薄い」方はメモ欄に情報が追加されるだけで数字の解決はありません。
こちらの「薄い」方の分岐につきましては次回ご説明をいたします。
二回目の二択分岐その1『「濃い」「5」』での盤面

この章でご説明するのは左図2つ目の数字「5」「濃い」の場合です。
数字「5」「薄い」につきましては次回ご説明致します。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 17 | 34 | 23 | 28 | 0 | 26 | 5 | 15 | 14 |
「0ヶ所」の数字「5」で二択分岐することは可能ですが、今回は0を除き一番数が少ない数字「7」を確認して見ることにします。
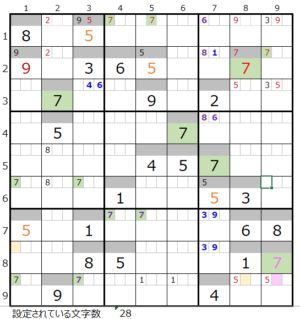
数字「7」で連鎖を考える
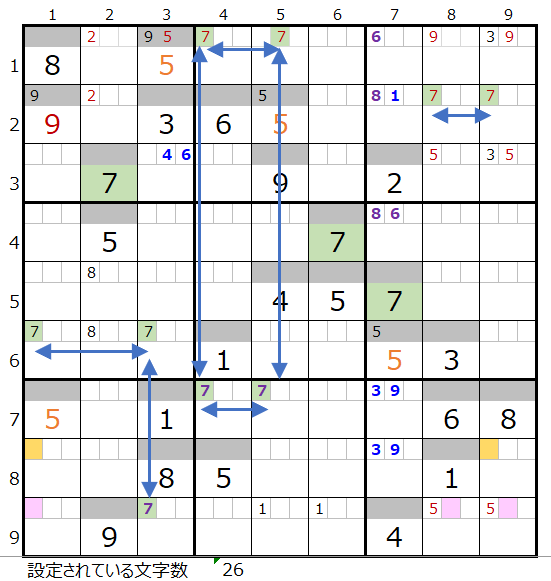
数字「7」は第2ブロックは解法その1から、第8ブロックは解法その2からメモ欄にセットされた情報から左図中央の紺矢印のスクウェアができることが解ります。
となると、残り4ブロックをつなぐ連鎖を考える事になるのですが、8行目のメモ欄背景色オレンジ色のところは2か所で他に薄ピンク色のところはないので、この2か所は必ず通ることを表しています。
となるとほぼほぼ連鎖が見えてくることになることと存じます。
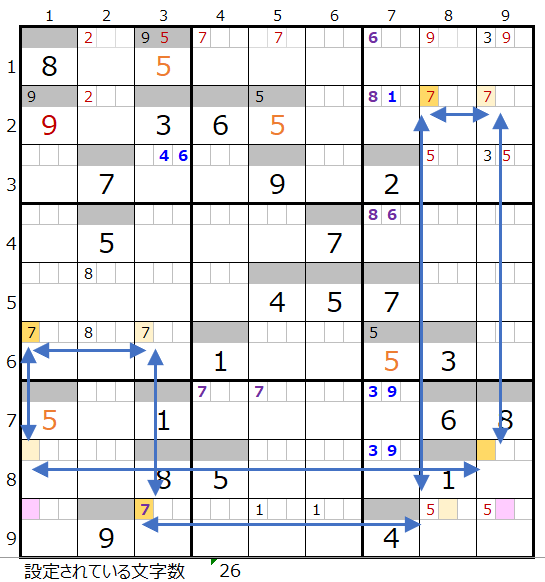
実際に確認して見ると、左図のような色分けの正しい連鎖がある事が解ります。
しかもありがたい事に、これ以外には残りの4ブロックをつなぐ連鎖は存在しないユニークな連鎖となるので「色分の正誤を判断するための手法」を使用することができます。
「色分けの手法」の内容につきましては本シリーズの第10回から第12回をご参照いただければ幸いです。
なお残り4ブロックになりますので、「 仮置きしたマス目以外は解けない 」個数は有効ではありません。
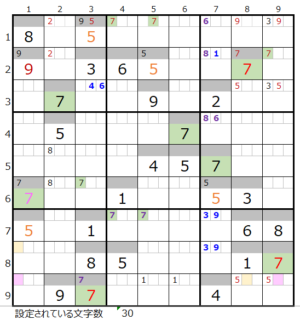
①第4ブロック→第7ブロック→第9ブロック→第3ブロック
カウントは「濃い」1
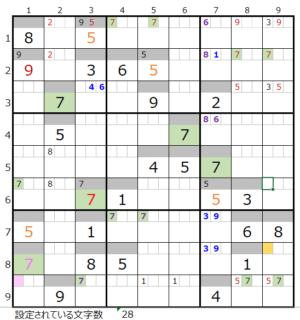
②第7ブロック→第4ブロック
カウントは「薄い」1/2
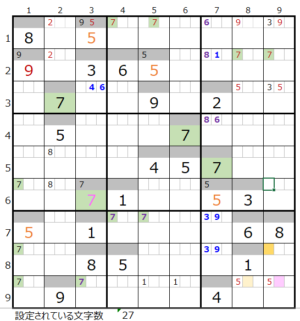
③第4ブロック
カウントは無し

④第7ブロック→第4ブロック→第9ブロック→第3ブロック
カウントは「濃い」1
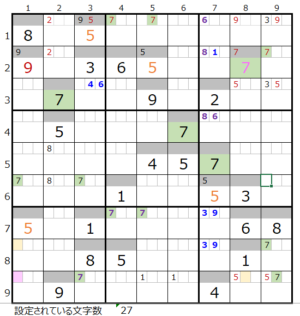
⑤第3ブロック
カウントは無し

⑥第9ブロック→第3ブロック→第7ブロック→第4ブロック
カウントは「薄い」1

⑦第3ブロック→第9ブロック→第7ブロック→第4ブロック
カウントは「薄い」1
⑧第9ブロック→第3ブロック
カウントは「濃い」1/2
以上により、カウントの結果としては
・濃い—1,1,1/2
・薄い—1,1,1/2
となり、「濃い」「薄い」が同数となり残念ながら両方とも確認する必要があります。
「色分けの手法」の経験則に従い「濃い」1/2、「薄い」1/2で二択分岐することになります。
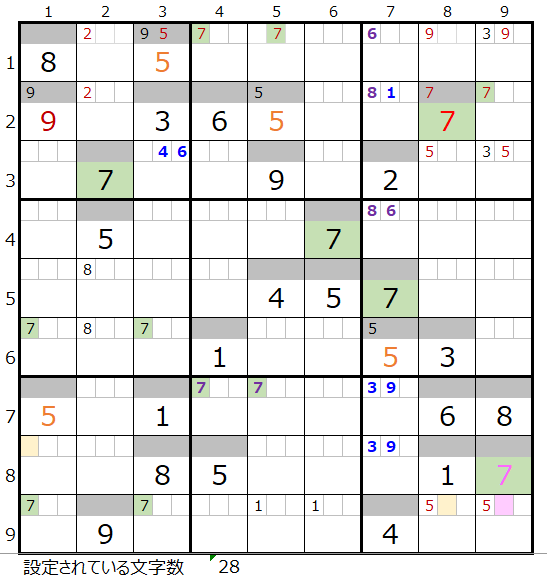
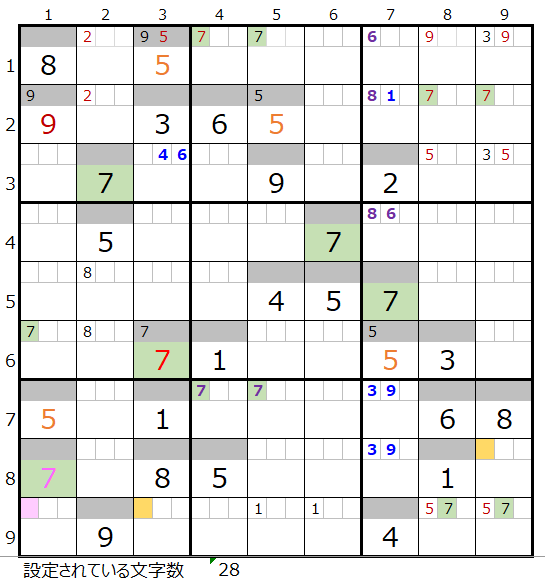
両者を解き進めるとそれぞれ1ヶ所数字が確定しますが下記盤面となり、解法その1からその3では両者とも行き詰まった状態になります。
・背景色の付いているマス目が解決したところです。
・なおメモ欄につきましては背景色は省略しています。
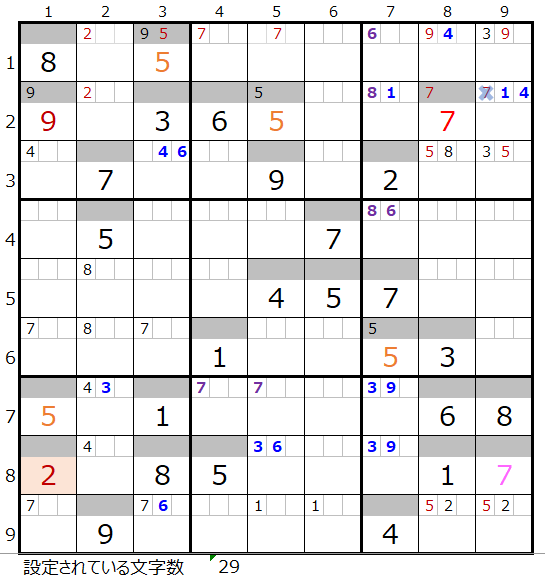
この後の章で、まず「濃い」場合のその先を確認し、さらに後段で「薄い」場合を確認して行きます。
三回目の二択分岐その1「濃い」「7」での盤面
この章でご説明するのは左図数字「7」濃いの場合です。
数字「7」薄いにつきましては後段でご説明致します。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 16 | 22 | 20 | 14 | 0 | 23 | 0 | 13 | 14 |
数字「8」が13か所でゼロを除いて一番少なくなるので「8」を選択します。
数字「8」で連鎖を考える

上左図2行目のメモ欄で背景色オレンジ色のところは、その行で2ヶ所しか置き場所がないので通過が確定しています。
数が多いので少し難しいですが第8ブロックを通過する事を考えるとルートが絞られてくるはずです。
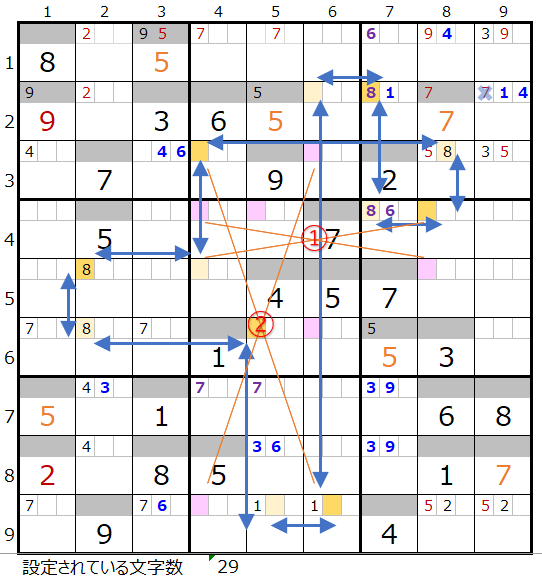
上右図のように色分も正しい連鎖がひとつ見つかりました。
なお対角で置き換えが可能なポイントは2ヶ所(①と②)あることが解ります。
この後、対角で置き換え可能なポイント①と②を順番に確認して行きます。
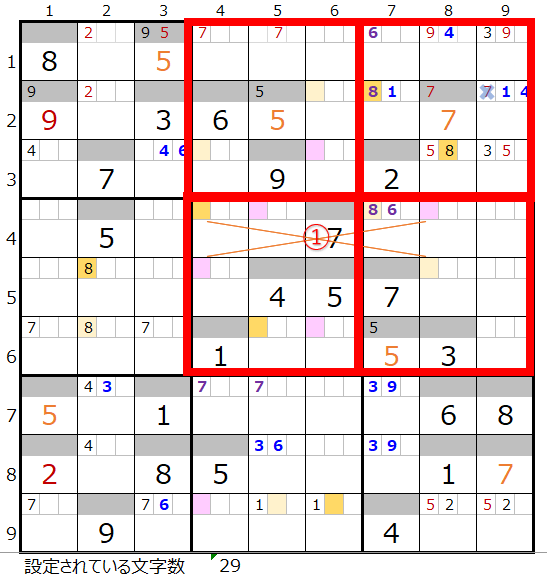
①の置き換えは上左図赤枠のブロックの色分けが正しくないため不成立となります。
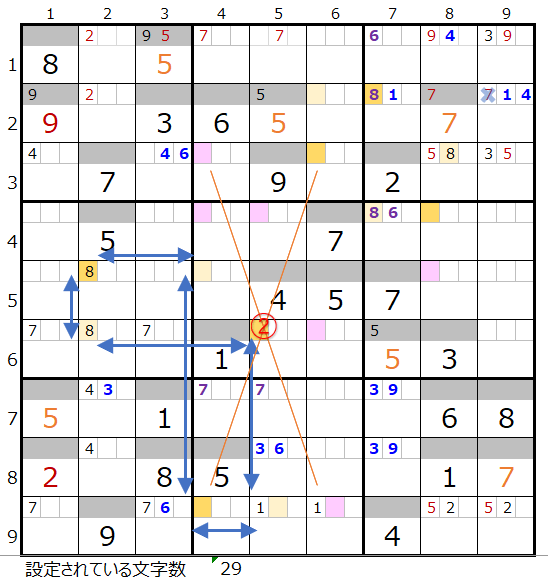
②の置き換えは上右図のように別ループができるため対象外となります。
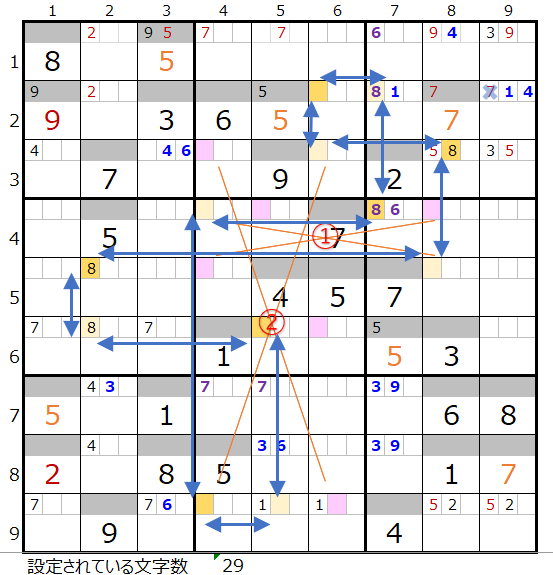
①と②同時に置き換えだ場合は左図のように色分けが正しい、残り全てのブロックを通過する連鎖ができることが解ります。
以上の確認した3つのバターンには新たな置き換えポイントは見つかりませんでした。
そこで、成立した2つの連鎖で共通して通過するマス目を調べて行きます。
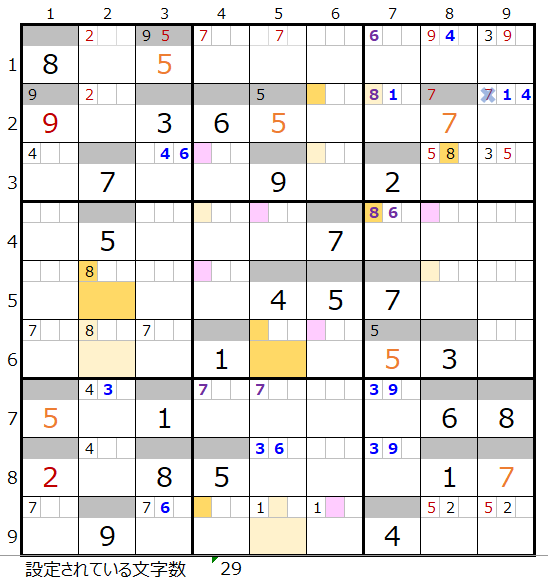
共通して通過するマス目は「濃い」「薄い」の背景色付けたそれぞれ2ヶ所づづとなります。
この中にはスクウェアになり得る箇所はないので、「濃い」「薄い」で数字「8」を仮置きして二択分岐をすることになります。
「濃い」「薄い」で仮置きした盤面はそれぞれ下記になります。
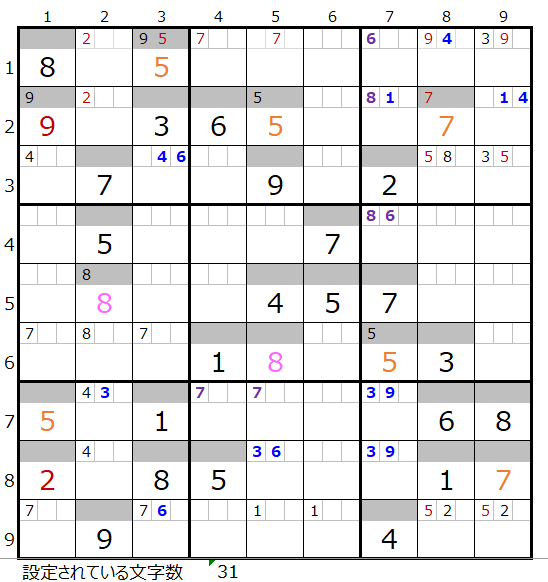
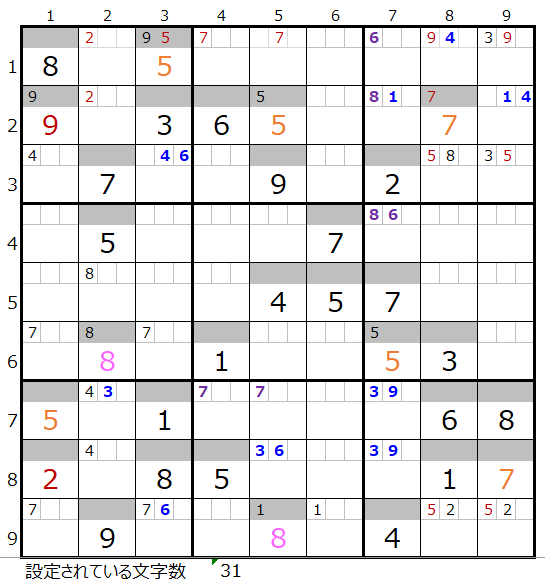
両者を解き進めるとそれぞれ下記の盤面になります。
残念ながら両者ともに途中で手詰まり(解けない)という結果になります。

第5ブロックに数字「6」が入らない事が解ります。
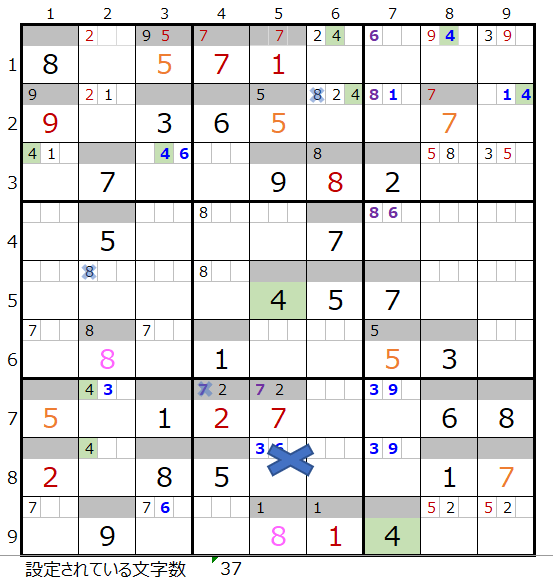
第8ブロックに数字「4」が入らない事が解ります。
以上の結果から、『三回目の二択分岐その1「濃い」「7」』の分岐には正解が無い事が解りました。
続けて、残っているもう片方の『三回目の二択分岐その1「薄い」「7」』を調べて行きます。
三回目の二択分岐その2「薄い」「7」での盤面
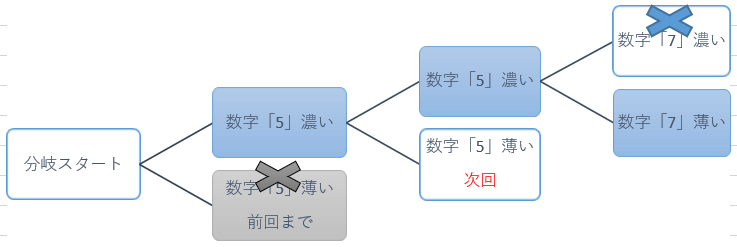
『数字「7」濃い』には正解が無い事が解りましたので、この章では三回目の二択分岐その2として『数字「7」薄い』を見て行く事にします。
メモ欄で該当する数字が置ける場所を確認する
(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 17 | 16 | 22 | 14 | 0 | 24 | 0 | 15 | 8 |
ゼロを除くと数字「9」が8か所になるのでまず最初に「9」を選択しますが、数字「9」が上手くいかない場合は次に少ない数字「4」を試して行きます。
①数字「9」で連鎖を考える
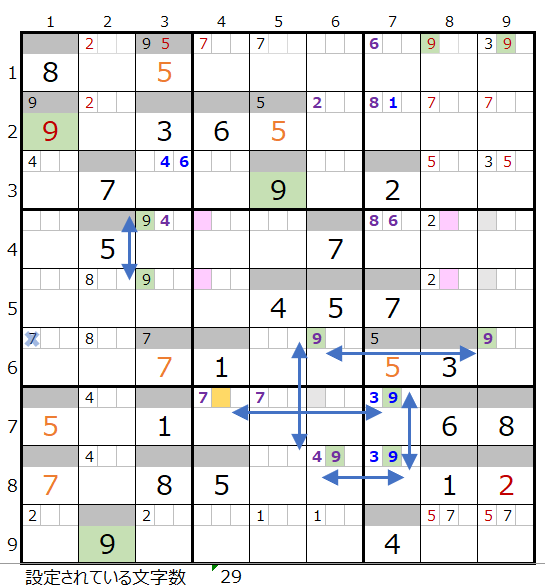
メモ欄にセットされた数字で紐づけできるところを結ぶと上左図のようになります。
6列目の1ヶ所と9列目の2ヶ所で背景色灰色のところは既にその列で2か所置き場所が決まっているためにそれ以上置くことができないことを表しています。
7行目の背景色オレンジ色のところは上記により置き場所が2ヶ所となり必ず通過する事を表しています。
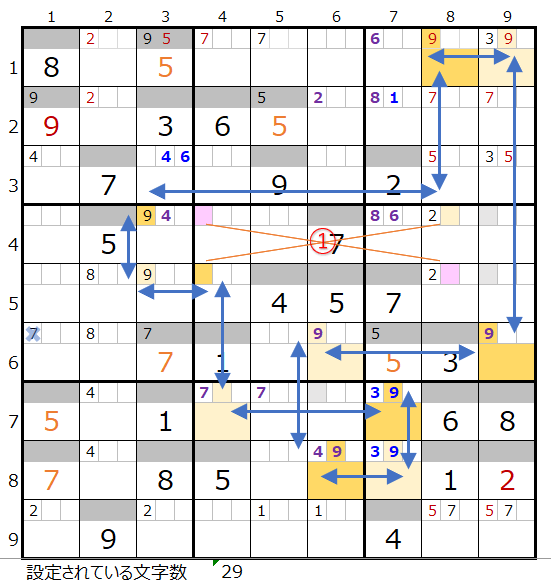
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換え可能なポイントは1ヶ所(①)になります。
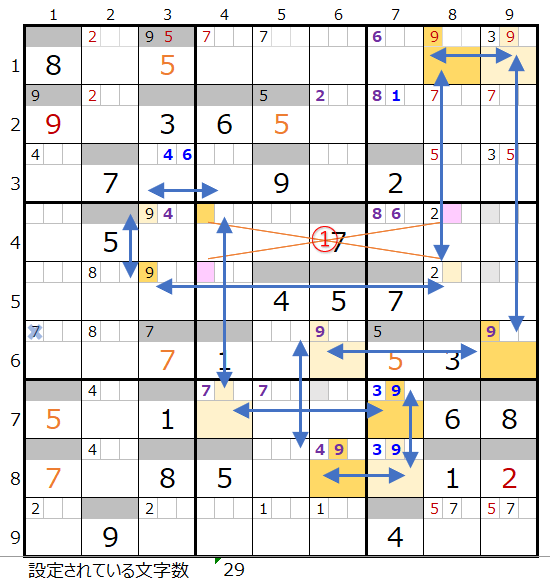
①を置き換えて見ると、上左図のようにもう一つの連鎖が成立することが解ります。
またこれ以上の残り全てのブロックを通過する連鎖は存在しない認識です。
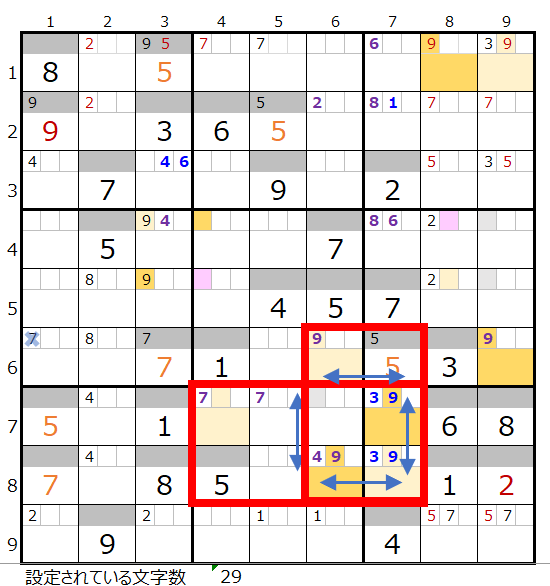
2つの連鎖で共通して通過するマス目に「濃い」「薄い」で背景色を付けると上右図のようになります。
ただし赤枠の2ヶ所はスクウェアになり得る箇所となるために、経験則としては数字「9」はあきらめることになります。
なお「おきて破りの方法」として赤枠の部分を除外するやり方もありますが、そうすると「薄い」は1ヶ所となってしまうためわざわざこの方法を採用するまでもない状況です。
そうなると、次に数の少ない数字「4」(14ヶ所)を確認して見ます。
②数字「4」の連鎖を考える
第1候補の数字「9」を採用する事ができなかったので、第2候補の数字「4」を確かめてみる事にします。
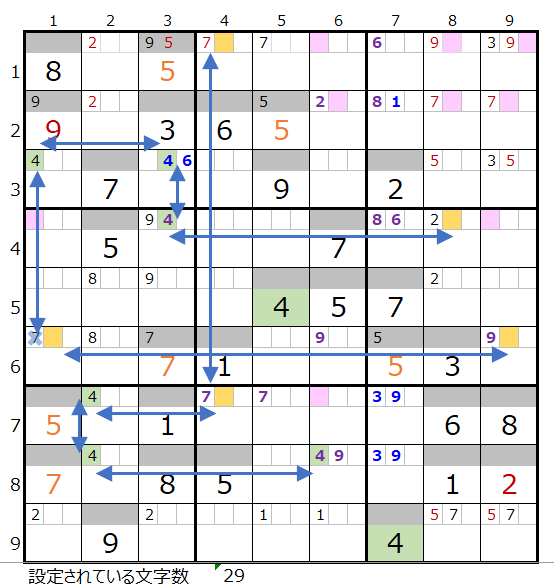
残り7ブロックのケースで少し難しいですが、縦方向、横方向で2ヶ所しか置けないところ(上左図の背景色オレンジ色のところ)が見つかりますので、その情報をもとに連鎖を絞り込んで行きます。
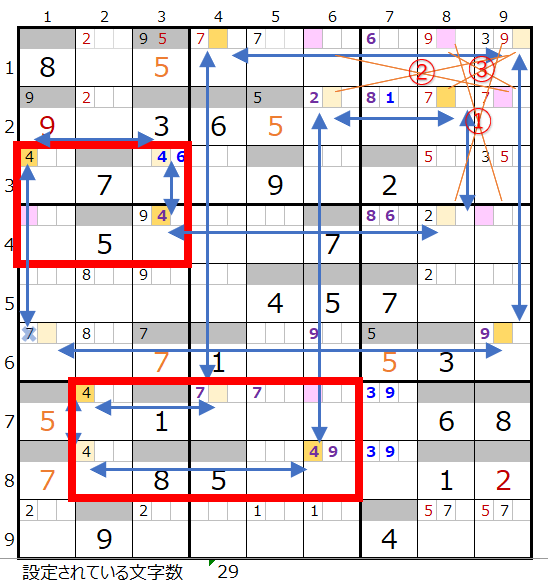
そうすると上右図のような色分けが正しい連鎖が見つかります。
ただし対角で置き換え可能なポイントが3ヶ所右上のところに固まっていて、赤枠の2ヶ所は共通して通過するマス目になりそうなのですが、この形は先ほどの数字「9」と同様なスクウェアになる箇所を含んでいるため採用できない危険性があります。
という事は数字「4」も採用できないことになります。
そうなると残された数の少ない数字の候補としては
・数字「8」—15か所
・数字「2」—16か所
・数字「1」—17か所
となりますが、確認すると対角で置き換え可能なポイントや置き換えることで新たに見つかる置き換えポイントが多くあるために、「濃い」「薄い」それぞれ2ヶ所以上共通して通過するマス目は存在しないことが解ります。
全ての候補が採用できないとなると、残されているのはゼロになっている数字「5」か「7」のいづれかになります。
どちらもスクウェアの形ですが、第9ブロック9行目のメモ欄は数字「5」と「7」と被っているので、数字「5」を選択して二択分岐することにします。
③四回目の二択分岐「5」「右上がり」「右下がり」
結果論にはなりますが今回の場合は「色分けの手法」を深追いせずに二択分岐に切り替えた方が良かったのだと思います。
数字「5」を仮置きした盤面はそれぞれ下記になります。
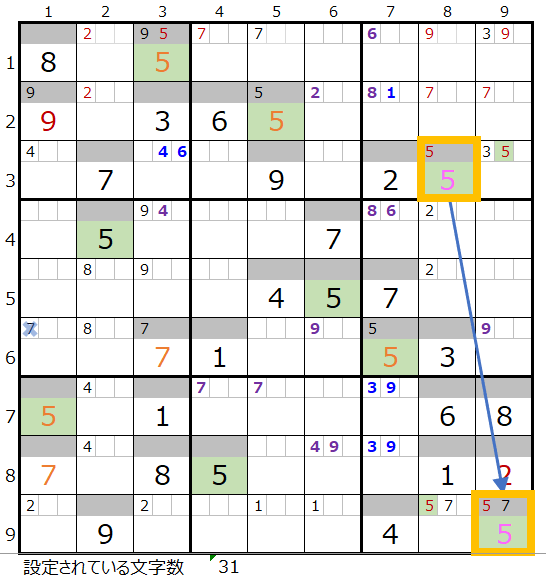
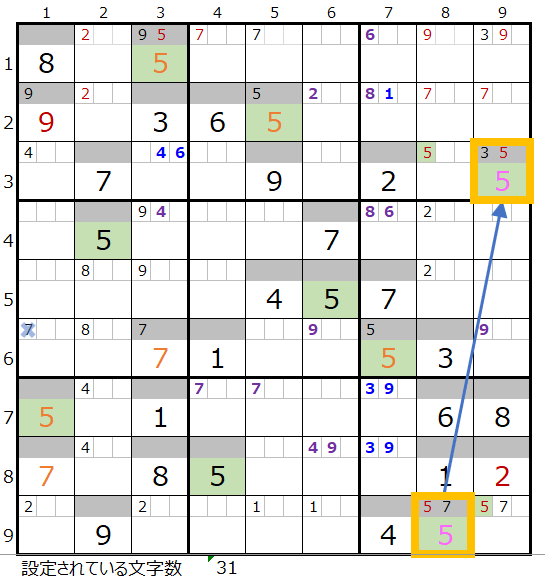
両者を解き進めるとそれぞれ下記盤面になります。
「右上がり」につきましては途中で手詰まり(解けない)という結果になりますが、「右下がり」は行き詰まった状態になります。
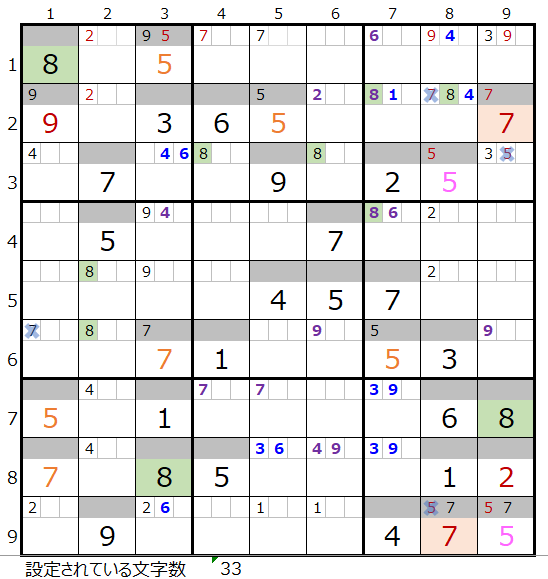
解法その1から3では上右図まで解き進める事ができますが、これ以上は解き進めることができません。
・背景色の付いているマス目が解決したところです。
・なおメモ欄につきましては背景色は省略しています。
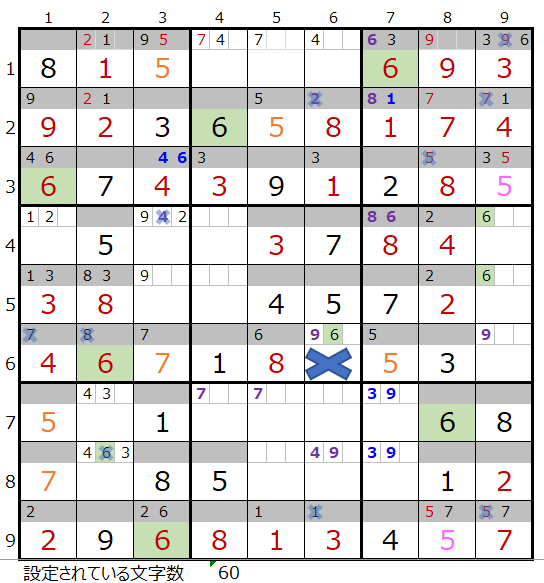
第5ブロックに数字「6」が入らない事が解ります
この後「右下がり」につきまして更に解き進めて参ります。
四回目の二択分岐「5」「右下がり」での盤面
『数字「5」右上がり』には正解が無い事が解りましたが、「右下がり」はまだ確定していないので引き続き解き進めて行きます。
メモ欄で該当する数字が置ける場所を確認する
(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 16 | 16 | 21 | 11 | 0 | 22 | 0 | 10 | 8 |
数字「9」の8か所は先ほどと変わらないため盤面が動いても「スクウェアになり得る箇所」が残っている事が想定されるので、次に数が少ない数字「8」(10ヶ所)について調べる事にします。
数字「8」で連鎖を考える
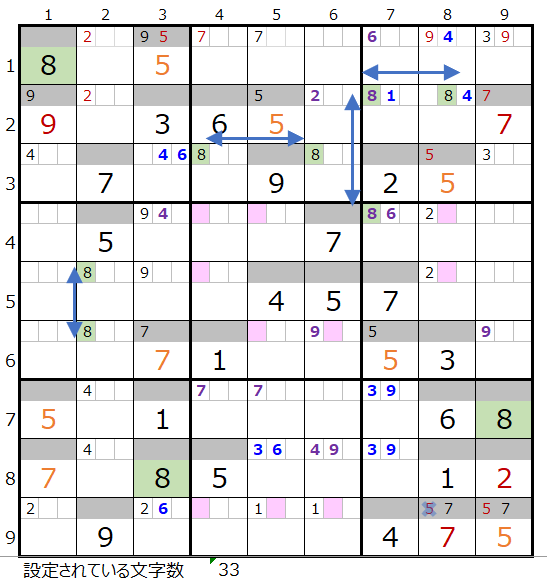
メモ欄にセットされた数字で紐づけできるところを結ぶと上左図のようになります。
第3ブロックを通過するためには第6ブロックから入る事になるので、残りをどのように通過するかを考えることになります。
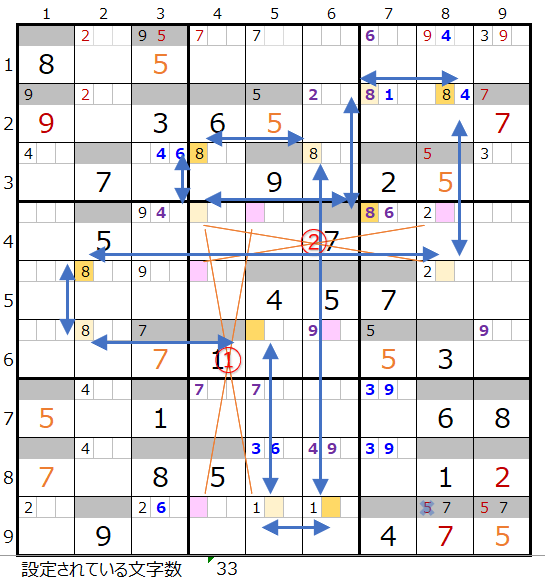
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換え可能なポイントは2ヶ所(①と②)になります。
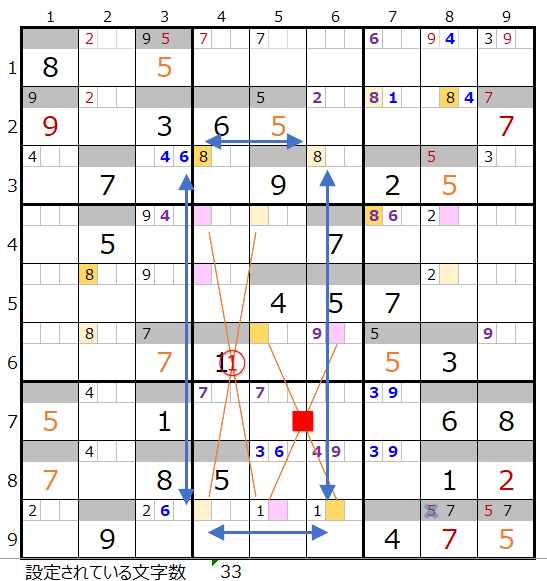
①を置き換えると上左図のようにスクウェアができるので対象外となります。
なお新たに置き換え可能な×■印が現れるので次にこれを確認します。
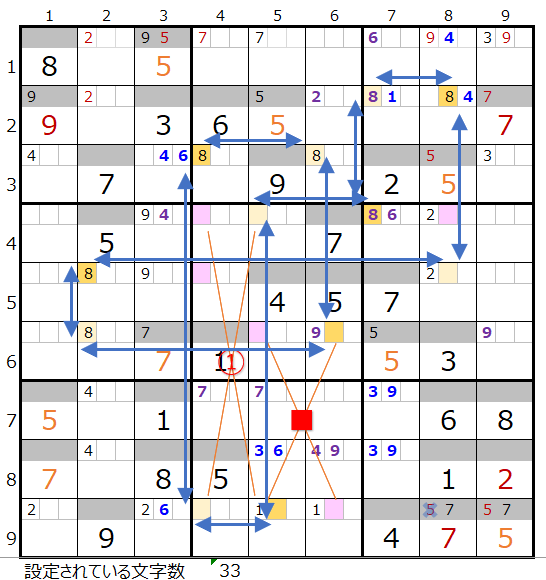
■を置き換えると上右図のように色分けが正しいもう一つの連鎖あることが解ります。
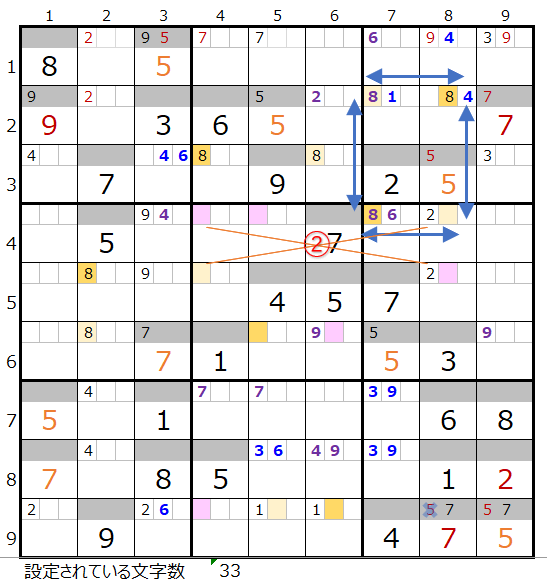
最後に②を置き換えると上左図のようにスクウェアができるので対象外となります。
これには新たに置き換え可能なポイントは無いので連鎖は2つであることが解ります。
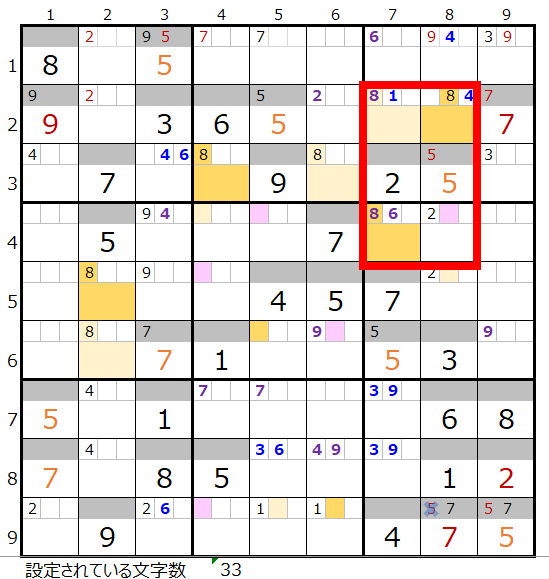
共通して通過するマス目は「濃い」「薄い」の背景色付けた「濃い」4ヶ所と「薄い」3ヶ所になります。
ただしこの中にはスクウェアになり得る箇所が赤枠のところにあるので、「おきて破り」にはなりますが、赤枠のところの3ヶ所を除外して二択分岐することにします。
両者を解き進めるとそれぞれ下記盤面になります。
残念ながら両者ともに途中で手詰まり(解けない)という結果になります。
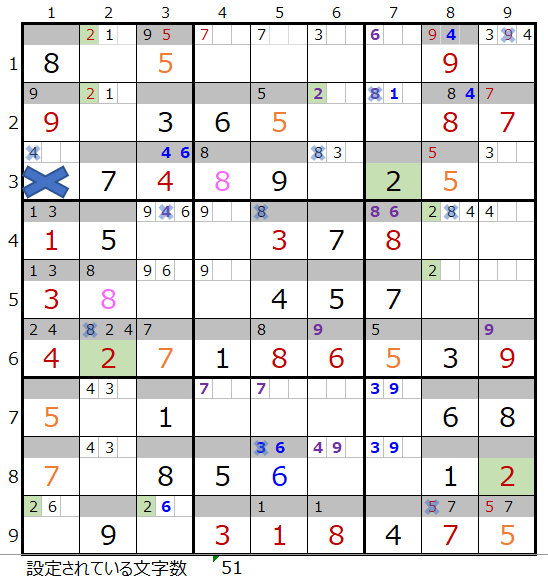
第1ブロックに数字「2」が入らない事が解ります。

第2ブロックに数字「7」が入らない事が解ります。
なお解き終わった盤面でのご説明となり恐縮ですが、黄枠の数字「4」は青枠の「4」が決まったことから縦方向の解法その2からセットされています。
またその右隣の「3」は解法その3からセットされています。
以上の結果から、『四回目の二択分岐「5」「右下がり」』にも正解は無く、『三回目の二択分岐その1「薄い」「7」』の分岐には正解が無い事が解りました。
そうなりますと、今回確認した『二回目の二択分岐その1「薄い」「5」』の分岐には正解が無い事になります。
まとめ
今回は数字「5」での二回目の二択分岐で「濃い」場合のルートを最後までご説明いたしましたが、残念ながらこの分岐には正解が無い事が解りました。
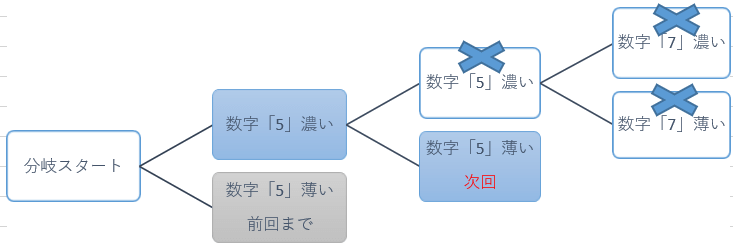
次回はいよいよ最後となりますが、二回目の分岐『数字「5」「薄い」』ルートのその先についてご説明したく存じます。
最後までご一読いただき誠にありがとうございました。