前回の第9回目で「二択分岐による解法」をご説明いたしましたが、その中で「組み合わせの整合性を確認する事で解法につながるか?」という課題を残していました。
第9回目から約3ヶ月が経ちますが、その間に上記の課題への対応とともに「二択分岐はなるべく使わない形で解けないか?」という検証作業を進めて参りました。
その中で「組み合わせの整合性を確認する」ことである程度の有効性を確認する事ができましたので「色分け手法」としてご説明をしたく存じます。
そもそも書式まで作っておきながら「なぜ二択分岐を使用しない方法を模索するのか?」なのですが、それは二択分岐では解けないパターンを解いた時に皆様が感じるであろう「虚無感」と「手戻り感」を「何とかしたい」という思いからになります。
今回ご紹介する「色分け手法」ですが、メモ欄にセット数字の縦・横・ブロックでの並びの整合性を確認する手法となります。
ただし、「並びの整合性」や「マス目のメモ欄にセットされている自分以外の数字との関係性」を調べるだけではなかなかマス目にセットする数字の特定までには至らない事が解りました。
特に「解法その3」まで進み、これ以上の手かがりが無くなった時点で盤面に置かれた数字の数が40前半以下の場合は、解法の糸口を見つけることができないケースが多くございます。
そこで、「整合性や関係性」以外に「状況分析」から「色分の正誤を判断するための手法」につきましても、合わせてご紹介いたします。
なお残念ながらこの手法を使ってもすべての数独の問題を解くことができるわけではありません。
今回の検証にあたり使用されていただきました下記サイトの2015年11月の問題集「数独問題集(達人級)」でも2割程度は本手法で解くことができませんでした。
従いまして「解けない問題は深追いせずに早めに二択分岐に切り替える事が寛容である」という認識です。
つきましては、この後数回に渡って具体的に問題の一部を使用させていただきながらご説明して行きたく存じます。
今回の説明で使用する数独問題について
今回は、前回の第9回で二択分岐での解法をご説明した問題を「色分け手法」を使用するとどのようになるか?をお示ししたく存じますので前回と同じく下記サイトの2015年11月の問題集の中の「数独問題集(達人級)」2015/11/18下段の問題を使ってご説明致します。
なお、コピーライトは問題を作られている数独無料問題集様がお持ちのものになりますので初期の盤面につきましては、上記サイトにてご確認いただけますようお願い申し上げます。
「解法その3」終了時の盤面
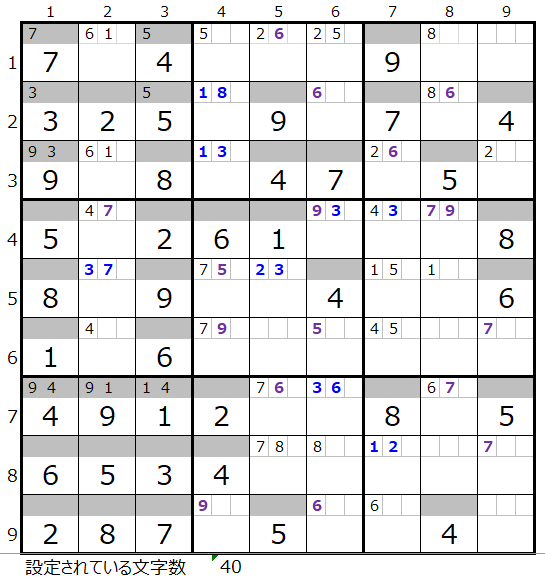
青色太字でメモ欄に記入されている数字が「解法その3」で得られた情報になりますが、盤面としては行き詰まった状態です。
※ちなみに、5行5列のマス目のメモ欄にセットされた「2,3」ですが数字の「7」は解法その1で、このブロックのメモ欄に「7」がセットされているのを使っています。
この盤面に対する前回の説明を引用
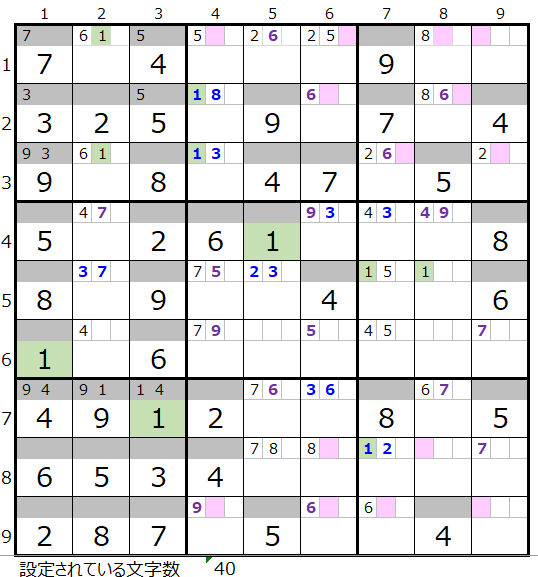
下記のイタリック文字の説明は前回の引用になります。
「解法その4」のためには設定されている文字数が40台後半にならないと、一般的には情報が足りない状態になります。
左図は数字の「1」で「解法その4」を試みた場合になります。
背景色薄ピンク色のメモ欄が「1」が入る可能性がある場所になるのですが、選択可能なパターンの数が多いので、絞り込むのは難しい状況です。
色分け手法とは
色分け手法は、解法その1からその3まで解き進めた時に、もうそれ以上どうすることもできない「行き詰った状態」になった時に使用する手法です。
メモ欄に横方向、縦方向で同じ数字が2つずつになるように、数字を埋めて行き数字の連鎖を見つけ出すところは、「解法その4」と同じです。なおこの時「一つのブロックに入る数字も2つ」になるように考慮する必要があります。
ただし「解法その4」と「色分け手法」との大きな違いは、「解法その4」はメモ欄にセットされている数字を頼りにして、まだ当該ブロックで該当数字が無く、メモ欄にも数字がセットされていない場所を探して数字を想定で埋めて行くのに対して、「色分け手法」ではターゲット(該当数字)がセットされていないブロックのメモ欄に対して、ターゲット(該当数字)がセット可能なすべてのマス目を洗い出して、そこから横方向、低方向で同じ数字を2つずつピックアップして数字の連鎖がいくつできるかを見つけ出す点です。
言葉だけでは上手く伝え切れない事と存じますので、上記の盤面を使いながら手順をご説明致します。
色分け手法の手順
前提
まずは、「解法その1~その3」により得た情報をメモ欄にセットします。
「解法その1~その3」だけでは手詰まりな状況になった時の盤面に設定されている文字数が40台前半以下の場合は、なかなか手強い問題になり「色分け手法」でも行き詰るケースはございます。
その場合は最終手段となる二択分岐に頼らざるを得ないのですが、どこで「できないと判断するか?」につきましては皆様の問題を解くことに対する熱量に依存していることと存じますが、あまり粘り過ぎて深追いし過ぎても良い結果が得られない場合もありますので、ほどほどにされることをお勧めいたします。
なぜそのような事をお勧めしているか?といいますと、このような行き詰まりになる原因は「本解法がメモ欄にセットする数字の個数を基本2つに限定している」ことによるものと推察しています。
従いまして、そもそも「本解法では二択分岐に頼らずに解くには限界がある」と認識しています。
なお、例えば「これを3つに増やした時にどのようになるのか?」につきましては現状は未検討の段階です。
そのためこれを調べて皆様にお伝えできるようになるには恐らく年単位での時間が必要になる事と存じます。
折を見て挑戦したいとは思っておりますので、長い目で見ていただければ幸いです。
①メモ欄にセットされている数字の状況を1~9すべて確認する
数字「1」状況は、本記事「この盤面に対する前回の説明」の見出しの画面キャプチャーにあるように、4ブロックに1が入る可能性のある背景色薄ピンク色が15か所あり、色分けの難易度としては高・中・低3段階で区別すると「高」になりますので、取り合えずそのままにしておきます。
なお難易度を可能性のある箇所の個数で決めるとすると目安としては下記のようになります。
ただし盤面に設定されている数字の数が少ない場合は全体的に個数がアップする傾向がありますのであくまでも目安として捉えていただければ幸いです。
| 難易度 | 可能性のある箇所の個数 |
| 高 | 10以上 |
| 中 | 5から9 |
| 艇 | 0から4 |
残りの数字に対して同様に調べて行くと小さな画面で恐縮ですが下記のようになります。
なお今回は説明のために可能性のある箇所の個数を数えていますが、ざっくりと難易度だけ把握すれば大丈夫です。
 2は9ヶ所
2は9ヶ所 5は1ヶ所
5は1ヶ所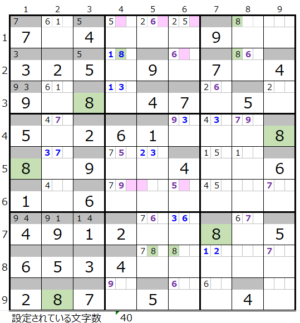 8は7ヶ所
8は7ヶ所
 3は24か所
3は24か所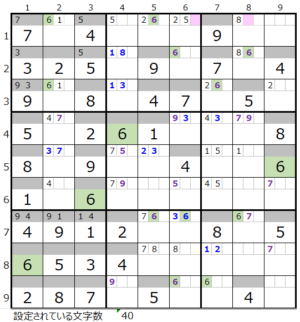 6は2か所
6は2か所 9は8ヶ所
9は8ヶ所
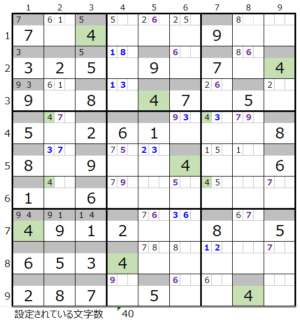 4はゼロ
4はゼロ 7は4ヶ所
7は4ヶ所
②難易度「低」の中に特異点が無いか?を確認する
この問題で難易度「低」に当たるのは、数字の「4」「5」「6」「7」の4つになります。
数字の「4」はスクウェアの形にメモ欄にセットされているので、これ以上は何もすることはできません。
数字の「5」と「7」は特異点は無さそうです。
※数字の連鎖(横方向、縦方向でメモ欄にある同じ数字を2つずつつなげて行く。なお一つのブロックに入る同じ数字も2つにする)に関してはは1つの場合と、スクウェアが存在する2つの場合がありそうですが実際に残るパターンは少なそうです。数字の連鎖の仕方については後段でご説明致します。
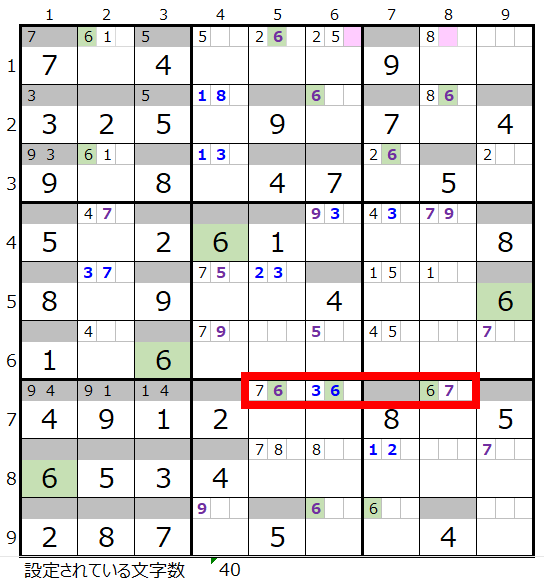
注目していただきたのは数字の「6」になります。
数字の「6」の7行目のメモ欄を見ていただきたのですが、左図赤枠には3つのマス目のメモ欄に数字の「6」が存在しています。
最初の「6」は縦方向での解法その2から
次の「6」は解法その3から
最後は解法その1から
3つそれぞれ別な解法からセットされたものになります。
ただ「色分け手法」を使用する場合、横方向、縦方向、ブロックでそれぞれ同じ数字が2つになる必要があります。
なお今回の問題での特異点は「2つを超える同じ数字が同じ行または列に並んでいる点」でしたが、特異点はこれだけではありません。
その他の特異点につきましては別の回でご紹介して行く予定です。
③特異点のある数字の「6」の場合の連鎖を考える
数字の連鎖のやり方は解法その4の場合と変わらないのですが、可能性のあるマス目を含めてすべてのパターンを見出す作業は確かに大変です。
ただし連鎖を考える際に必ず「通らなければならないマス目」と「横方向、縦方向でメモ欄にある同じ数字を2つずつつなげて行き一つのブロックに入る同じ数字も2つにする」というルールからチェーンの仕方が絞られてくる認識です。
- 必ず通らなければならないマス目は下記になります。
- 解法その1でセットされた(確認しようとしている)数字がメモ欄にある。
- 同一行または同一列に数字がセットされている場合はお互いに数字が結ばれる必要があります。
- 解法その2でセットされた(確認しようとしている)数字が横方向、縦方向の並びでメモ欄にある。
- これに該当する場合は連鎖する時にお互いの数字が結ばれる必要があります。
- 横方向または縦方向で残り2マスになっている(確認しようとしている)数字がメモ欄にある。
- これに該当する場合は連鎖する時にお互いの数字が結ばれる必要があります。
- 解法その1でセットされた(確認しようとしている)数字がメモ欄にある。
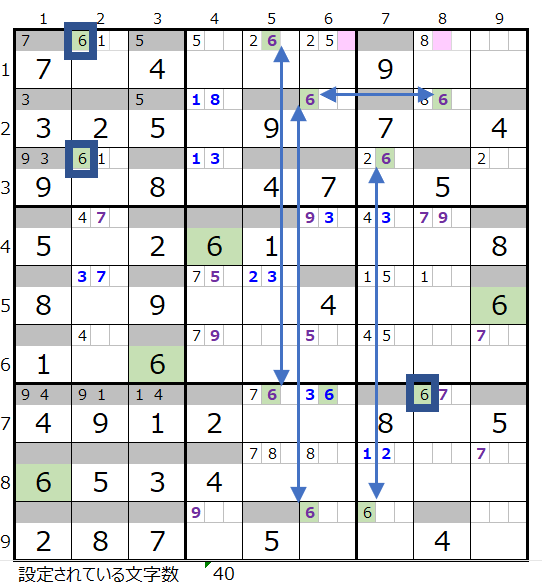
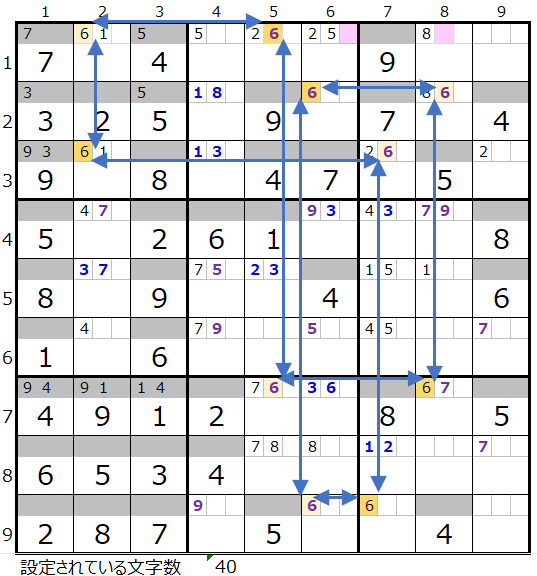
左図で紺の四角で括られた数字は上記「1」の説明に該当します。
また縦方向の矢印3つと横方向の矢印1つが結んでいる数字は上記「2」の説明に該当します。
ここまでつながりが示されているので、残りの矢印を引くのは難しくないと思います。
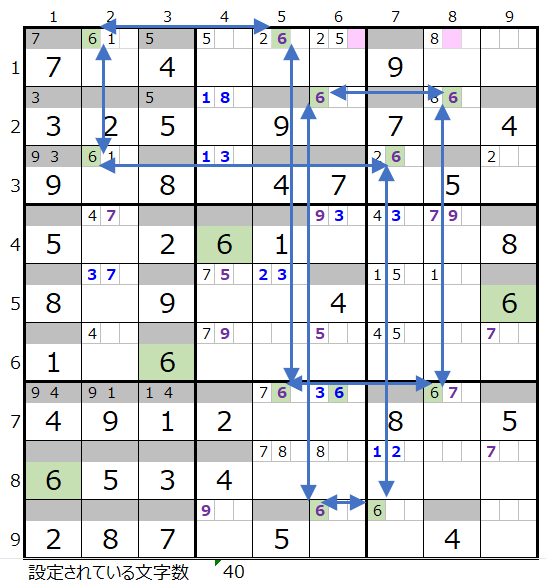
結び形としては左図の形しか考えられない認識です。
なお左図の連鎖はまだ「6」が決まっていない5つのブロックすべてを結ぶ形になります。
この場合は「6」が入る可能性のある箇所として背景色薄ピンクを付けたマス目は通らないことになります。
⑤連鎖の数字を色分けする
次に連鎖に沿って数字を色分けして行きます。
その結果が左図になりますが、この色分けは残念ながら成立しません。
なぜならば第1ブロックは「薄・濃」のペアとなりますが、それ以外の第2、第3、第8、第9ブロックは「濃・濃」、「薄・薄」の組み合わせとなっています。
色分けされたどちらかに数字の「6」をセットするのですが、1つのブロックに同じ濃さの色は存在してしまうと、1つのブロックに数字の「6」を2か所セットすることになり、それはできないので不成立になります。
※ただし一般的には、今回のように色分けが不成立になるのはレアケースとなります。
今回使用させていただいている2015年11月の問題集の中の「数独問題集(達人級)」全48問の内、「色分けの手法」を適用した中での感覚で恐縮ですが、色分けをして不成立になるのは1割以下である認識です。
なお色分けが成立した場合の手順につきましては別の回でご説明致します。
⑥色分けが成立しない場合の対処法
色分けが成立しない場合ですが、良くあるのは別の数字の連鎖が存在しているケースです。
ただし今回の問題は残念ながら上記の連鎖以外にはルールに従ってすべての数字をつなげることはできません。
そうなると次の対処法としては、連鎖するブロックを減らして別の連鎖が存在しないか?確認することになります。
現在5つのブロックが残っているので1ブロック減らして4ブロックで連鎖ができるか?考えた時に減らすのであれば出っ張っている第1ブロックを減らすのが良い認識です。
第2、第3、第8、第9ブロックの背景色薄ピンクを含めたマス目をつなぐ連鎖としては一筆書きでは存在しそうにありません。
となると次にスクウェアでの配置ができないか?を確認します。
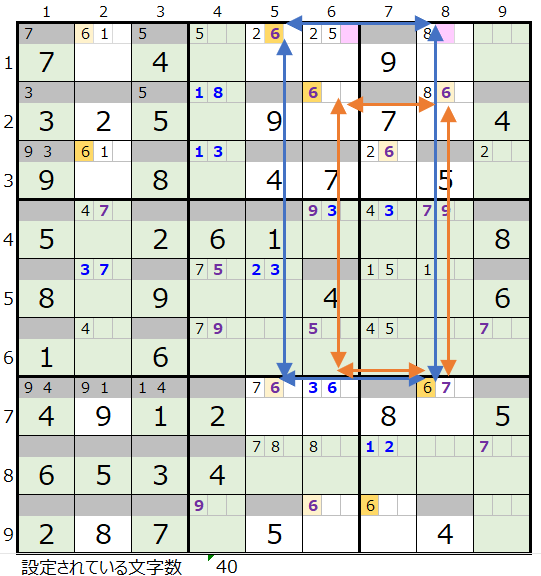
4つのブロックで考えると例えば左図のような紺とオレンジのようなスクウェアが考えらますが、残念ながら2つのスクウェアの4つの角のいづれかを共有しないと配置することができず、という事は4つのブロックでは連鎖が存在しない事になります。
角を共有するということは、横方向、縦方向で同じ数字が2つ存在することになってしまうからです。
そうなると更にブロックを減らすことになるのですが、3つのブロックでの連鎖は4つのブロックの時にも確認しましたが存在しそうにありません。
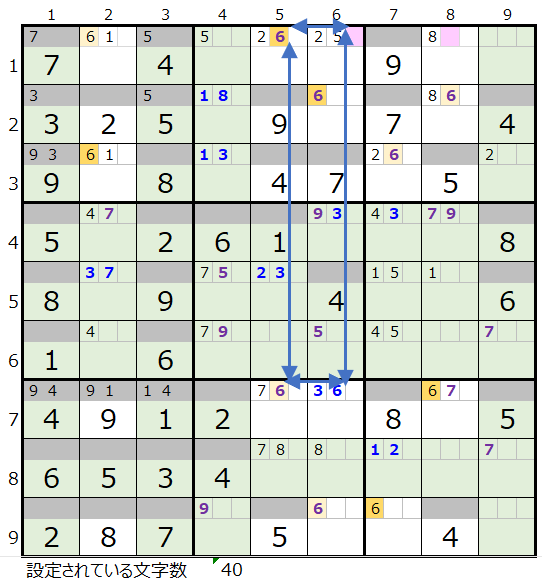
そうなりますと2つのブロックでのスクウェアとなり、最終的に左図の形に絞られる認識です。
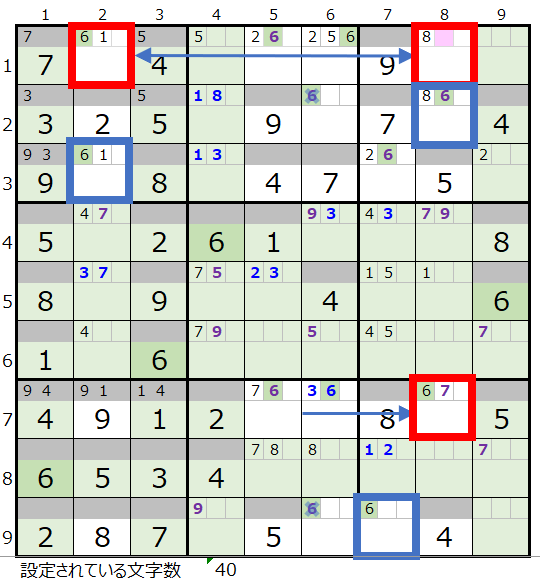
スクウェアの形でメモ欄に数字の「6」がセットされると、同じブロックの他のマス目には「6」は入らない事になります。
そうすると解法その1から第1と第9ブロックの赤枠には「6」が入らない事が確定するので、第1、第9ブロックは紺枠に「6」が入ります。そのため第3ブロックも紺枠に「6」が入ることになります。
まとめ
今回使用させていただいた問題は前回第9回で二択分岐の使用例としてご説明したものでしたが、今回はそれを色分け手法を用いた場合の解き方についてご説明いたしました。
従いまして「色分け手法」をご説明するために例題としては少し特殊な形になっている認識です。
また最終的な連鎖が2ブロックでのスクウェアとなるために「色分の正誤を判断するための手法」につきましては出番がありませんでした。
ところで「色分け手法」として「5ブロックから2ブロックに連鎖を減少させるところの展開は汎用性があるものなのか?」と言われると、今回の問題の数字の配置の妙によるところが大きいというのが正直なところです。
ただし連鎖に不整合がある場合「他の選択肢がない時は連鎖の縮小を考える」というのは経験上のセオリーとなります。
なお色分け手法は解法その1からその3のように「明確に作業内容が決められている」わけではなく、連鎖を見つけ出すところが「解法その2の結びつきや配置の状況を判断しながら数字が入るマス目を見つけ出す」しかないのなので、連鎖を見つけ出す経験値が必要であったり、またある程度の試行錯誤が起こりえる認識です。
そのためまずは難易度「低」の中で易しそうに見えるものを選んで試して見ていただければ幸いです。
この後も、2015年11月の問題集の中の「数独問題集(達人級)」の問題をお借りしていつくかの事例をご紹介されていただきたく存じます。
以上、最後までお読みいただき誠にありがとうございました。

