これまで14回に渡り「解法その1」～「解法その4」そして「色分けの手法」をご説明して来ましたが、前回の第15回から数回に渡り最終回として、第1回の時にご紹介した「世界一難しい数独」の問題に「色分けの手法」を使って再度ご説明して行きます。
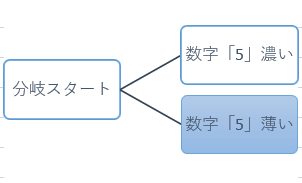
前回は最初の盤面から数字「5」を複数連鎖の共通して通過するマス目から「濃い」「薄い」2か所づつ仮置きした二択分岐ところまでをご説明しましたが、今回は「薄い」場合のその後の展開となります。
今回の説明で使用する数独問題について
第1回の時にもご紹介していますが、今回の問題は2012/7/3日付の「ロケットニュース24」に掲載されている「世界一難しい数独」になります。
一回目二択分岐その1「薄い」「5」で仮置きをした盤面
この盤面は第15回「世界一難しい数独その1」からの続きになりますが、文字数は23文字で本解法その1から3では盤面として行き詰まった状態です。
左図のメモ欄
・黒字茶字—解法その1からセット
・太青—解法その3からセット
メモ欄で該当する数字が置ける場所を確認する
前回「世界一難しい数独その1」でも1から9のすべての状況は確認しているのでが、2か所仮置きした事でどのくらい差が生じるのか?確認したく、再度調べて見ます。
背景色薄ピンク色のところは該当する数字が置ける場所になります。
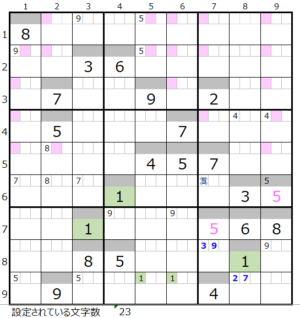数字「1」–前回20ヶ所→今回同数
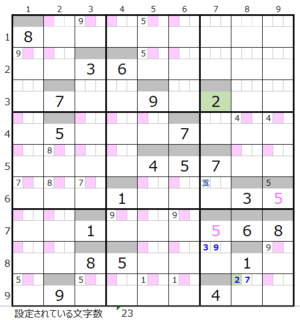
数字「2」–前回44ヶ所→今回42ヶ所
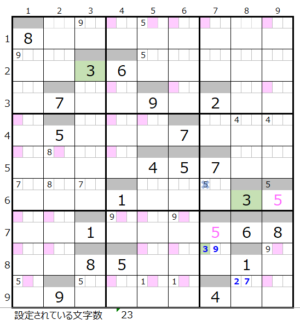
数字「3」–前回30ヶ所→今回29ヶ所
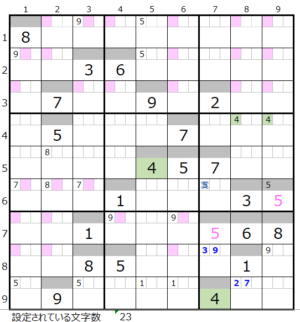
数字「4」–前回32ヶ所→今回27ヶ所
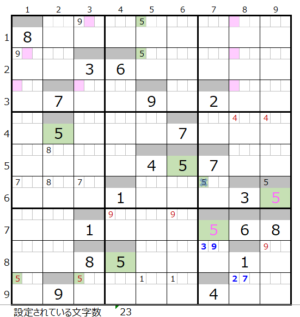
数字「5」–前回18ヶ所→今回7ヶ所
数字「6」–前回31ヶ所→今回30ヶ所
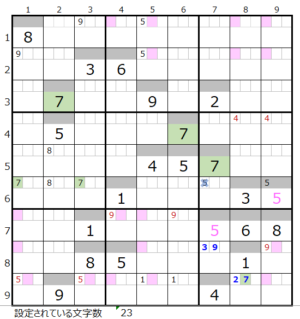数字「7」–前回19ヶ所→今回18ヶ所
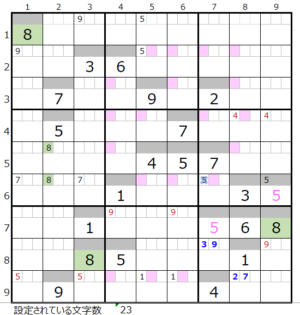
数字「8」–前回19ヶ所→今回同数
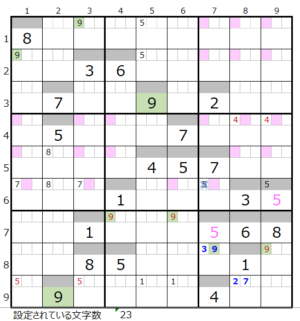
数字「9」–前回26ヶ所→今回21ヶ所
薄ピンク色の数が少ない数字の複数連鎖を考える
前回と比べて大きく減ったのは、仮置きした「5」を除くと数字「4」と「9」になります。ただそうは言ってもまだかなりな数が残っているのでこれらの数字を候補にするのは難しいところです。
結果を見渡すと薄ピンク色の数が少ないのは数字「5」の7ヶ所、「7」の18か所、「8」の19ヶ所、になりますが実際に試して見ると残念ながら数字「7」と「8」ともに複数連鎖の対処法では効果のある数字は存在していませんでした。
効果があるとは「濃い」「薄い」でそれぞれ2つ以上共通して通過するマス目が存在する事を意味しています。
という事で、今回も数字「5」を再度考える事にします。
数字「5」で再度連鎖を考える
成立する連鎖はつぎの2つになります。
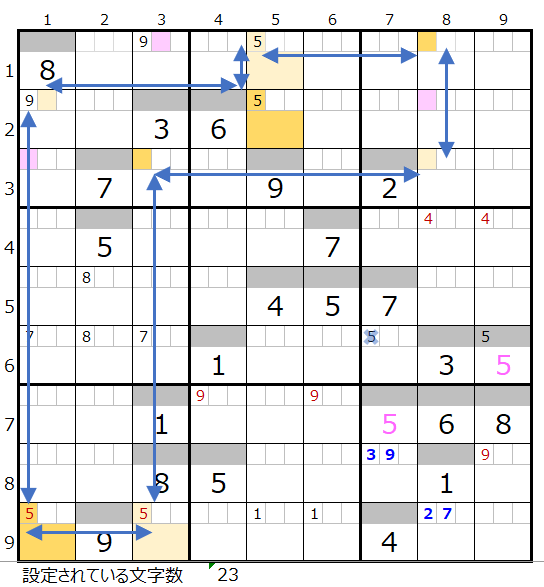
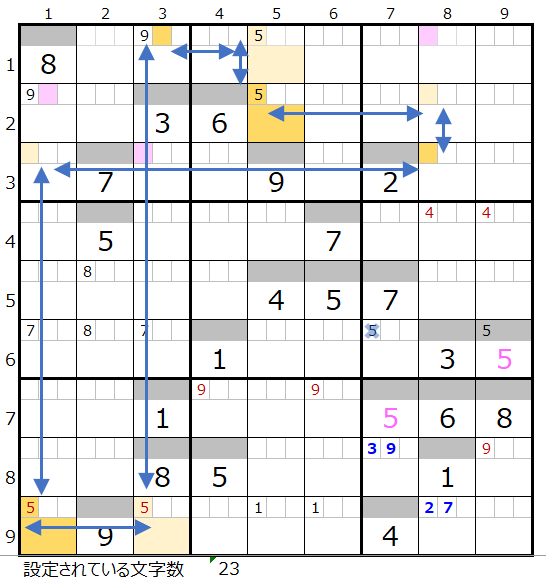
共通して通過するマス目は「濃い」「薄い」背景色を付けた2か所づつになります。
この中にはスクウェアになり得る箇所は含まれていないので、それぞれの箇所に「5」をセットして二択分岐で解き進めます。
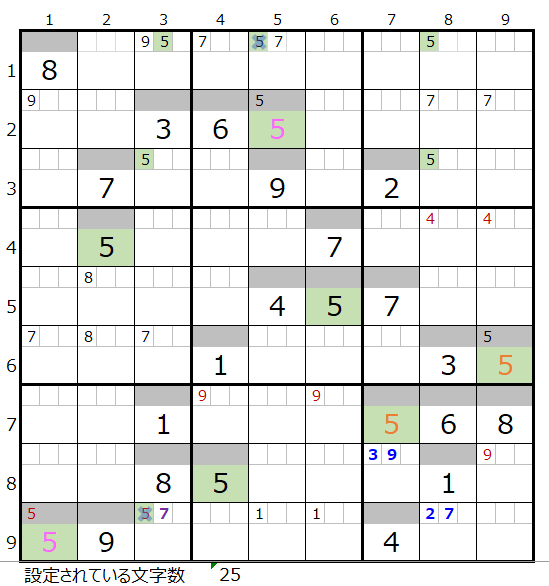
「濃い」方はメモ欄に情報が追加されるだけで数字の解決はありません。
その先をこの後の章で確認して行きます。
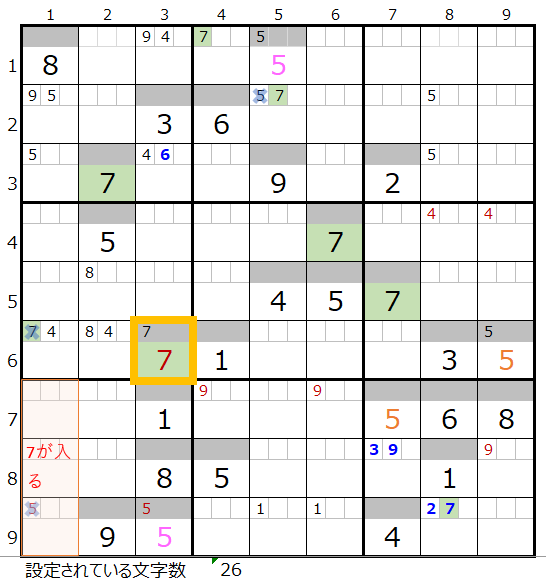
「薄い」方は黄枠「7」が決まりますが、盤面としては行き詰まった状態です。
こちらの分岐は次回ご説明をいたします。。
二回目の二択分岐その1「薄い」「5」での盤面
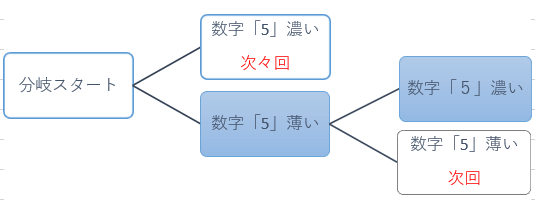
この章でご説明するのは左図2つ目の数字「5」濃いの場合です。
数字「5」薄いにつきましては次回ご説明致します。
メモ欄で該当する数字が置ける場所を確認する
背景色薄ピンク色の数字が置ける場所の数で大きく変化したのは下記になります。
- 数字「5」は「7ヶ所」→「0ヶ所」
- 数字「7」は「18ヶ所」→「9か所」
「0ヶ所」の場合、その数字で二択分岐することは可能ですが、同じ数字だけ解決して全体を解き進める事はできないので今回は数字「7」を選択します。
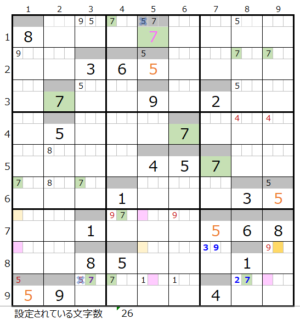
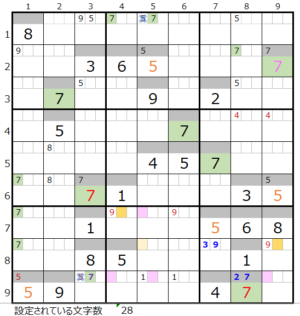
数字「7」で連鎖を考える
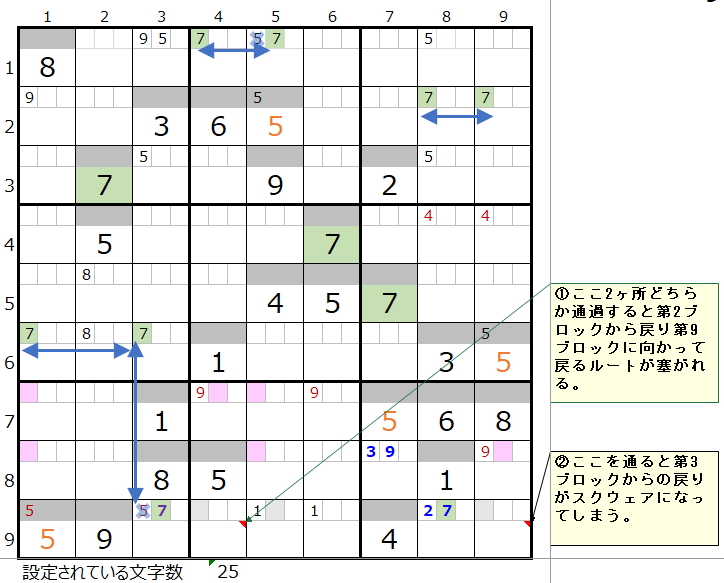
9行目の背景色灰色のところは、左図コメントに記載している理由により通過するマス目にすることができません。
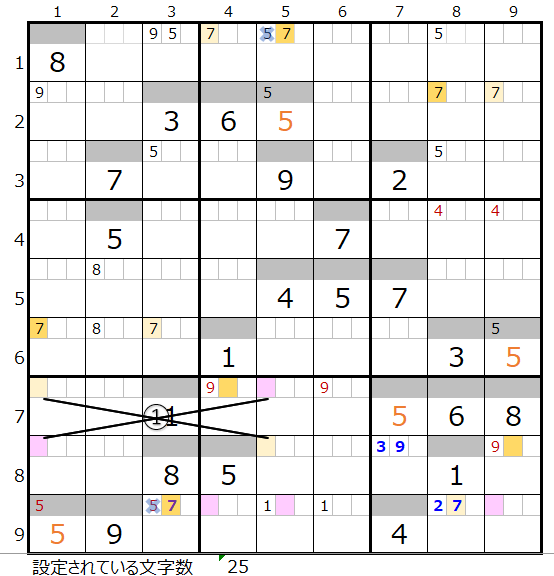
上左図のような色分けの正しい連鎖が見つかります。
ただし①の箇所が対角での置き換え可能です。
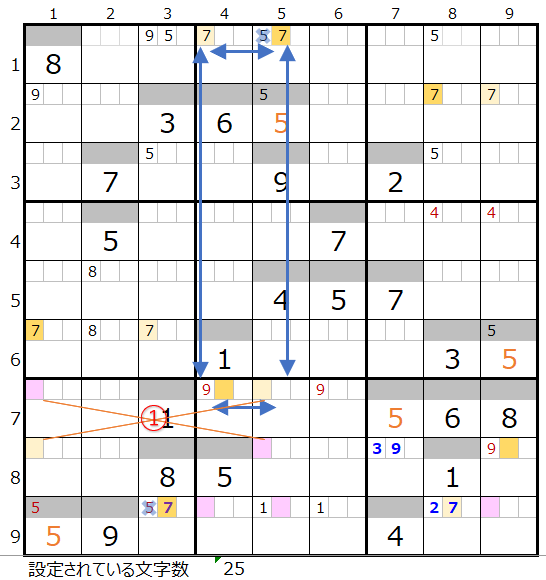
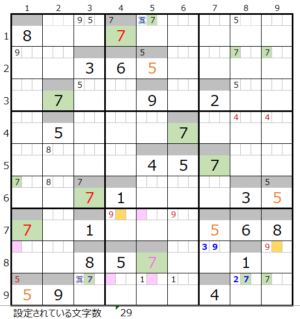
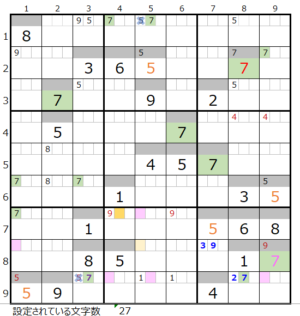
実際に確認して見ると、上右図のようにスクウェアができるので成立しない事が解ります。
そうなると連鎖が一つとなり「色分けの手法」を使用することができます。
残りのブロックが5つなので、「仮置きしたマス目以外は解けない」個数は有効です。
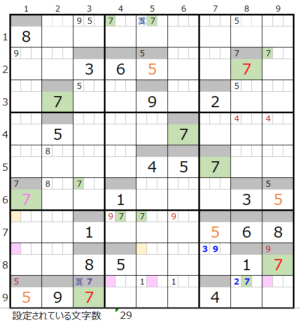
①第4ブロック→第7ブロック→第9ブロック→第3ブロック
カウントは「濃い」2/3
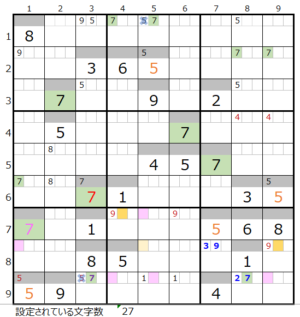
②第7ブロック→第4ブロック
カウントは無し
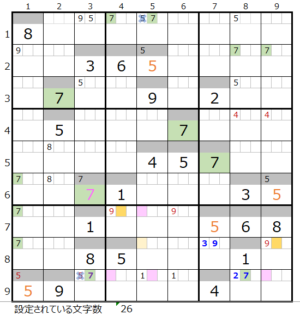
③第4ブロック
カウントは無し(薄い)
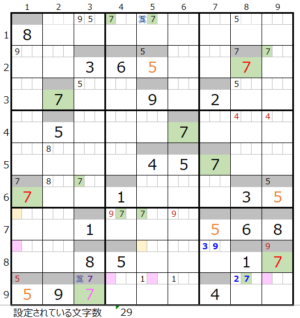
④第7ブロック→第4ブロック→第9ブロック→第3ブロック
カウントは「濃い」2/3
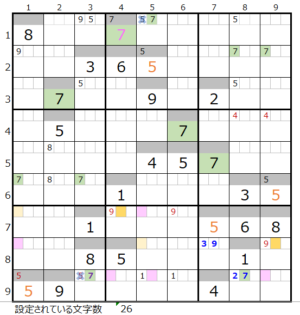
⑤第2ブロック
カウントは無し(薄い)
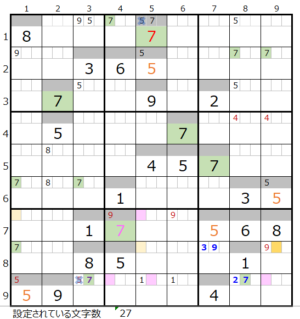
⑥第8ブロック→第2ブロック
カウントは無し
⑦第2ブロック
カウントは無し(濃い)
⑧第8ブロック→第7ブロック→第4ブロック→第2ブロック
カウントは「薄い」2/3
⑨第3ブロック
カウントは無し(濃い)
⑩第9ブロック→第4ブロック→第3ブロック
カウントは「薄い」1/2
⑪第3ブロック→第9ブロック→第4ブロック
カウントは「薄い」1/2
⑫第9ブロック→第3ブロック
カウントは無し
以上により、カウントの結果としては
・濃い—2/3,2/3
・薄い—2/3,1/2,1/2
となり、「薄い」が「1/3」だけ大きいのですが半分以上の差が無いため明確な差になりません。
また「 仮置きしたマス目以外は解けない 」個数は
・濃い—2ヶ所
・薄い—2ヶ所
の同数となり、この結果から「濃い」2/3、「薄い」1/2で二択分岐することになります。
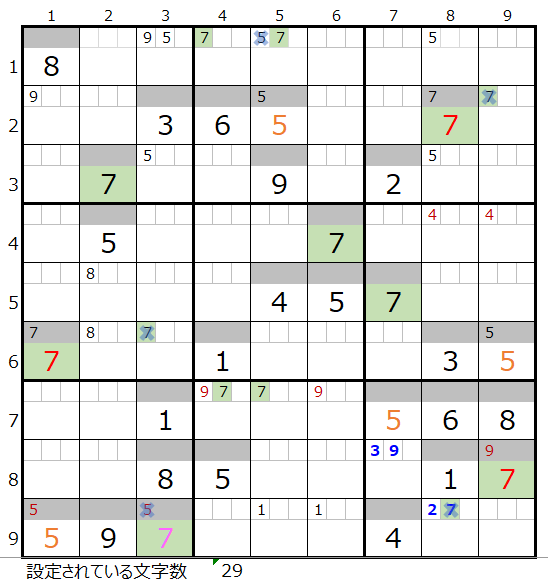
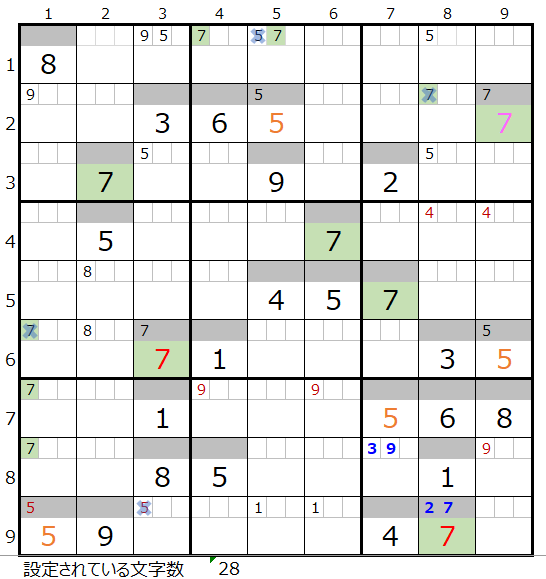
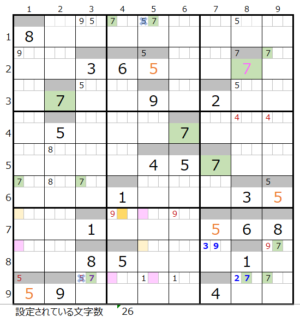
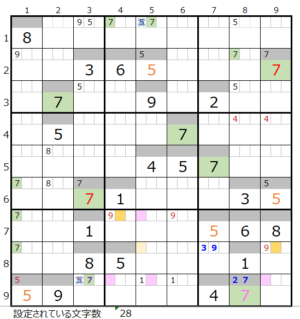
両者を解き進めるとそれぞれ下記盤面になりますが、両者ともに盤面としては行き詰まった状態です。
・背景色の付いているマス目が解決したところです。
・なおメモ欄につきましては背景色は省略しています。
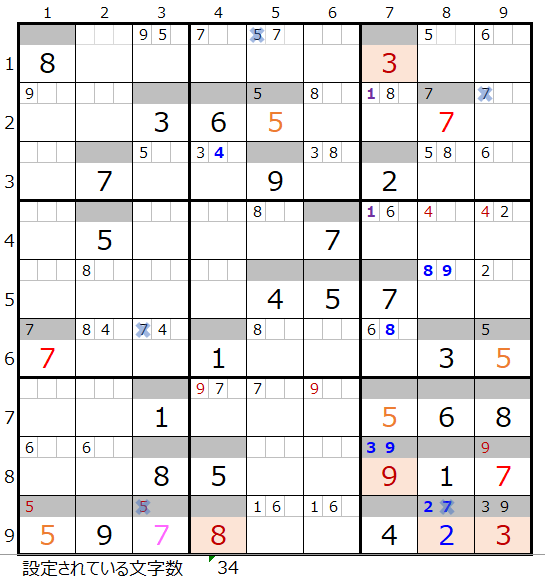
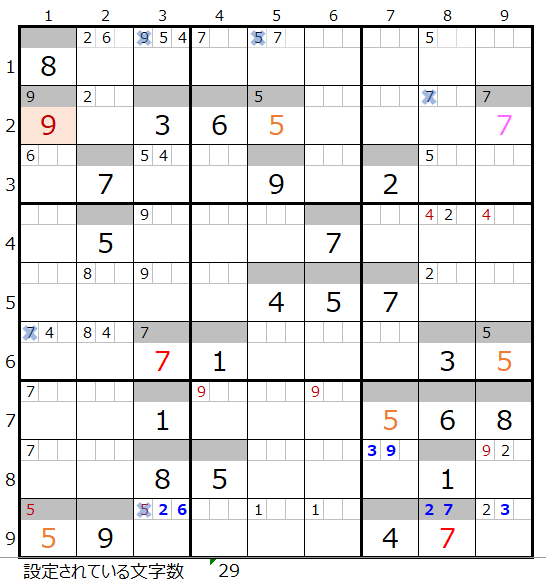
この後の章で、まず「濃い」場合のその先を確認し、さらに後段で「薄い」場合を確認して行きます。
三回目の二択分岐その1「濃い」「7」での盤面
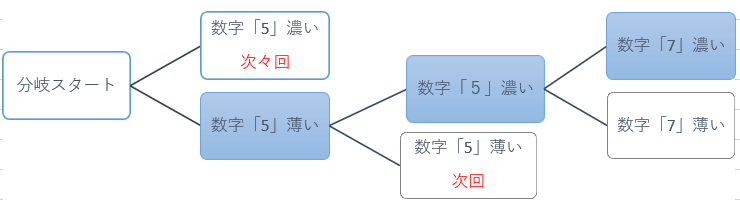
この章でご説明するのは左図数字「7」濃いの場合です。
数字「7」薄いにつきましては後段でご説明致します。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 16 | 29 | 15 | 22 | 0 | 14 | 0 | 2 | 14 |
数字「8」が2か所になるので「8」を選択します。
数字「8」で連鎖を考える
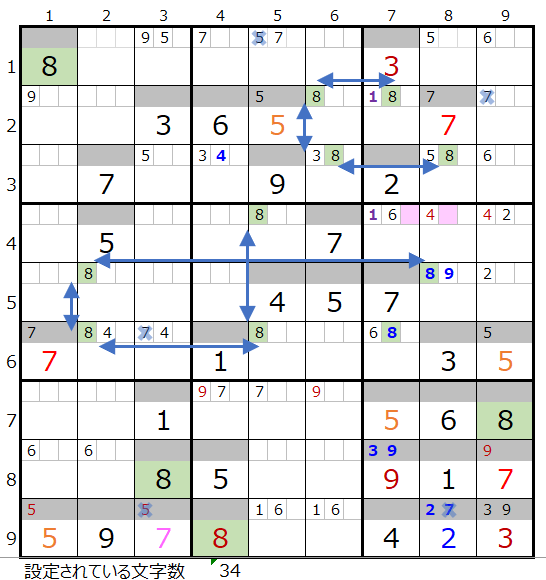
メモ欄にセットされた数字で紐づけできるところを結ぶと上左図のようになり、おのずと連鎖は見つかることと存じます。
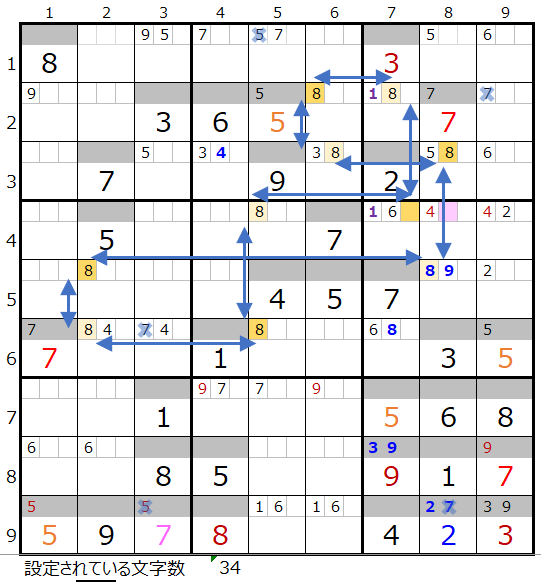
色分も正しい事が解ります。
対角での置き換え可能なポイントもありません。
連鎖が一つとなり「色分けの手法」を使用することができます。
残りのブロックが5つなので、「仮置きしたマス目以外は解けない」個数は有効です。
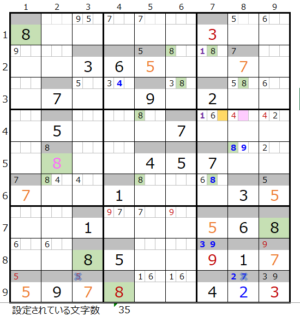
①第4ブロック
カウントは無し(濃い)
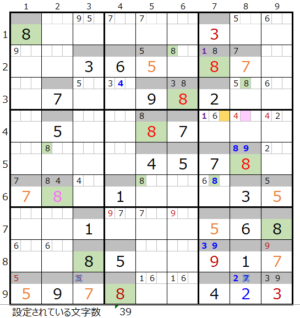
②第4ブロック→第5ブロック→第6ブロック→第2ブロック
カウントは「薄い」1
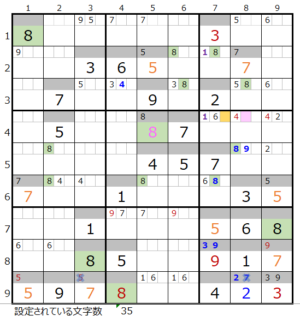
③第5ブロック
カウントは無し(薄い)
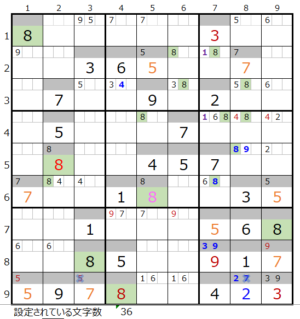
④第5ブロック→第4ブロック
カウントは無し
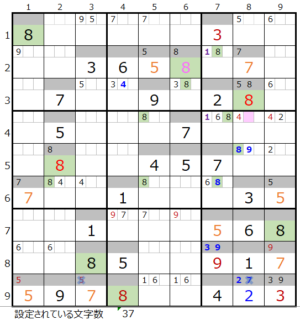
⑤第2ブロック→第3ブロック→第4ブロック
カウントは「濃い」3/5
⑥第2ブロック→第3ブロック
カウントは無し
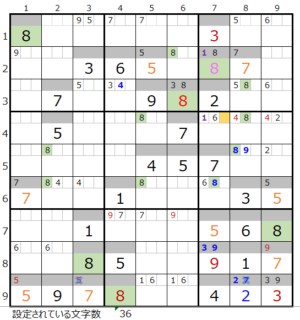
⑦第3ブロック→第2ブロック
カウントは無し
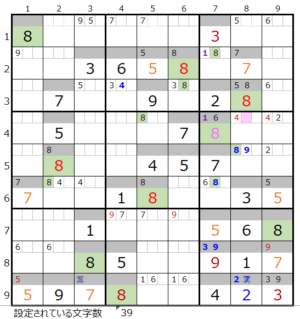
⑧第6ブロック→第5ブロック→第4ブロック→第3ブロック→第2ブロック
カウントは「濃い」1
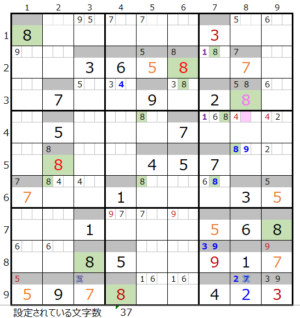
⑨第3ブロック→第4ブロック→第2ブロック
カウントは「濃い」3/5
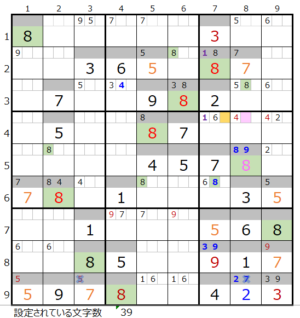
⑩第6ブロック→第5ブロック→第4ブロック→第3ブロック→第2ブロック
カウントは「薄い」1
以上により、カウントの結果としては
・濃い—1,3/5,3/5
・薄い—1,1
となり、「濃い」が「1/5」だけ大きいのですが半分以上の差が無いため明確な差になりません。
また「 仮置きしたマス目以外は解けない 」個数は
・濃い—1ヶ所
・薄い—1ヶ所
の同数となり、この結果から「濃い」3/5、「薄い」1で二択分岐することになります。
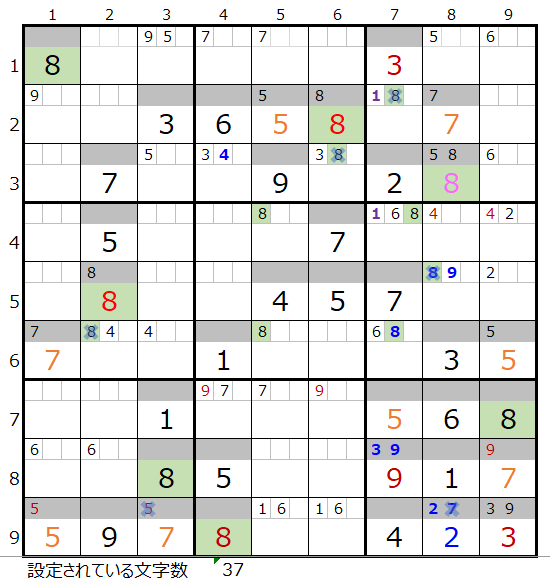
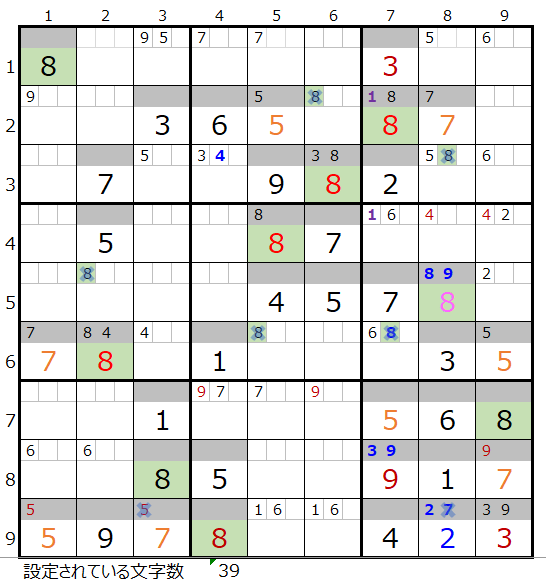
両者を解き進めるとそれぞれ下記盤面になります。
残念ながら両者ともに途中で手詰まり(解けない)という結果になります。
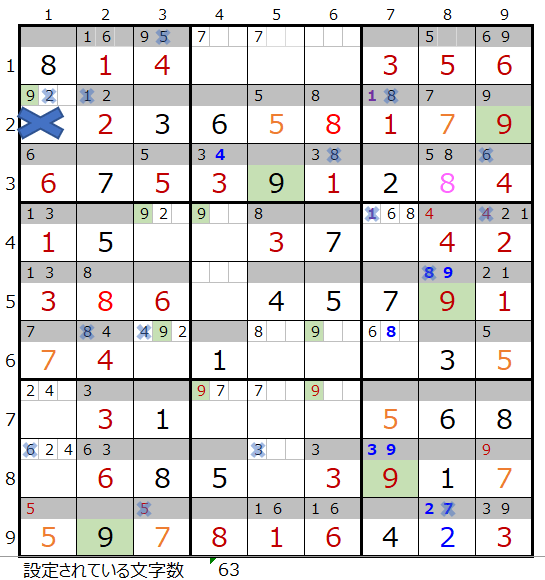
第1ブロックに数字「9」が入らない事が解ります。
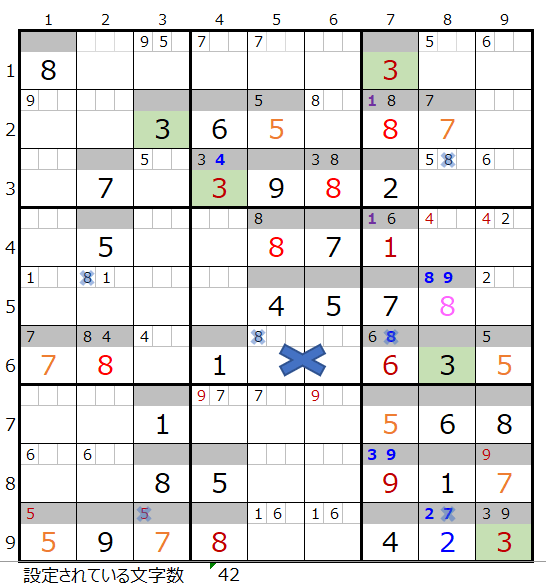
第5ブロックに数字「3」が入らない事が解ります。
以上の結果から、『三回目の二択分岐その1「濃い」「7」』の分岐には正解が無い事が解りました。
続けて、もう片方の『三回目の二択分岐その1「薄い」「7」』を調べて行きます。
三回目の二択分岐その2「薄い」「7」での盤面
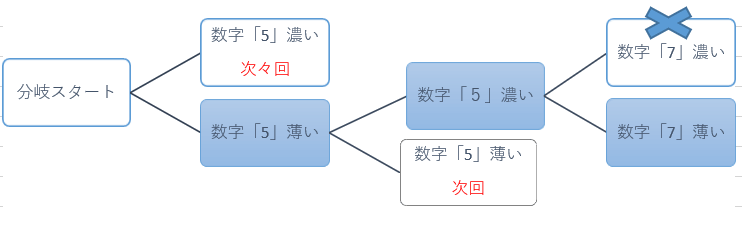
『数字「7」濃い』には正解が無い事が解りましたので、三回目の二択分岐その2として『数字「7」薄い』を見て行きます。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 17 | 28 | 27 | 17 | 0 | 24 | 3 | 18 | 12 |
数字「7」は残り3ヶ所なので後回しとすると、数字「9」が12か所になるので「9」を選択します。
数字「9」で連鎖を考える
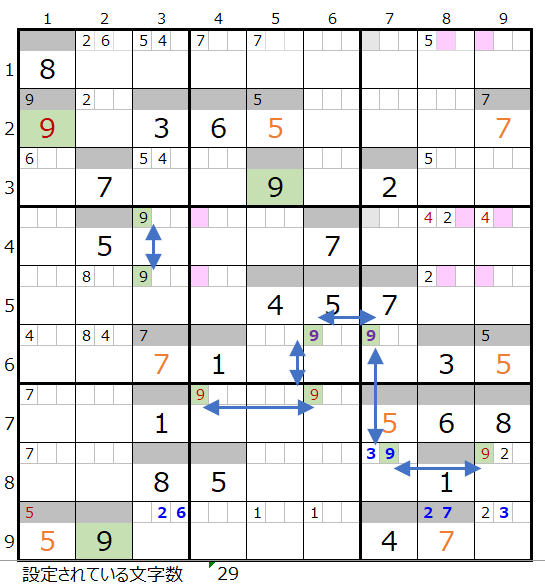
メモ欄にセットされた数字で紐づけできるところを結ぶと上左図のようになります。
7列目の背景色灰色のところは既にその列で2か所置き場所が決まっているためにそれ以上置くことができないことを表しています。
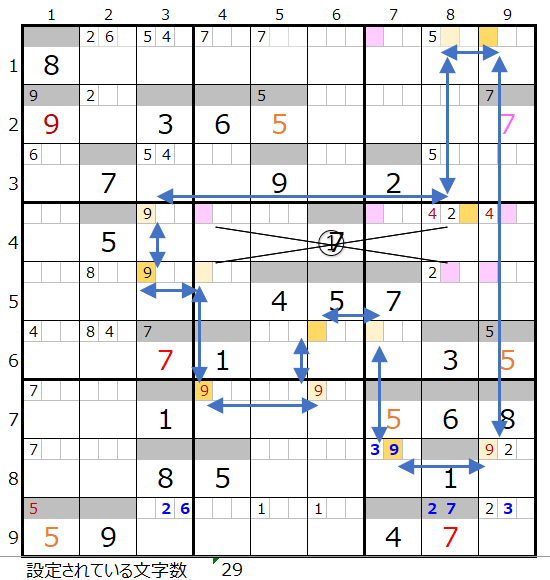
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換え可能なポイントは1ヶ所(①)になります。
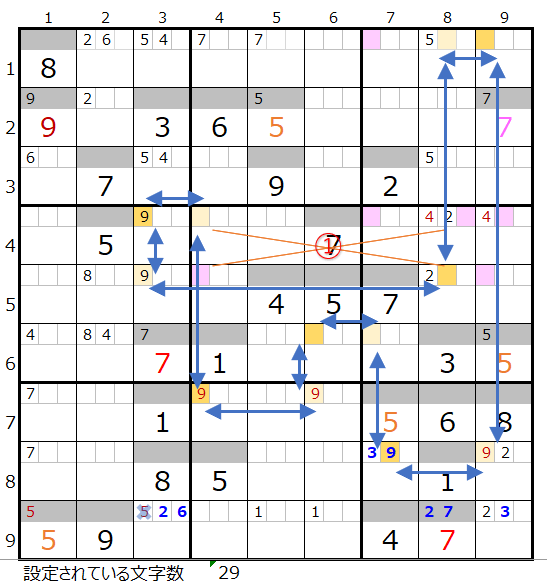
①を置き換えて見ると、上左図のようにもう一つの連鎖が成立することが解ります。
またこれ以上の残り全てのブロックを通過する連鎖は存在しない認識です。
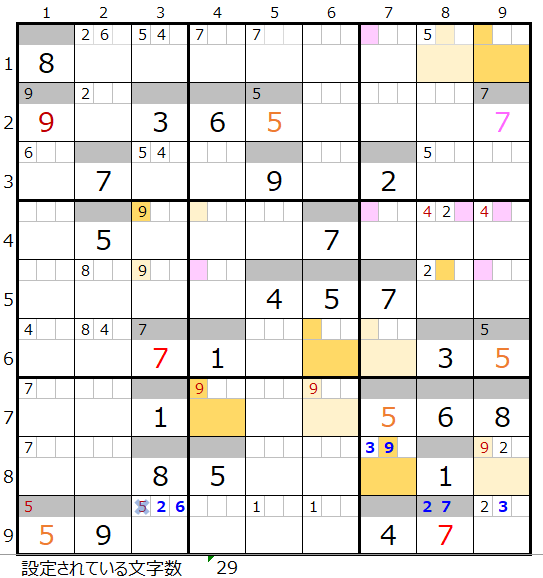
2つの連鎖で共通して通過するマス目に「濃い」「薄い」で背景色を付けると上右図のようになります。
この情報をもとに「濃い」「薄い」での二択分岐をして行きます。
四回目の二択分岐「9」で「濃い」「薄い」
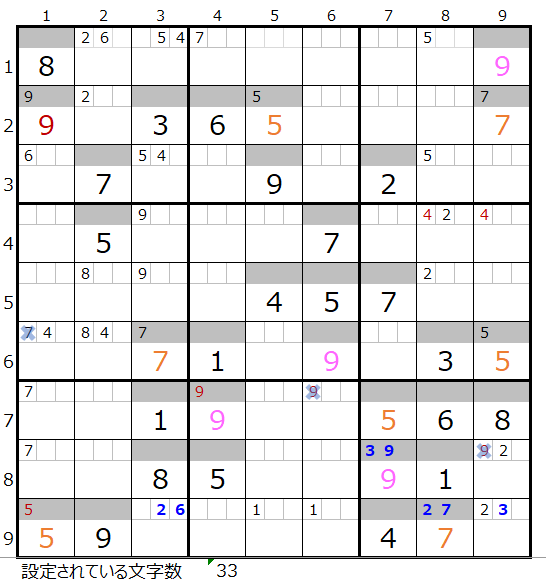
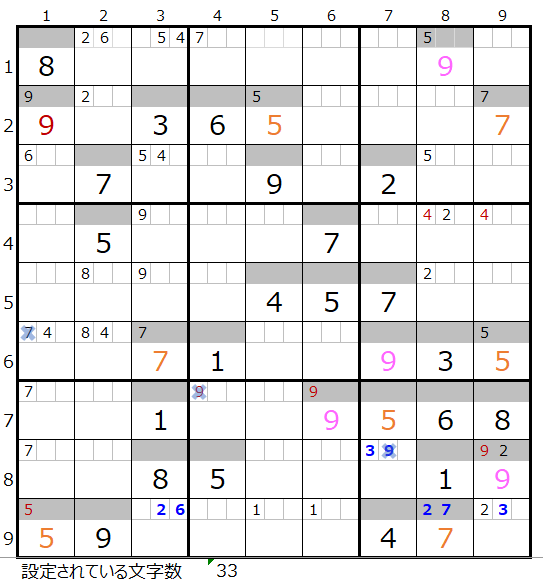
両者を解き進めるとそれぞれ下記盤面になります。
残念ながら両者ともに途中で手詰まり(解けない)という結果になります。
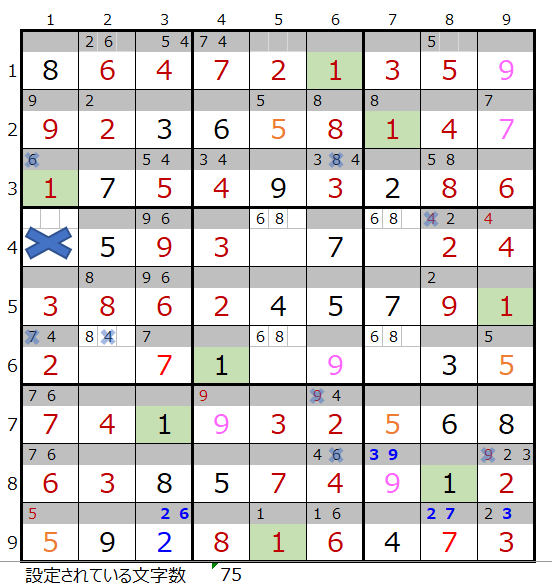
第4ブロックに数字「1」が入らない事が解ります。。
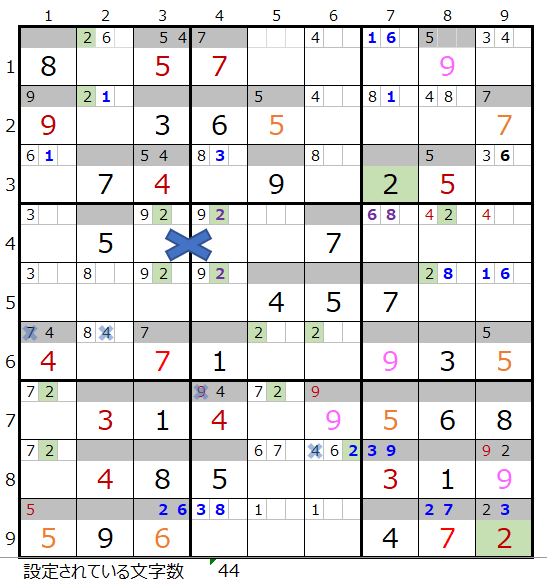
第4ブロックと第6ブロックの数字「2」のメモ欄の情報からは第5ブロックの「2」は6行目に入るはずなのに、4列目で「2」の入る場所が×印のマス目となり、これ以上解くことができません。
以上の結果から、『三回目の二択分岐その1「薄い」「7」』の分岐にも正解が無い事が解りました。
そうなりますと、今回確認した『二回目の二択分岐その1「薄い」「5」』の分岐には正解が無い事になります。
まとめ
今回は数字「5」での二回目の二択分岐で「濃い」場合のルートの最後までをご説明致しました。
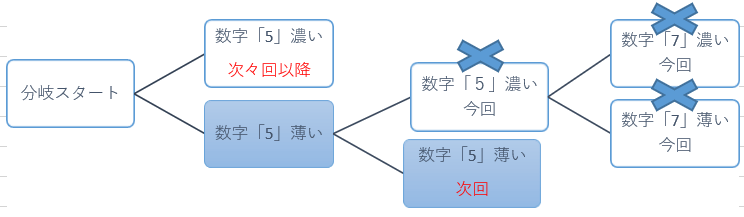
数字「8」まで
数字「9」まで
残念ながら、今回確認した『二回目の二択分岐その1「薄い」「5」』の分岐にし正解がありませんでした。
次回は数字「5」の二回目の二択分岐で「薄い」のその先についてご説明したく存じます。
最後までご一読いただき誠にありがとうございました。
