これまで14回に渡り「解法その1」～「解法その4」そして「色分けの手法」をご説明して来ましたが、今回の第15回から数回を最終回として、第1回の時にご紹介した「世界一難しい数独」の問題に「色分けの手法」を使って再度挑戦したいと思います。
今回も前回と同様にすべてのパターンを調べる事にしますのでボリューム的には大きくなりますので何回かに分けてご紹介したく存じます。
今回の説明で使用する数独問題について
第1回の時にもご紹介していますが、今回の問題は2012/7/3日付の「ロケットニュース24」に掲載されている「世界一難しい数独」になります。
なおこれまでと同様に途中から使用させていただいておりますが、配置されている数字はそのままで一か所も解けていません。
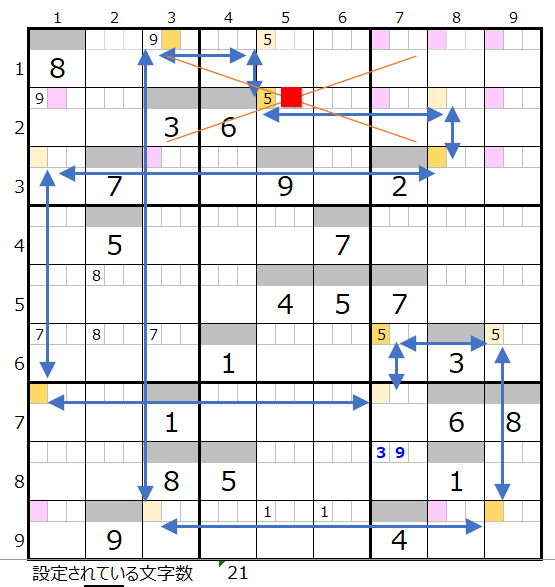
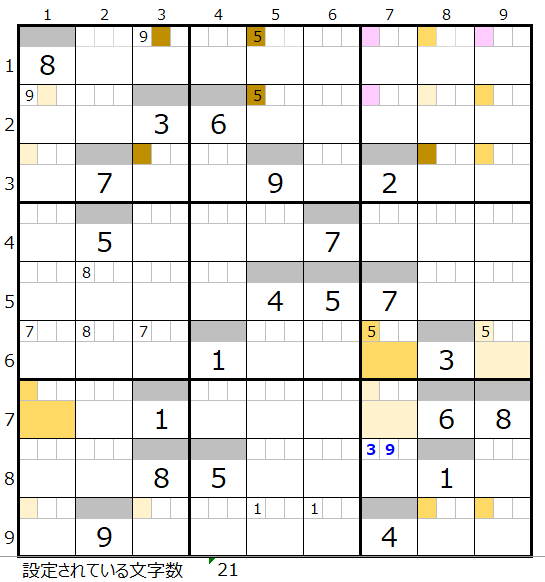
「解法その3」終了時の盤面(初期盤面のまま)
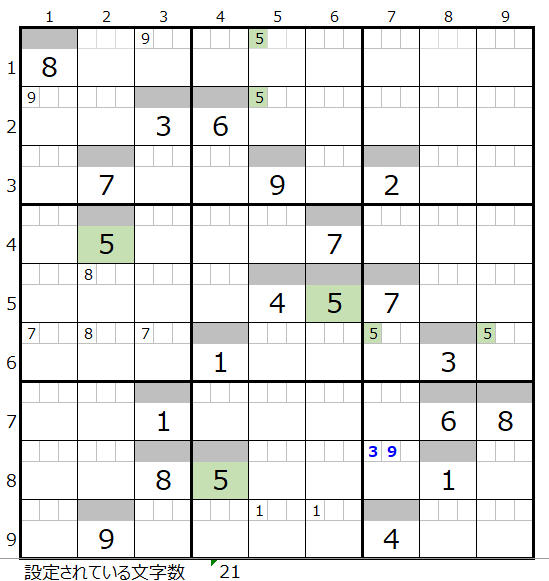
初期盤面のまま文字数は21文字です。本解法その1から3では盤面として行き詰まった状態です。
左図のメモ欄
・黒字—解法その1からセット
・太青—解法その3からセット
当然のことながらメモ欄には二択分岐以外での特異点はありません。
前回は二択分岐できる8行7列からスタートしましたが、今回は違う形で解き進めて行きたいと思います。
メモ欄にセットされている数字の状況を1～9すべて確認する
第9回でご説明した「色分け手法」の手順に従い、ブロックに入る可能性のある箇所のメモ欄の背景色を薄ピンクにセットして行きます。
なお説明のために可能性のある箇所の個数を数えていますが、ざっくりと難易度だけ把握すれば大丈夫です。
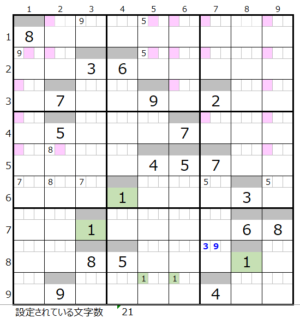数字「1」–20ヶ所
数字「2」–44ヶ所
数字「3」–30ヶ所
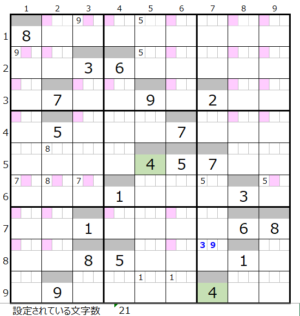
数字「4」–32ヶ所
数字「5」–18ヶ所
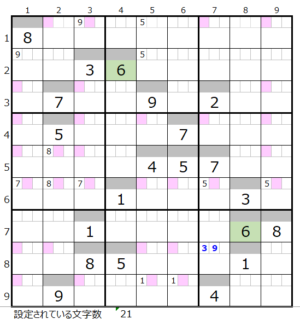
数字「6」–31ヶ所
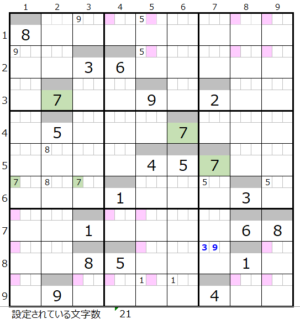数字「7」–19ヶ所
数字「8」–19ヶ所
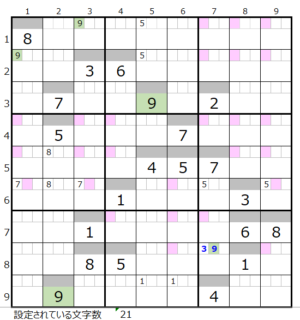
数字「9」–26ヶ所
難易度が相対的に低い数字の複数連鎖を考える
ほぼほぼ薄ピンク色の数ばかりなので圧倒されてしまいますが心掛けて折れないように頑張って行きたいと思います。
「色分けの手法」においては難易度の低い数字で連鎖を考えてユニークな連鎖を探し出すのが基本的なスタイルですが、この状況では「どの数字で連鎖を特定できるか?」が課題になります。
まずは薄ピンク色の数が「18」で一番少ない数字の「5」から考えて行きます。
なおそれ以外で候補を挙げるとすると「7–19ヶ所」「8–19ヶ所」「1–20ヶ所」になりますが、これだけ薄ピンク色の数が多いとすべてが複数連鎖が存在する形になりますので、「もっと効率の良い数字が無いか?」と探し回るよりも一つ数字を決めて取り組む方が良い認識です。
①数字「5」で連鎖を考える
その1
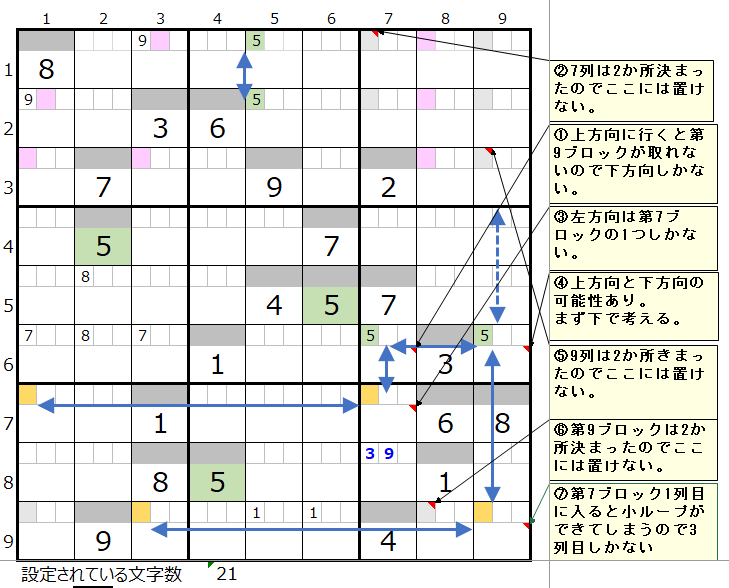
数字「5」は残り6ブロックですが、第2、第6ブロックは2ヶ所確定です。
第6ブロックからスタートしてどのようなルートがあるか面倒ではありますが網羅的に調べて行きます。
左図コメントを①から⑦まで順番に辿って行きます。
④では場合分けが存在しますが、それ以外は一意に決まって行くところを示しています。
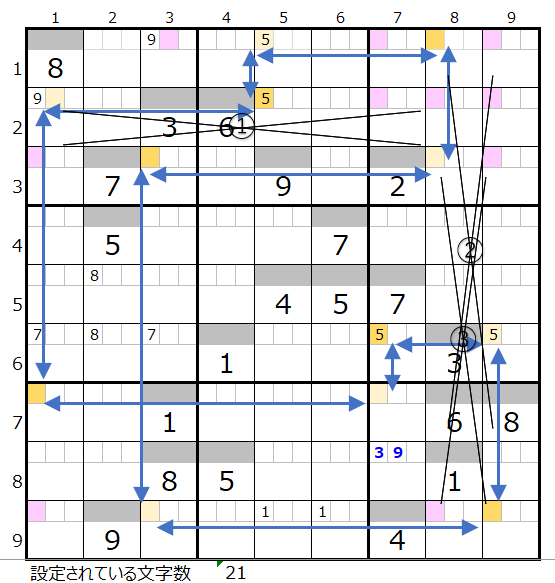
連鎖としては上左図のルートが色分けも正しいので一つ考えられますが、黒×印の①から③が対角線での置き換えが可能なポイントです。
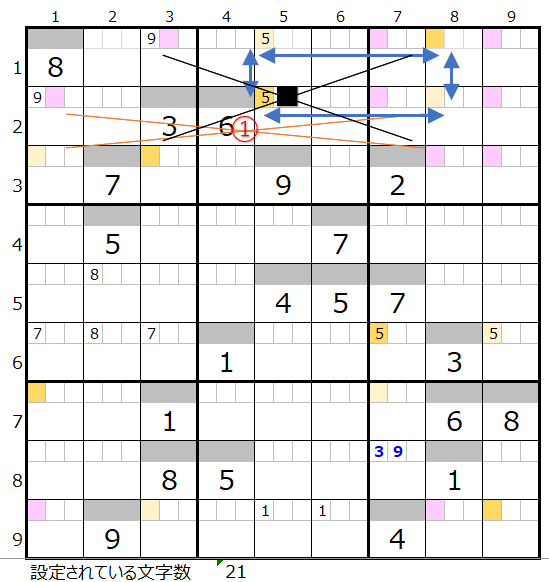
①の対角は上右図のようになり、スクウェアができるため対象外となります。
なお新たに■の対角が現れるので確認します。
左図は色分けが正しいもう一つの連鎖となります。
なお②と③につきまして、形が「その3」に該当しますので、後段「その3」の中でご説明致します。
その2
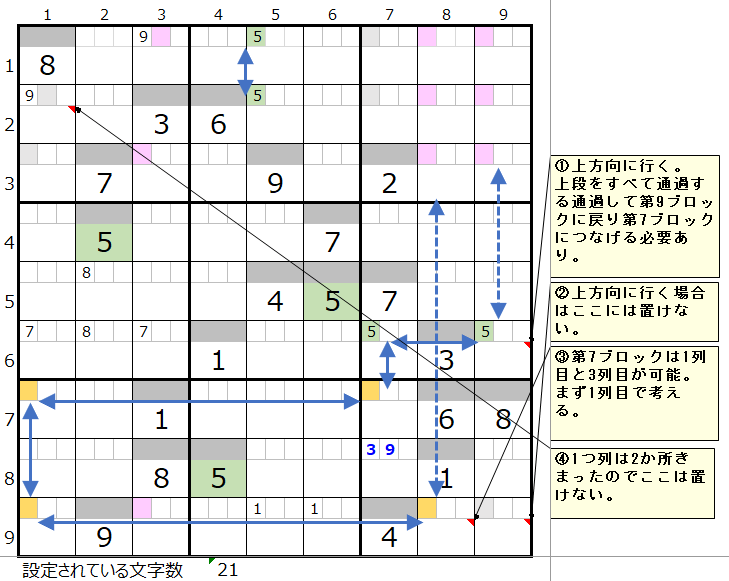
「その1」は第6ブロックの9傑目で下方向のルートを調べましたが、「その2」では上方向を調べて行きます。
左図コメントを①から④まで順番に辿って行きます。
③では9行1列と9行3列での場合分けが存在しますが、それ以外は一意に決まって行くところを示しています。
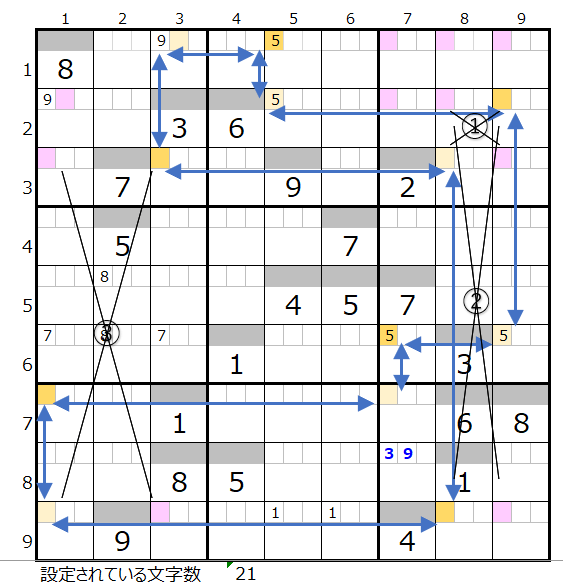
連鎖としては上左図のルートが色分けも正しいので一つ考えられますが、黒×印の①から③が対角線での置き換えが可能なポイントです。
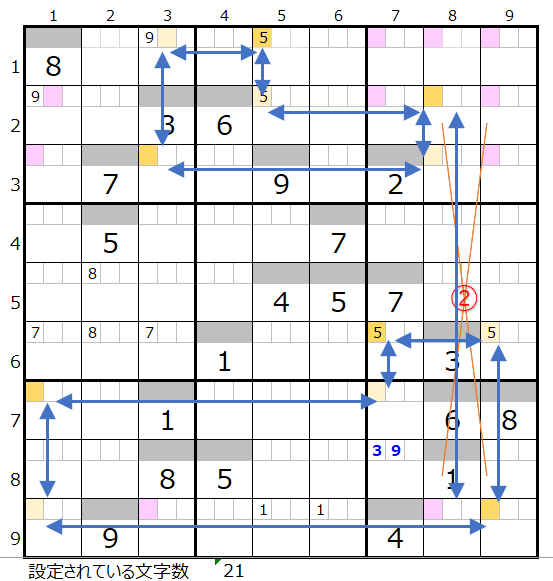
①の対角は上右図のようにもう一つの色分けが正しい連鎖があることが解ります。
②の対角は左図のように2つのループができるため対象外となります。
なお③につきまして、形が「その3」に該当しますので、後段「その3」の中でご説明致します。
その3
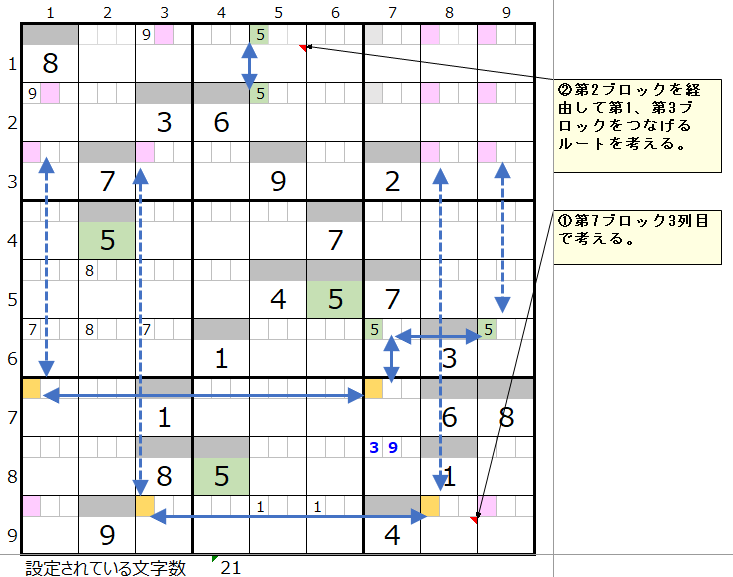
「その2」では第7ブロックの9行1列を通過するルートを調べましたが、「その3」では9行3列を調べます。
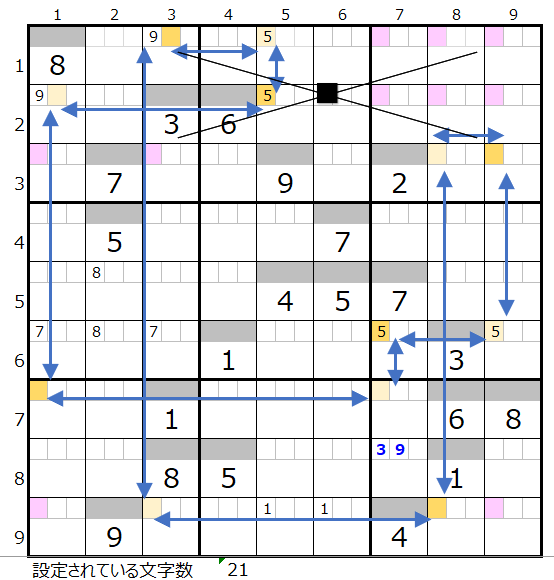
連鎖としては上左図のルートが色分けも正しいので一つ考えられますが、黒×印■のところが対角線での置き換えが可能な形です。
上左図赤枠の4ヶ所が「濃いと濃い」「薄いと薄い」の組み合わせになっているので、色分けが正しくありませんので、この連鎖は不成立となります。
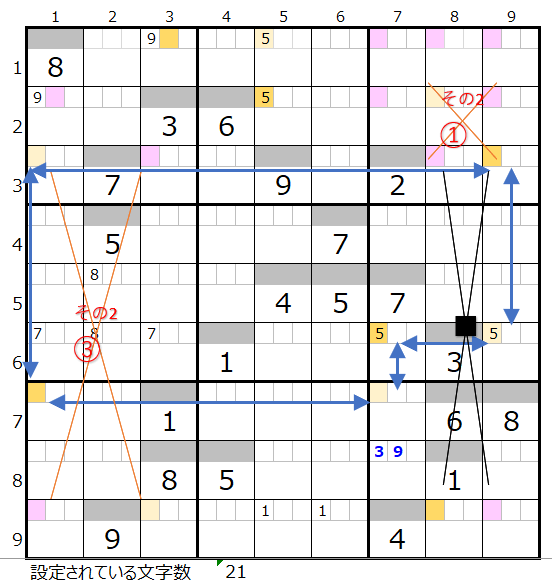
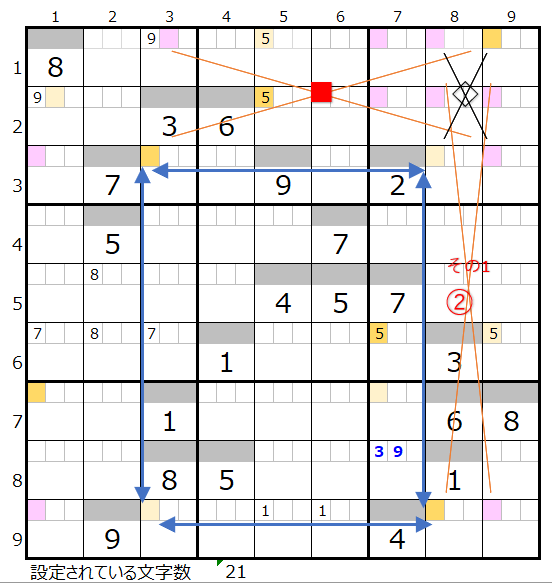
これはスクウェアができるため対象外となります。
実はこの形は「その1」の②の対角の場合になりす。
なお新たに◇の対角が現れるので確認します。
「その2」の③の対角が上右図になりますが、これも左と同様な不成立のケースとなります。
最後に、「その2」の①と③同時に対角を取った場合が左図になりますが、別のループができるため対象外となります。
なお新たに■の対角が現れますが、これは「その1」で既にご説明済みの形となります。
以上で一通りすべての連鎖について確認ができた認識です。
②複製連鎖で共通して通過するマス目を調べる
調べた結果として「その1」で2つ、「その2」で2つ、「その3」で1つ合計で5つの「成立する」連鎖のパターンがあることが解りました。
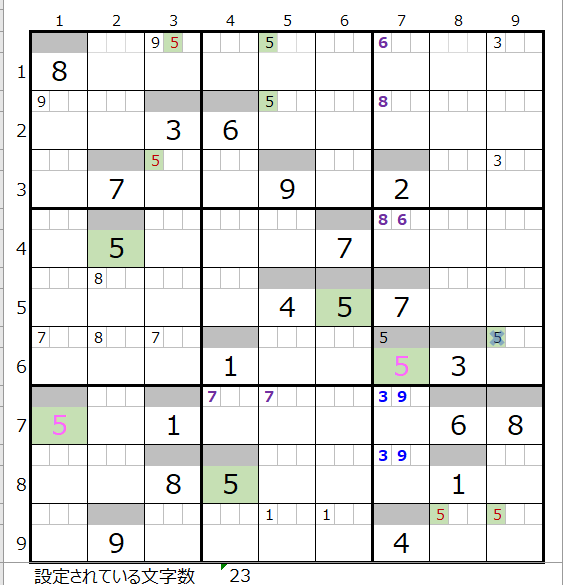
5つの連鎖が共通して通過するマス目を調べると左図で背景色を付けたマス目で「濃い」2か所、「薄い」で2か所あることが解ります。
なお今回の共通箇所は第14回でご説明した「共通して通過するマス目の中にスクウェアになり得る箇所が存在する」特異点は含まれていません。
従いましてこの「濃い」「薄い」どちらかに正解が存在しているはずですので、次に二択分岐をすることになります。
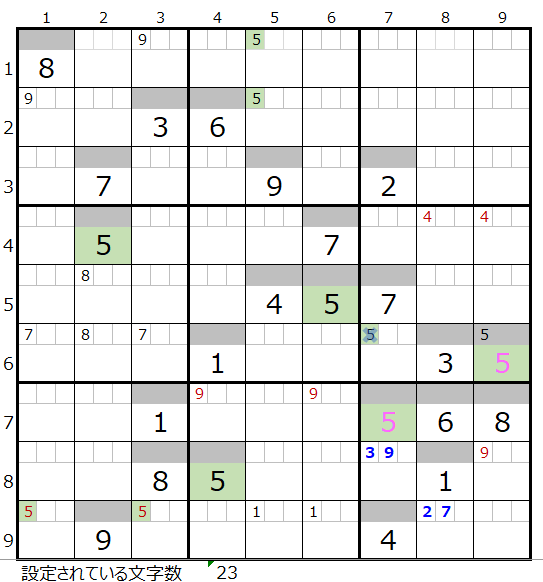
「濃い」「5」の盤面
文字色がピンク色の2か所が仮置きされたが、解法その1からその3では新たに数字が決まらずに行き詰った状態です。
「薄い」「5」の盤面
文字色がピンク色の2か所が仮置きされましたが、解法その1からその3では新たに数字が決まらずに行き詰った状態です。
まとめ
まだまだ初期の段階ではありますが、今回は最初の二択分岐が確定したところまでをご説明板ました。
次回はまず『「薄い」「5」』のその先についてご説明したく存じます。
最後までご一読いただき誠にありがとうございました。
