前回第12回では「色分け手法」の中の「色分の正誤を判断するための手法」により明確な差が出来るパターンでについてはご説明いたしました。
前回は経験則通りに行ったパターンでしたが今回は相反する結果になる例を、文字数「50」残り5ブロックのケースでご紹介したく存じます。
今回の説明で使用する数独問題について
今回もいままでと同じく下記サイトの2015年11月の問題集を使用させていただいています。
今回の問題は「数独問題集(達人級)」の2015/11/10上段に掲載されています。
これまでと同様に途中から使用させていただいておりますが、コピーライトは問題を作られている数独無料問題集様がお持ちのものになりますので初期の盤面につきましては、上記サイトにてご確認いただけますようお願い申し上げます。
「解法その3」終了時の盤面
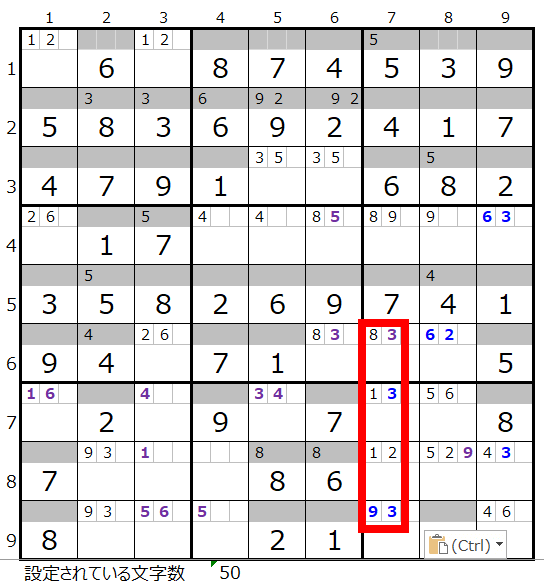
解法その1から3により文字数は50文字まで解かれていますが、本解法では盤面として行き詰まった状態です。
左図のメモ欄
・黒字—解法その1からセット
・太紫—解法その2からセット
・太青—解法その3からセット
特異点としては赤線枠で縦に数字「3」が3つ並んでいるところですが、次の章でご説明しますが今回数字「3」難易度が一番高いので対象となりません。
それ以外での特異点はありません。
メモ欄にセットされている数字の状況を1~9すべて確認する
第9回でご説明した「色分け手法」の手順に従い、ブロックに入る可能性のある箇所のメモ欄の背景色を薄ピンクにセットして行きます。
※数字の「7」は9ブロックすべてにセットが完了しているので画面ショットは省略致します。
なお説明のために可能性のある箇所の個数を数えていますが、ざっくりと難易度だけ把握すれば大丈夫です。
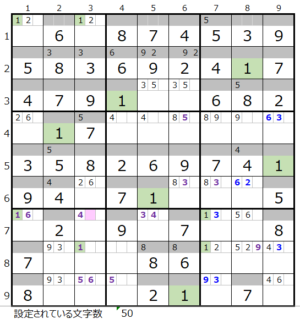 数字「1」–1ヶ所
数字「1」–1ヶ所
残り3ブロックなので後回し
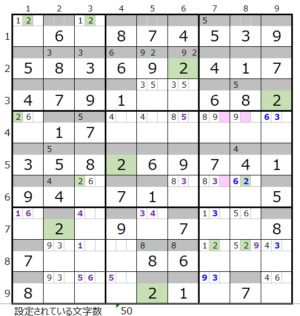
数字「2」–3ヶ所
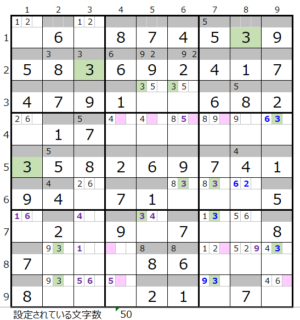
数字「3」–8ヶ所
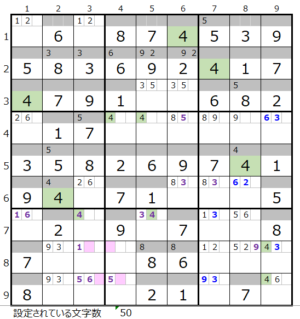
数字「4」–4ヶ所
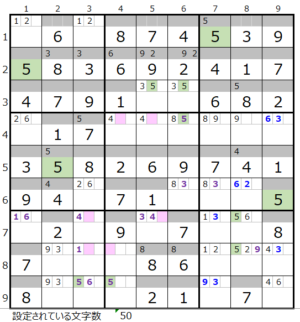
数字「5」–6ヶ所
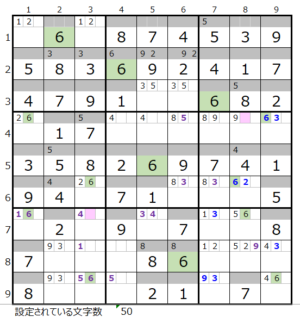
数字「6」–2ヶ所
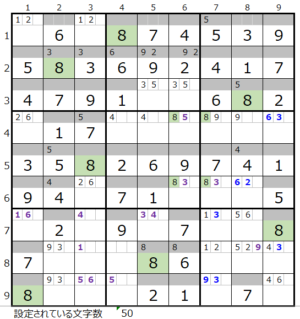 数字「8」–ゼロヶ所
数字「8」–ゼロヶ所

数字「9」–1ヶ所
残り3ブロックなので後回し
難易度の低い数字の連鎖を考える
今回の問題では設定されている文字数が「50」となっているので盤面的にはかなり煮詰まってきている状態です。
数字「1」と「9」は残り3ブロックなので後回しになります。
ブロックに入る可能性のある箇所が少ない数字を下から選ぶと対象となる候補は「6–2ヶ所」「2–3ヶ所」「4–4ヶ所」「5–6ヶ所」になります。
数字「5」が対象になっている理由は後段でご説明致しますが、今回は数字「2」と「4」を先に確認して行きます。
①数字「2」で連鎖を考える
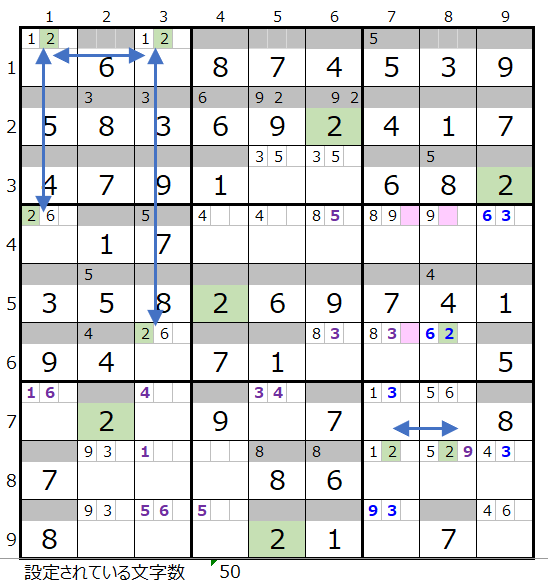
数字「2」は4ブロックですが、第1、第4ブロックは2ヶ所確定なので、残りの2ブロックをどのように通るか?になります。
残念ながら下記のように色分けは正しい2つのルートが存在しますので対象から外れます。
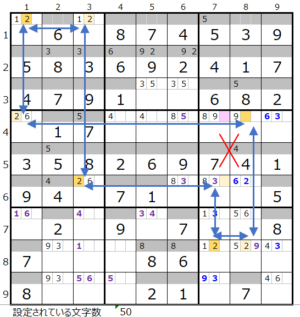 連鎖その1
連鎖その1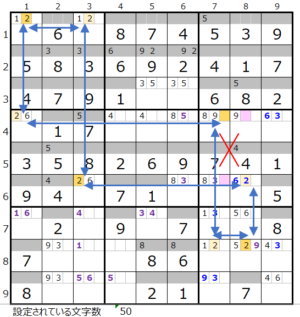 連鎖その2
連鎖その2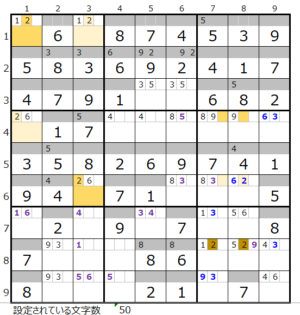 上図で背景色が付いたマス目は、2つの連鎖で共通に通過する箇所です。
上図で背景色が付いたマス目は、2つの連鎖で共通に通過する箇所です。
この「濃い」「薄い」のどちらかに今回は正解のルートが含まれています。
複数連鎖が存在する場合の対処法につきましては次回ご説明いたしますが、複数連鎖で共通して通過するマス目の「濃い」「薄い」のどちらかに正解のルートが含まれているケースがあることが解ります。
②数字「4」で連鎖を考える
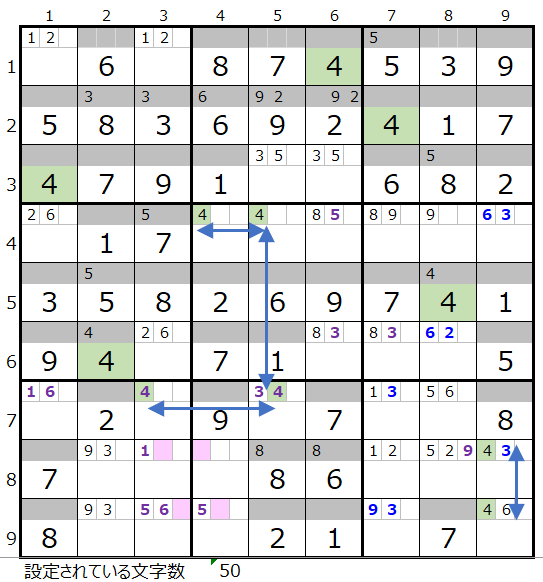
数字「4」は4ブロックですが、第5、第9ブロックは2ヶ所確定なので、残りの2ブロックをどのように通るか?になります。
これも残念ながら下記のように色分けは正しい2つのルートが存在しますので対象から外れます。
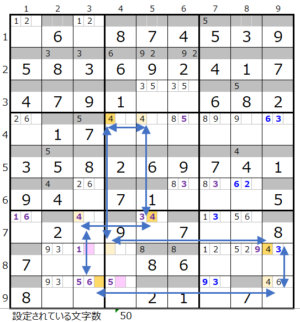 連鎖その1
連鎖その1
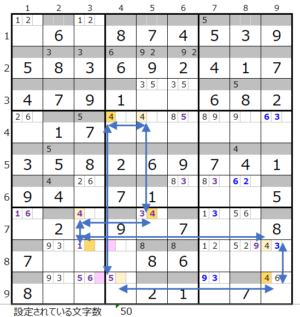 連鎖その2
連鎖その2
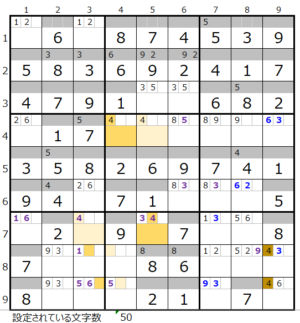 上図で背景色が付いたマス目は、2つの連鎖で共通に通過する箇所です。
上図で背景色が付いたマス目は、2つの連鎖で共通に通過する箇所です。
この「濃い」「薄い」のどちらかに今回は正解のルートが含まれています。
このように4つの候補の内の2つが連鎖がユニークではないために候補から外れてしまいました。
そのために最初から背景色薄ピンク色が6ヶ所の数字「5」を加えていたのですが、それにもまして今回のテーマである「色分の正誤を判断するための手法」で相反する結果になるのが数字「5」の場合だからになります。
それでは数字「6」よりも先に数字「5」を確認して行きます。
③数字「5」で連鎖を考える
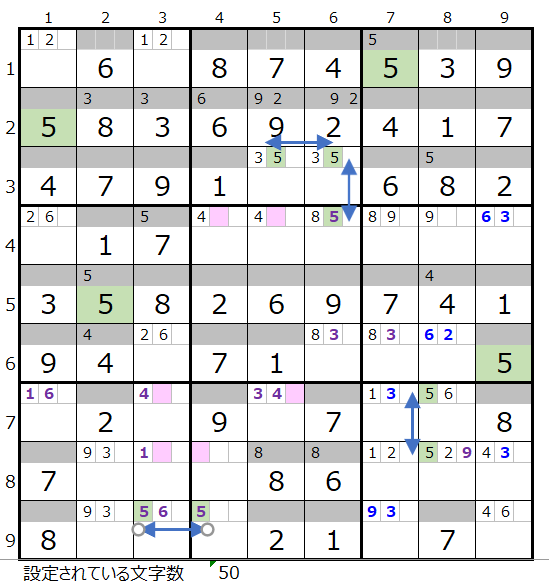
数字「5」は残り5ブロックでのケースになります。
第2ブロックと第5ブロック、第7ブロックと第8ブロックにスクウェアになり得る箇所があるため、それを回避しつつ第9ブロックを通過するルートを考えるとなるとかな選択肢は絞られます。
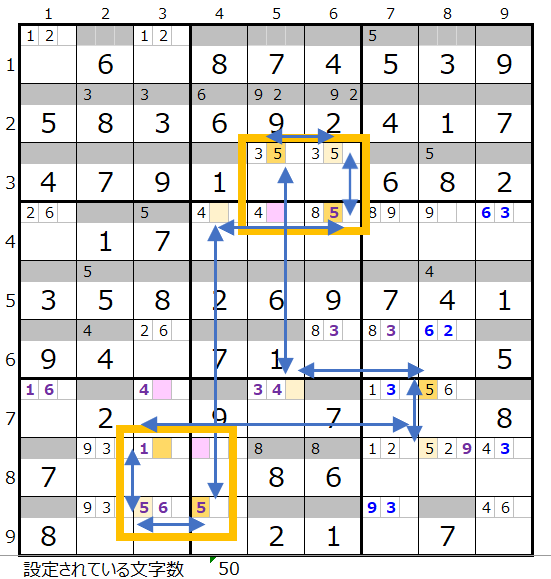
黄枠の2か所がスクウェアになり得るところですが、それを回避しつつ残り5ブロックをすべて通過する連鎖としてはこれしかない認識です。
一応ユニークで色分けも正しい連鎖ですかので次のステップに移る候補になります。
④数字「6」で連鎖を考える
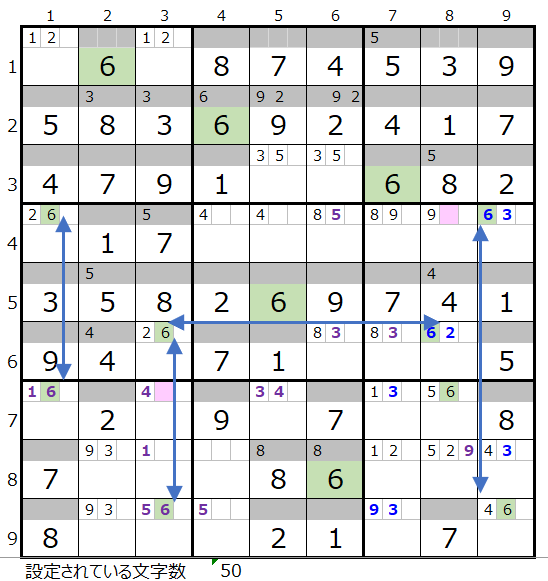
残り4ブロックですが、第4ブロックと第9ブロックはメモ欄の位置が確定しているため自由度がありません。
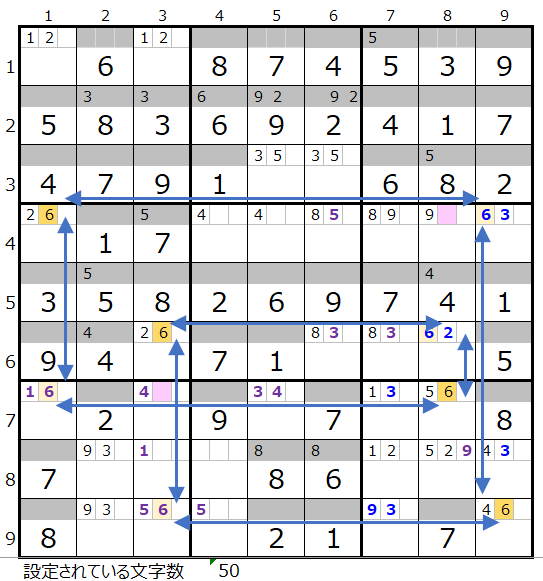
残りすべてのブロックを通過するルートとしては左図しか存在しない認識です。
ただし色分けして見ると残念ながら成立していません。
つまり4ブロックすべてを通過する連鎖は作れない事が解りました。
そうなりますとどこか他のブロックに影響を与えないブロックを切り離して3ブロックでの連鎖に変更することになります。
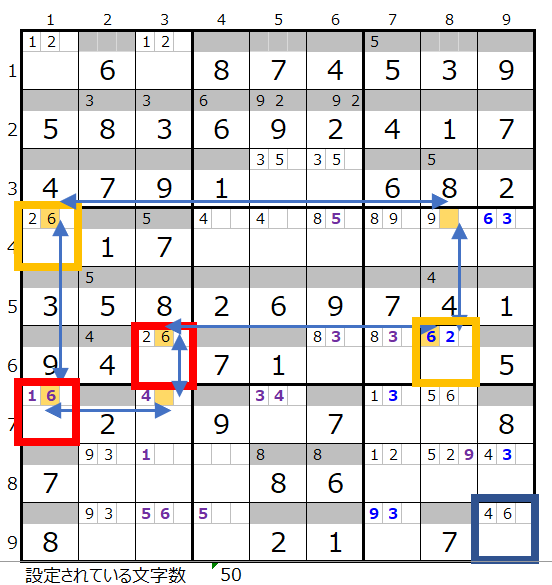
切り離す候補としては自由度が無い第4ブロックか第9ブロックになりますが、第4ブロックの黄枠を確定されると、第6ブロックの黄枠が決まってしまいます。
同様に赤枠を確定されると第7ブロックの赤枠が決まってしまいます。
つまり第4ブロックだけを切り離すことはできません。
そうなりますと切り離すのは第9ブロックの紺枠となり、残り3ブロックでの連鎖は左図になりこれしか存在しません。
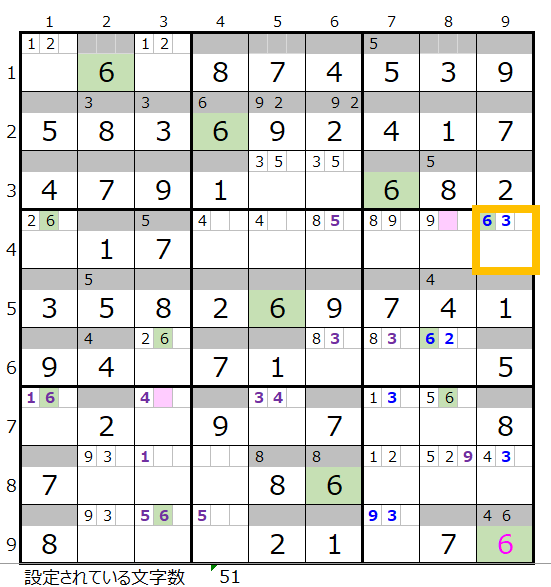
残り3ブロックの連鎖はさておき左図のように9行9列に「6」が入ると、黄枠は解法その3でセットされているため「3」になることが確定します。
すると9列目はすべて埋まることになりまが、その先は是非皆さまでご確認をいただければ幸いです。
「色分の正誤を判断するための手法」を使う
ここまでで、難易度の低い数字の連鎖は全て調べ終わりましたので、次のステップである「色分の正誤を判断するための手法」に移ります。
条件としては連鎖がユニークである必要があり、残り3ブロックについては後回しになりますので今回対象となるのは「5」だけになります。
数字「5」を調べる
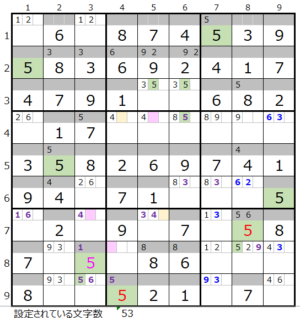
第7ブロック→第9ブロック→第8ブロック
カウントは「濃い」3/5
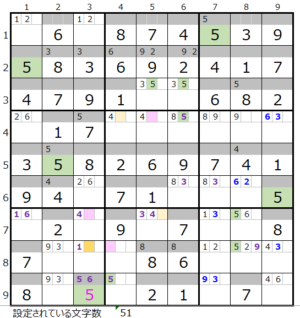
第7ブロック
カウントは無し(薄い)
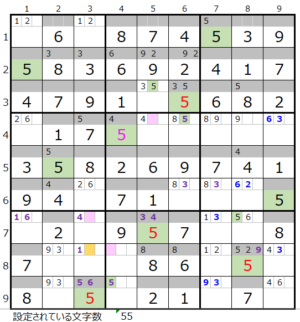
第5ブロック→第8ブロック→第2ブロック→第9ブロック→第7ブロック
カウントは「薄い」1
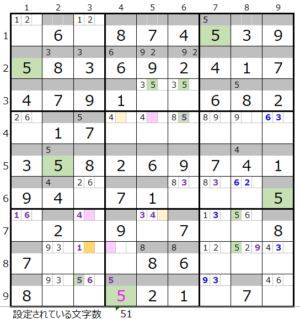
第8ブロック
カウントは無し(濃い)
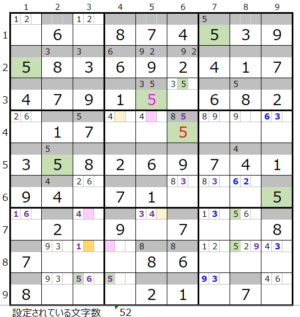
第2ブロック→第5ブロック
カウントは無し
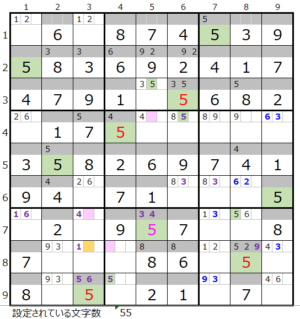
第8ブロック→第9ブロック→第2ブロック→第5ブロック→第7ブロック
カウントは「薄い」1
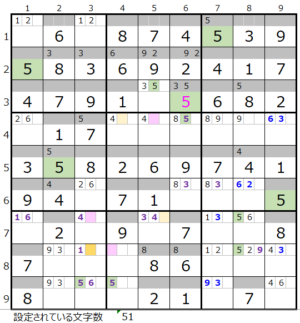
第2ブロック
カウントは無し(薄い)
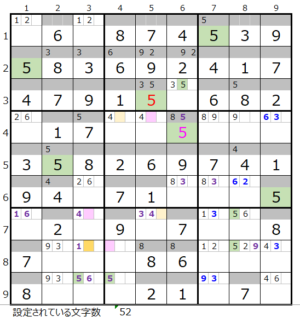
第5ブロック→第2ブロック
カウントは無し
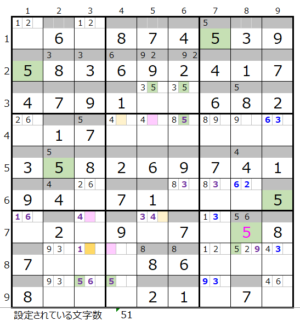
第9ブロック
カウントは無し(濃い)
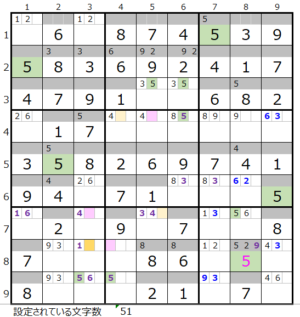
第9ブロック
カウントは無し(薄い)
以上により、カウントの結果としては
・濃い—3/5
・薄い—1,1
となり、「薄い」が「1と2/5」大きい結果となりました。
ただし「 仮置きしたマス目以外は解けない 」個数は
・濃い—2ヶ所
・薄い—3ヶ所
となり、この結果からは少ない方である「濃い」を選択することになります。
つまり2つの結果が相反することになります。
となりますと経験則は適用できませんので、まずは「薄い」を選択し二択分岐をしてみます。
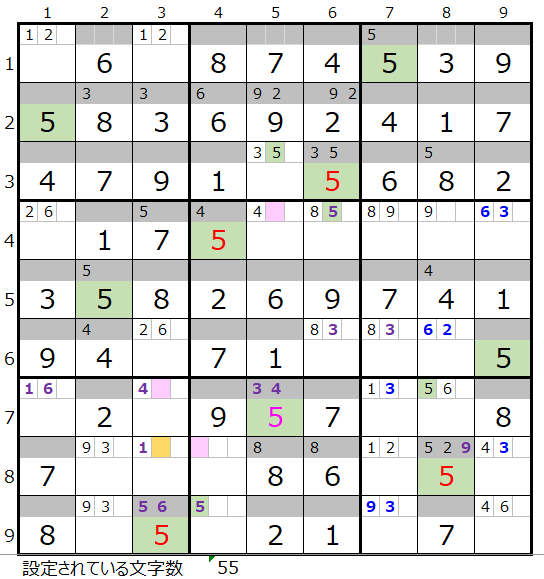
左図のように5がすべて埋まったところからスタートします。
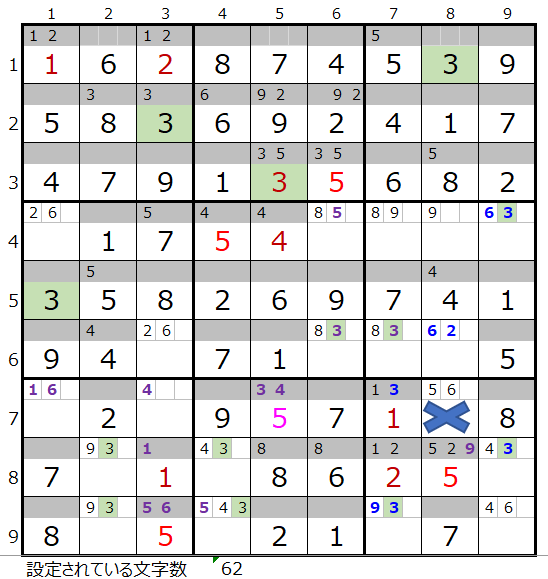
ただしこの場合はほどなく不正解であることが解ります。
左図では「5」の配置場所と7行7列に「1」が入った関係で7列目に「3」が入らない状態になっています。
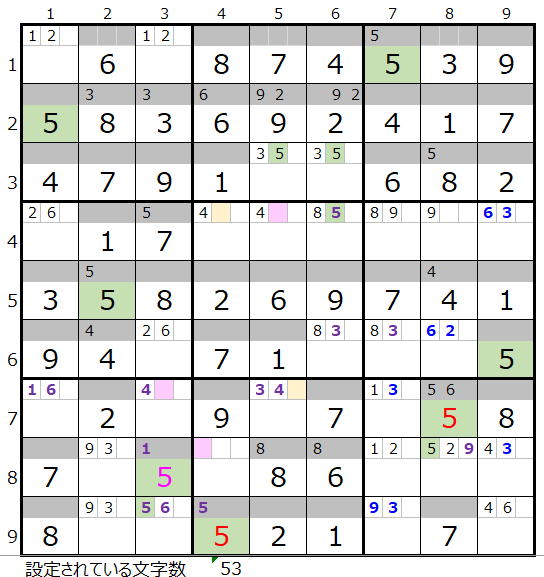
そこでもう一つの選択肢である「濃い」3/5の左図からスタートしてみます。
なおお手数ではありますが、この先につきましては皆様でご確認をいただければ幸いです。
なお7行8列に「5」が入ると数字「6」が9行9列に決まります。
実はこれは数字「6」に出てきた状態と同じになります。
まとめ
今回は残り5ブロックで「色分の正誤を判断するための手法」により明確な差が出来るパターンで結果が異なるケースをご紹介しましたが、今回の数字「5」のケースのようにスクウェアになり得るところを回避した連鎖になっている時はカウントの合計と「 仮置きしたマス目以外は解けない 」個数が相反する結果になり得ますので注意が必要です。
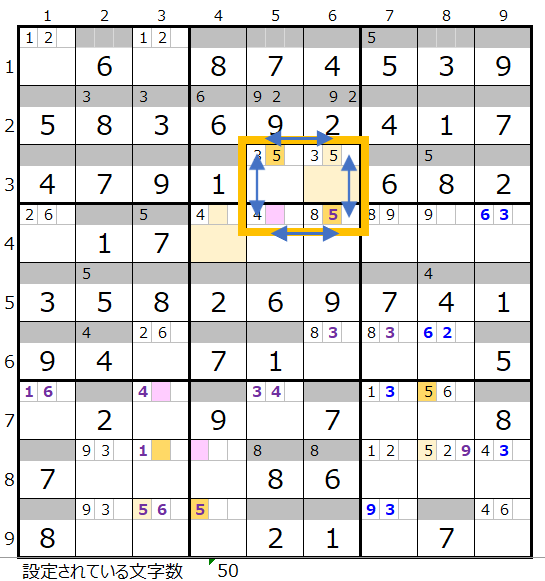
もしもスクウェアが正解だった場合は、連鎖はスクウェアを回避しているので左図で「薄い」は黄枠の外にあり正解を捕らえていません。
「色分の正誤を判断するための手法」により今回は「濃い」3/5の仮置きではこのスクウェアのリスクを取り除いたマス目を示してくれています。
なお『「色分けの手法」が必ずこのようなリスクを排除してくれるのか?』という疑問につきましてはすべての数独の問題を確認したわけではないので大変恐縮ではありますが「経験則的には排除してくれる」という回答にならざるを得ない認識です。
次回は複数連鎖がある場合の対処法をご紹介したく存じます。
以上、最後までご一読いただきありがとうございました。

