「数独向けの条件付き書式とは何ですか?」の記事を書いてから、2ヵ月半が過ぎてしまいました。
その間、会社会計処理の対応や、Google Adsenseへの対応、書式作成や「知ってたら得するかもしれないExcelの癖」シリーズの記事作成などいろいろな事がありましたが、ご案内から随分と時間がかかってしまいましたことご容赦ください。
数独を解く時のスタンス
前回「世界SUDOKU(ナンプレ)選手権」が開催されている話題を取り上げましたが、世の中で数独を極めるとすると下記の2つのスタンスになる認識です。
- 短い時間で解答を見つける
- 難しい数独の解答を見つける
本書式を利用する場合のスタンスは後者の方になります。
ただ「難しい数独」と言われると、「初心者が手を出すものではない」もののように思われるかもしれませんが、実際に解いてみた範囲では別に難しい解法を知らなくても、基本的な解き方さえ間違えなく解っていて正しく使うことができれば、時間はかかるかもしれませんが、最終的には正解にたどり着けくことができるものであると信じています。
なお、「別に極める必要など無い」と考えている方もいらっしゃることと存じますが、ただ「ほんの少しの労力」で「玄人(くろうと)向けの問題を解く」という楽しみを享受することができると思いますので、是非一度チェレンジされることをお勧めいたします。
世界一難しい数独
話は変わりますが「世界一難しい数独」というものをご存知でしょうか?
ただし話題としては随分昔の、9年弱前の話にはなります。
ネットで調べてみると2010/8/22日にひとつ掲載されています。
それから2年弱後の2012/7/3日にも掲載されています。
ただしどちらも、作成者といいますか出どころは一緒で、フィンランド人の環境科学者(後者では数学者)のArto Inkala博士が手がけた数独作成プログラムにより作成されているようです。
後者の問題は既にネット上ではいろいろな解法例が掲載されていますし、本書式作成時に試した解法である、「二択分岐する点を探して、実際に数字を埋めて解答に辿り着けるかを地道に確認する方法」による解答例も散見されますので、いまさら解法を載せることに新鮮味はありません。
とはいうものの、会社として記事にするにあたり「本当にすべて試したの?」とか「解答を見れば、二択分岐する点でどちらを選ぶか分かるのでは?」などの指摘を受けた時に、「ちゃんと調べたという証拠をお示しする必要がある」と考えまして、すべての分岐を確認して掲載することにしました。
この「すべての分岐掲載する」という点につきましては、面白みはありませんが少しだけ新鮮味はあることと存じます。
その結果は弊社の∞ワークスSTORE「世界一難しい数独で仮置きしたすべての分岐を調べた結果(リスト)」で掲載していますが、同じものを下記に掲載いたします。
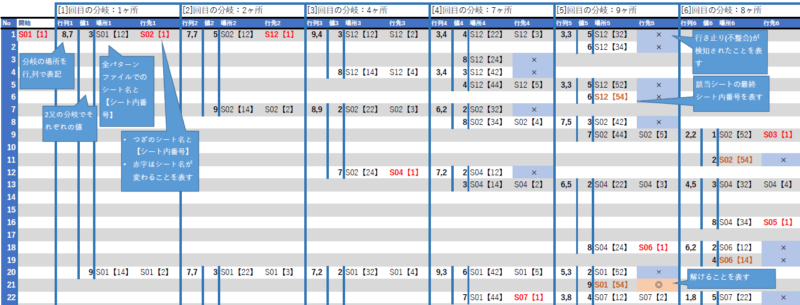
表の見方としては、左上隅から始まり、見出し行の右方向に1回目、2回目…と分岐の回数を表示しています。
見出し行の中で、場所と行先の赤文字は別コンテンツのための情報になりますので無視していただければ幸いです。
この表におけるメインの情報は、行列と値の見出しになります。
例えばNo「1」の行の左上隅の行列1は「8,7」で値1は「3」になっています。これが意味するところは、8行3列のマス目に二択分岐で値「3」を仮置きして解き進めるた場合に、右隣の行列2で更に7行7列のマス目に二択分岐で値「5」を仮置きして…、以降解けるか行き詰るまでの二択分岐ルートを表しています。
ちにみに解答にたどり着くまでの二択分岐ルートは下記のようになります。
- 8行7列のマス目に値「9」
- 7行7列のマス目に値「3」
- 7行2列のマス目に値「2」
- 9行3列のマス目に値「6」
- 5行3列のマス目に値「9」
なお、この確認と上記資料のまとめには今年1月の0.5人月ぐらいの工数を要しました。
といいますか、できないパターンを検証する時のデジャヴ(既視感)と、分岐点に戻る時の手戻り感はとてもダメージが大きくて、すべての確認が終わった後しばらくは数独に触れるのが厭われました。
このことは冒頭の本記事の作成までに時間がかかった理由には含めていませんが、要因のひとつではあります。
難しい数独を解く時の手段
書式はExcelを使用しているので、Excelのマクロ(VBA)を使用した解答補助機能を期待されるかもしれませんが、本書式は解答を得るためのコンピュータ処理は行っておりません。
デジタルではなく、アナログで解くことで「脳を活性化する」ことができると信じています。
そして解くに当たり「特定のマス目にセットできる数字の数をいくつまで考慮すべきか?」悩むところですが、本書式では基本は2つまでにします。
「なぜ2つか?」というと2つであれば、白と黒なので何とかアナログでも対応できると思えるからです。
これが3つとなると、白、黒、グレーとなり考慮しなければならないことが増えてしまいます。
確かに3つまで追わないと見つけられないケースもあることと存じます。
(この件につきましては、今後時間をいただきあらためて確認を致します。)
ただ時間は気にしないのであれば、2つの場合でも、二択分岐による仮置き回数を増やすことで解決できるものと考えます。
しかしそうは言いながら、安直に二択分岐の回数を増やすのは良くないことと存じます。
二択分岐はあくまでも「試行錯誤が行き詰った時の最終手段」である認識です。
書式を使った数独の解き方
その前に4つだけ用語の使い方を整理しておきたく存じます。
| マス目 | 9行(横方向)×9列(縦方向)の数独には81個のマス目があります。Excel的な表現をすると「セル」になります。 |
| ブロック | 3行(横方向)×3列(縦方向)のくくりで、9行(横方向)×9列(縦方向)の数独には9つのブロックがあります。 |
| ターゲット | 特定したい数字を表します。場所ではありませんのでご注意ください。 |
| 狙い目 | ターゲットをセットするマス目を表します。数字ではありませんのでご注意ください。 |
- ターゲット(特定したい数字)を行(横方向)と列(縦方向)の2方向で探し、ターゲットを含まないブロックで狙い目(ターゲットをセットできるマス目)を見つけます。
- 狙い目が1つしかなければ、その狙い目にターゲットをセットします。
- 狙い目が2つの場合はメモ欄にターゲットをセットします。
- 狙い目が3つ以上の場合は、何もしません。
※この作業は、数独の解法としては基本的なものになりますが、「このパターンは知っていた方が良い」というものが3つ4つありますので、別の回でご説明いたします。
- 行(横方向)または列(縦方向)で、1方向でターゲットを探し、ターゲットを含まないブロックで狙い目を見つけます。
- ひとつの行または列で狙い目が1つしかなければ、その狙い目にターゲットをセットします。
- ひとつの行または列で狙い目が2つの場合はメモ欄にターゲットをセットします。
- 狙い目が3つ以上の場合は、何もしません。
※「解法その1」からブロックの考慮を(2019/8/29誤記訂正)1方向を取り除いた解法です。狙い目が1つしかないというのはレアケースにはなりますが、その後の展開でも使用する解法になります。詳細は別の回でご説明いたします。
- ターゲットは決めずに、狙い目だけ特定して、行(横方向)、列(縦方向)、ブロックの状態から、狙い目に入る数字を1から順に確認して行きます。
- 「1から9」で入る数字が1つしかなければ、その数字を狙い目にセットします。
- 入る数字が2つの場合はメモ欄にターゲットをセットします。
- 入る数字が3つ以上の場合は、何もしません。
※これも数字が1つしかないというのはレアケースになりますが、これも先ほどと同様に、その後の展開でも使用する解法になります。詳細は別の回でご説明いたします。
まとめ
上記の解法につきましては、どれも基本的なものばかりになりますが、上記3つの解法を使っても解答にたどり着けず行き詰ってしまった時に、二択分岐をすることになります。
その際にターゲットが2つだけになるマス目を探す必要がありますが、マス目の数が少ない場合は、2~3手先を確認してから、どれか一つを選択することになりますが、ターゲットが2つのマス目のベーアが複数あるような場合は「どこのペアにするのが良いか?」を決める必要がある認識です。
その際に使用する「解法その4」があるのですが、それは別な回でご説明いたしたく存じます。
以上、最後までご一読いただきありがとうございました。
2019/8/28追記
当初は3つの解法で解答にたどり着けない場合は二択分岐をすることを前提にしていましたが、ここにきて「二択分岐はなるべく使わない形で解けないか?」「その場合にはどのような書式が良いか?」という形で見直しを進めています。
二択分岐を使用しない意図としましては、やはり解けないバターンの場合の手戻り感と、行き詰った時の「やるせなさ」を回避したいという思いからです。
そのため「解法その4」の見直しを現在していますが、ただ正直なところ「二択分岐をまったく使わない」訳ではなく、また解法というほどセオリー通りに解けるものでもなく、「こんな風に考えていくと解答に向けた道筋が見えてくる」といった感じのものになります。
内容につきましては近々記事でご紹介させていただく予定です。
ちなみにどういった場合に二択分岐が必要になるか?と言いますと、解法その3までで行き詰った時点で、盤面にある数字の数が40前半以下の場合になります。
これはおそらく本解法が「メモ欄にセットするのは、基本狙い目2つまで」にしていることのに起因する認識ですが、そうではありますが、いましばらくは上記の解法を崩さないで置きたく存じます。
(この理由としては、ここを見直しするとなると年単位で時間がかかる認識のためです…)
何卒よろしくお願い申し上げます。