これまでの「色分けの手法」のご説明では「連鎖がユニーク」の場合だけに限っていましたが、今回は複数連鎖がある場合の対処法につきましてご説明したく存じます。
第11回で記載しているように「同じ数字で連鎖が複数ある場合には残念ながら対応できる場合とできない場合があります」が、「どのような場合に対応できないのか?」につきましては経験則からご説明して参ります。
今回の説明で使用する数独問題について
今回もいままでと同じく下記サイトの2015年11月の問題集を使用させていただいています。
今回の問題は「数独問題集(達人級)」の2015/11/24日上段に掲載されています。
これまでと同様に途中から使用させていただいておりますが、コピーライトは問題を作られている数独無料問題集様がお持ちのものになりますので初期の盤面につきましては、上記サイトにてご確認いただけますようお願い申し上げます。
なお「連鎖がユニーク」となる数字が1から9の中に1つも存在しないという問題は「難しい数独」の中でもかなり難易度が高い問題であることが想定されますしさほど見かける事がありませんので、「連鎖がユニーク」である数字と複数連鎖となる数字が両方存在する問題を使用しています。
「解法その3」終了時の盤面
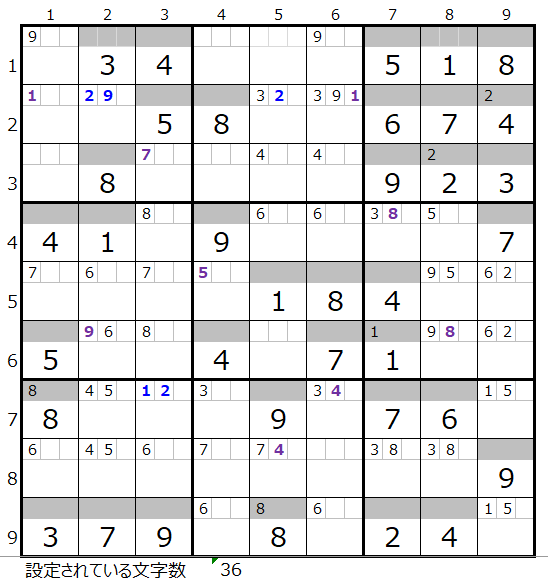
解法その1から3により文字数は36文字まで解かれていますが、本解法では盤面として行き詰まった状態です。
左図のメモ欄
・黒字—解法その1からセット
・太紫—解法その2からセット
・太青—解法その3からセット
特異点はありません。
メモ欄にセットされている数字の状況を1～9すべて確認する
第9回でご説明した「色分け手法」の手順に従い、ブロックに入る可能性のある箇所のメモ欄の背景色を薄ピンクにセットして行きます。
なお説明のために可能性のある箇所の個数を数えていますが、ざっくりと難易度だけ把握すれば大丈夫です。
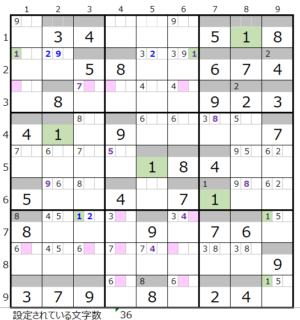数字「1」–12ヶ所
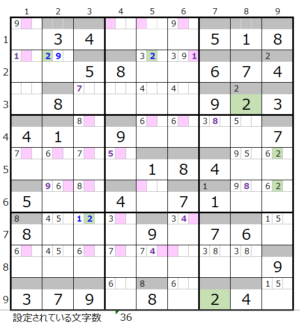
数字「2」–23ヶ所
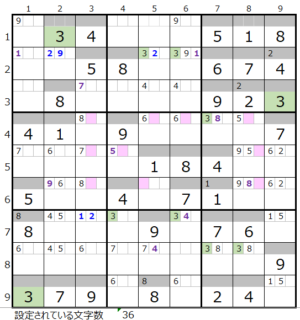
数字「3」–10ヶ所
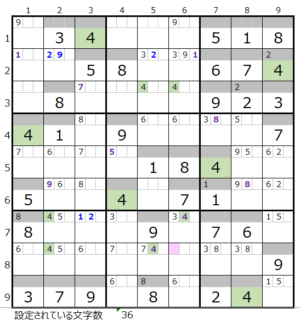
数字「4」–1ヶ所
残り3ブロックなので後回し
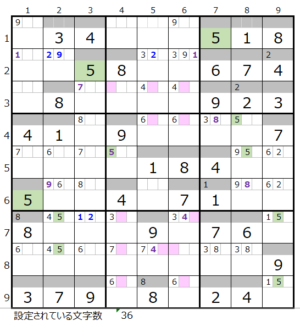
数字「5」–12ヶ所
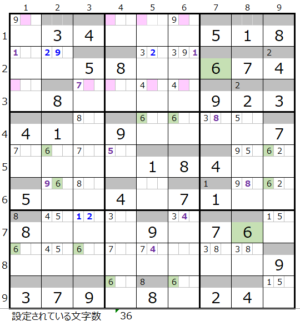
数字「6」–9ヶ所
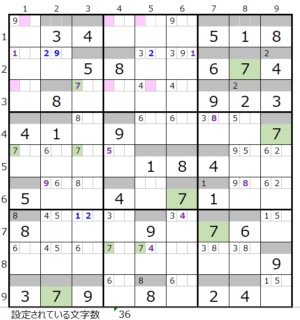数字「7」–6ヶ所
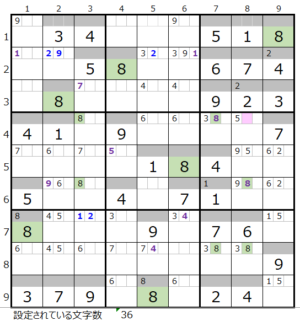
数字「8」–1ヶ所
残り3ブロックなので後回し
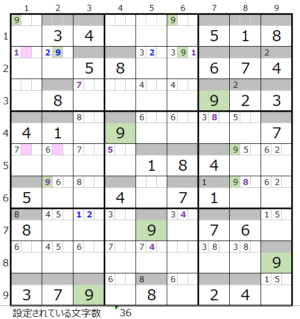
数字「9」–3ヶ所
難易度の低い数字の連鎖を考える
「色分けの手法」においては難易度の低い数字で連鎖を考えてユニークな連鎖を探し出すのが基本的なスタイルです。
その際に残り3ブロックになる数字は後回しになります。
そうなりますと、数字の「2」は背景色薄ピンク色の箇所が「23か所」あるので対象外とし、まだ数字「4」と「8」は残り3ブロックなのでこれも後回しとなります。
ブロックに入る可能性のある箇所が少ない数字を下から選ぶと対象となる候補は「9–3ヶ所」「7–6ヶ所」「6–9ヶ所」「3–10ヶ所」になりますのでこの順番で確認して行くことにします。
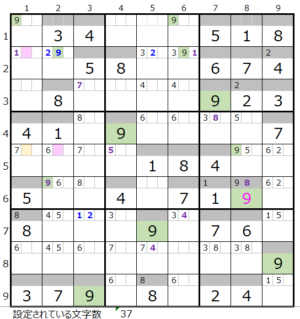
①数字「9」で連鎖を考える
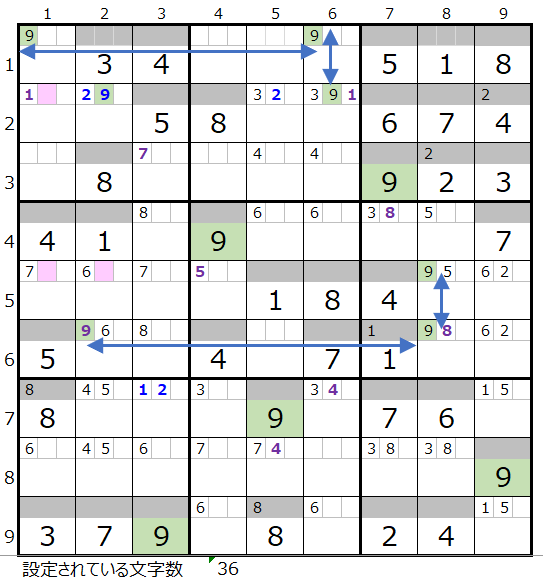
数字「9」は残り4ブロックですが、第2、第6ブロックは2ヶ所確定なので、残りの2ブロックをどのように通るか?になります。
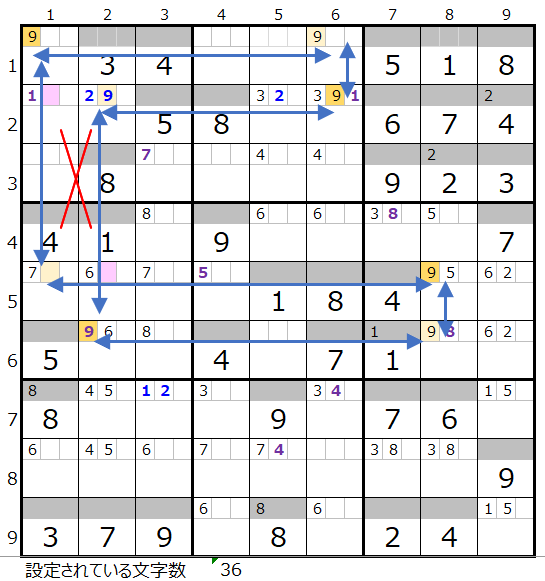
連鎖としては左図のルートが色分けも正しいので一つ考えられますが、赤×印のところが対角線での置き換えが可能な形です。
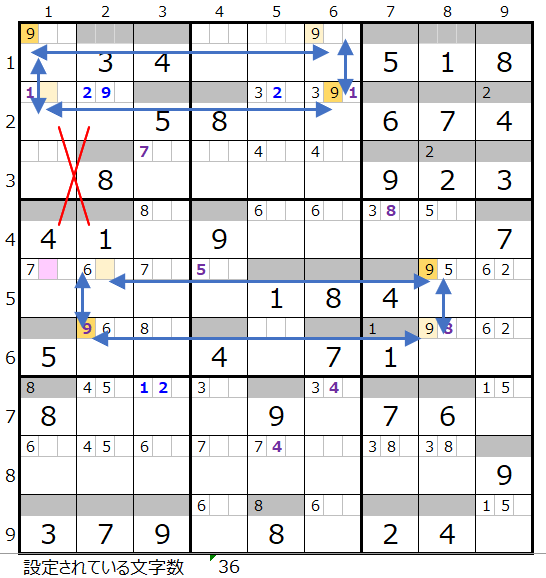
ただし置き換えてみると、2つのスクウェアができて連鎖が2つのパターンになってしまうため、残り全てのブロックを通過する連鎖としては上図しかないようです。
なお今回の場合は残りのブロックが4つなので、「仮置きしたマス目以外は解けない」個数は有効ではありませんが、このようにスクウェアになり得るところを回避した連鎖は前回の第13回でも取り上げていますが連鎖を取るともしもスクウェアが正解だった時はスクウェアの逆のマス目はカバーできていない事をお含みおきいただければ幸いです。
「色分の正誤を判断するための手法」を使った結果は下記のようになります。
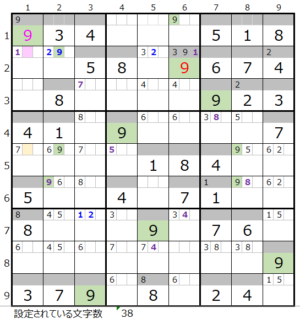
①第1ブロック→第2ブロック
カウントは「濃い」1/2
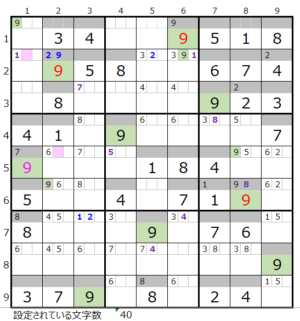②第4ブロック→第6ブロック→第1ブロック→第2ブロック
カウントは「薄い」1
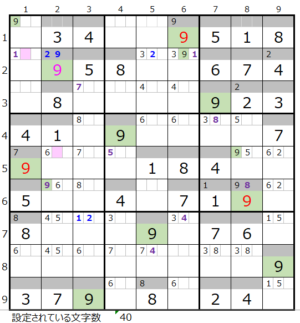
③第1ブロック→第2ブロック→第4ブロック→第6ブロック
カウントは「薄い」1
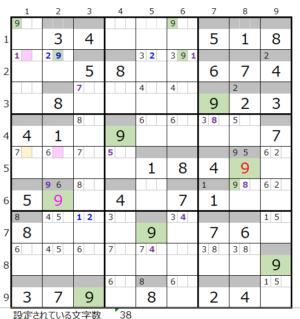
④第4ブロック→第6ブロック
カウントは「濃い」1/2
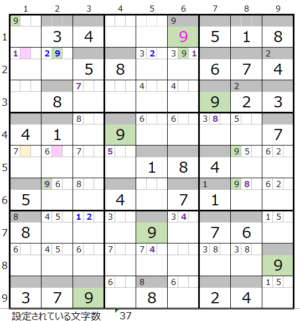
⑤第2ブロック
カウントは無し
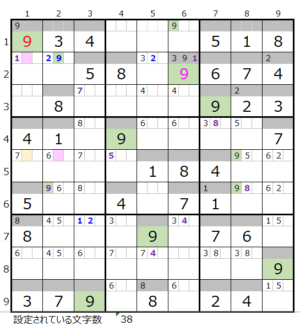
⑥第2ブロック→第1ブロック
カウントは「濃い」1/2
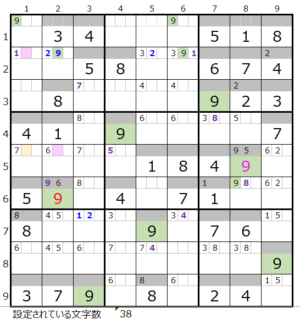
⑦第6ブロック→第4ブロック
カウントは「濃い」1/2
⑧第6ブロック
カウントは無し
以上により、カウントの結果としては
・濃い—1/2,1/2,1/2,1/2
・薄い—1,1
となり、両者が等しい結果となりました。
従いまして、「濃い」1/2の場合と「薄い」1の場合で二択分岐をすることになります。
なお「濃い」1/2は4つありますが、「第1ブロックと第2ブロック」「第4ブロックと第6ブロック」に入る2つのパターンがあります。数は両者2つづつです。
「第1ブロックと第2ブロック」の場合—第4ブロックと第6ブロックがスクウェアになる
「第4ブロックと第6ブロック」の場合—第1ブロックと第2ブロックがスクウェアになる
ことを示していると考えられますが、どちらも「濃い」ルートととしてむそれぞれのスクウェアに入っているのでどちらを選んでも大丈夫になる認識です。
盤面は省略されていただきますが二択分岐で「薄い」場合のパターンは少し解くと手詰まり(不正解)でありことが解ります。
「濃い」場合につきましては是非皆さまでご確認をいただければ幸いです。
②数字「7」で連鎖を考える
今回のメインテーマは「複数連鎖の対処法」でした。
実は残りの3つの数字は連鎖が複数存在する事例となります。
この中で対処法につきましてご説明したく存じます。
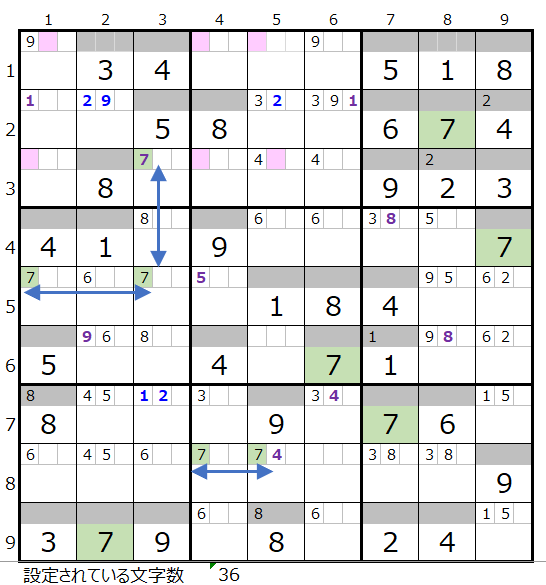
数字「7」は残り4ブロックですが、第4、第8ブロックは2ヶ所確定なので、残りの2ブロックをどのように通るか?になります。
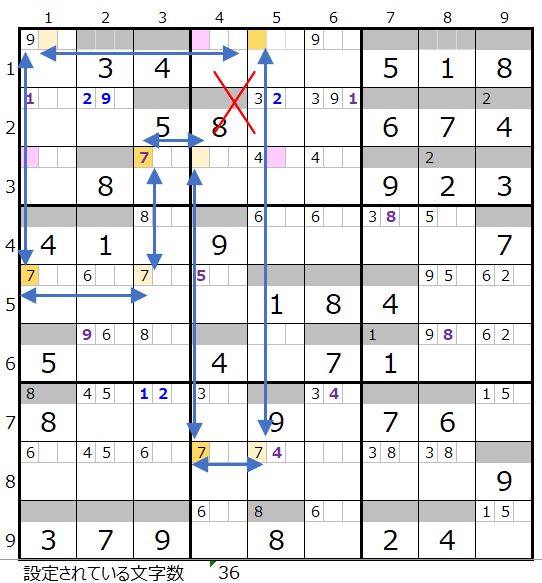
左図のような色分けも正しい連鎖がひとつ考えられます。
ただし赤×印のところは対角を通過するルートの存在が疑われます。
なお複数連鎖の場合は色分けの際に1点注意点がございます。
それは「どこのマス目から色分けを開始するか?」です。
今回の問題では第2ブロックに赤×印があり、その影響を色分けについては第8ブロックが受けます。
従いまして、このような影響を受けない第1ブロックか第2ブロックからスタートする必要があります。
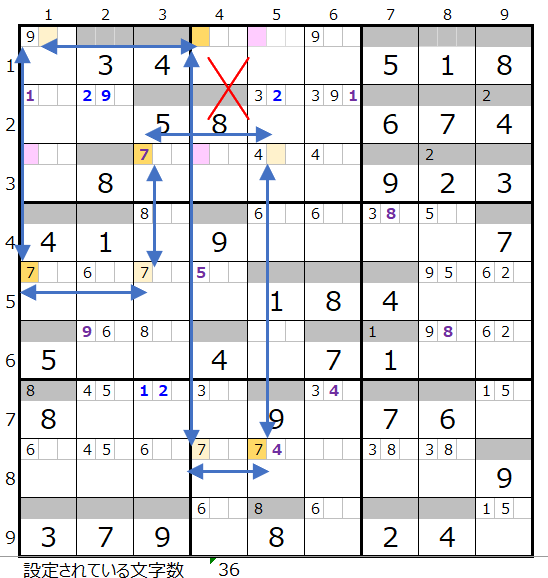
もしも第8ブロックから色分けをスタートしていたら色分けが同じで同じマス目を通過するポイントが第8ブロックだけになってしまいますので注意が必要です。
話を複数連鎖に戻しますとやはりもう一つ連鎖があることが解りました。
なおこれ以外には連鎖は存在しない認識です。
ここで色分けが同じで両者共通して通過するマス目を確認します。
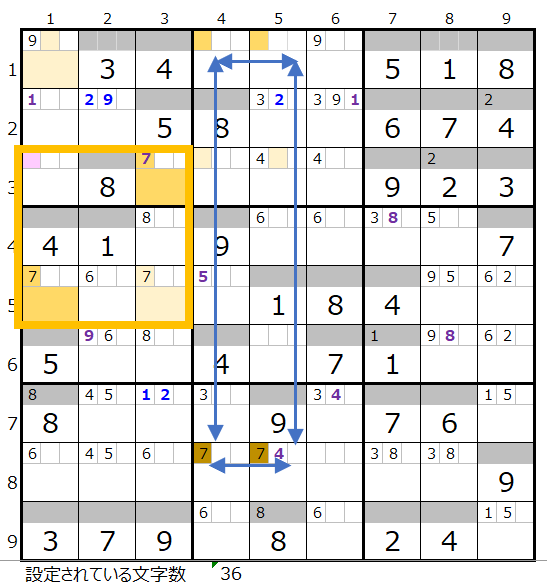
左図第1ブロックと第2ブロックにある背景色「濃い」「薄い」のそれぞれ2か所が色分けが同じで共通して通過するマス目になります。
ちなみに、数字「9」を解いて確認すると、この背景色「濃い」「薄い」のいづれかに正解が含まれている事が解ります。
ここから先は後段でご説明致します。
③数字「6」で連鎖を考える
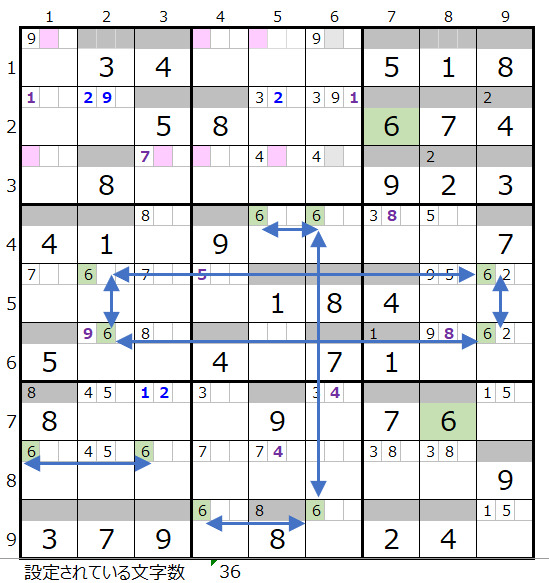
数字「6」は残り7ブロックでのケースになりますが、第4ブロックと第6ブロックにはスクウェアがあり、実施は残り5ブロックの状態です。
第1ブロックと第7ブロック、第2ブロックと第8ブロックにスクウェアになり得る箇所があるため、それを回避しつつ第5ブロックを通過するルートを考える必要があります。
なお第2ブロックの6列目が背景色薄ピンク色ではなく薄灰色のところがあります。
この理由は6列目は第5ブロックと第8ブロックがそれぞれ解法その1からメモ欄にセットされているのでこれ以上6列目に通過ポイントはありません。
そのため背景色を薄灰色にして候補地から外しています。
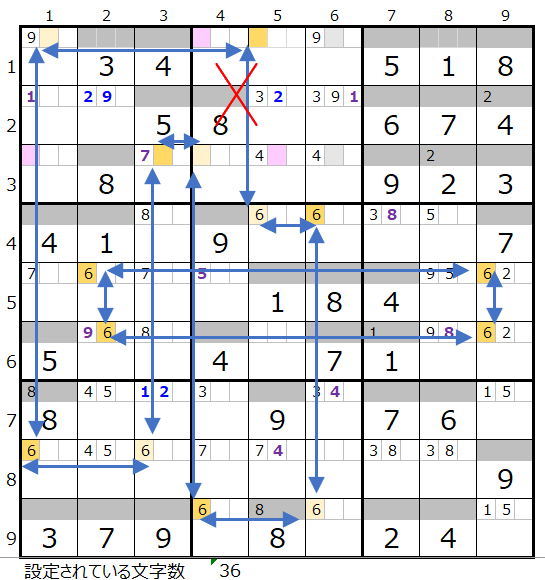
真ん中のスクウェアを除くと、先ほどの数字「7」と残りブロック数こそ1つ多いのですが赤×印の位置などが近しい配置になっています。
色分けが正しい連鎖がひとつ見つかりましたが、赤×印の箇所を確認する必要があります。
なお色分けは第1ブロックか第7ブロックからスタートするのが良さそうです。
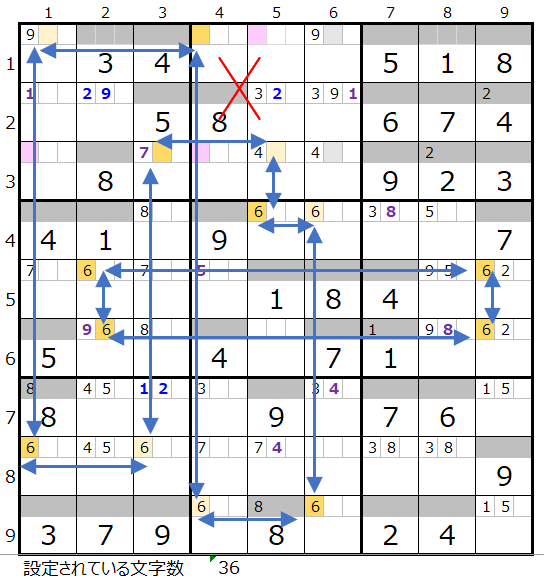
やはりもう一つの連鎖がありました。
ただしこれ以上は無い認識です。
ここで色分けが同じで両者共通して通過するマス目を確認します。
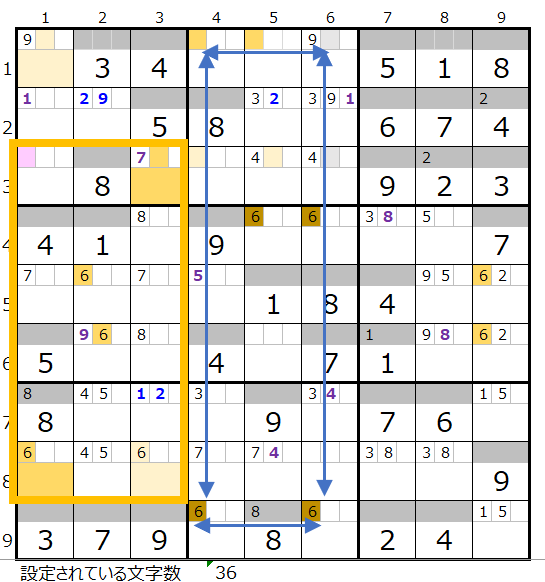
左図第1ブロックと第7ブロックにある背景色「濃い」「薄い」のそれぞれ2か所が色分けが同じで共通して通過するマス目になります。
ちなみに、数字「9」を解いて確認すると、この背景色「濃い」「薄い」のいづれにも正解が含まれていない事が解ります。
数字「7」と「6」の特異点
複数連鎖となった場合に考えられる仮説としては、『それぞれの連鎖で色分けも含めて共通するマス目があれば「濃い」「薄い」どちらかに正解のルートが含まれるのではないか?』というものです。
それが今回の問題の数字「7」と「6」のように、複数の連鎖で色分けも同じ共通して通過するマス目がありながら数字「7」は共通するマス目の「濃い」「薄い」どちらかに正解があるのに対して、数字「6」では存在していないとなると、仮設が成立しない事になります。
なおこの2つの共通するマス目をよく見ると次のような特異点があることが解ります。
- 共通して通過するマス目の中にスクウェアになり得る箇所が存在する。
つまり上記の2点が成立する場合は、その数字から正解になるマス目の情報を得ることができない事が確定しますので、その数字はあきらめて別の数字を探る事になります。
ところで『上記以外で複数の連鎖で色分けも同じ共通して通過するマス目の「濃い」「薄い」どちらにも正解がないケースは無いのか?』というご質問に対しては「解っている範囲では上記以外には存在していません」という答え方になりますことをご容赦ください。
複数連鎖の対処法
まずはこの対処法の前置きを記載いたします。
- どうしても複数連鎖しか存在しないような問題があった場合の対処法になります。
- 他に連鎖がユニークになる数字が存在する場合はそちらを優先すべき認識です。
- この対処法は経験則によるものです。
最後に数字「3」の場合を確認して見ます。
④数字「3」で連鎖を考える
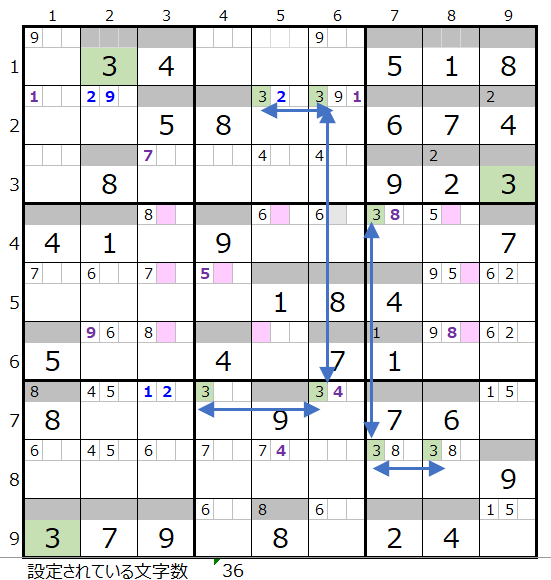
数字「3」は残り6ブロックですが、第2、第8、第9ブロックは2ヶ所確定なので、残りの3ブロックをどのように通るか?になります。
なお6列目は2ヶ所確定しているので第5ブロックの背景色薄灰色のメモ欄には数字は入りません。
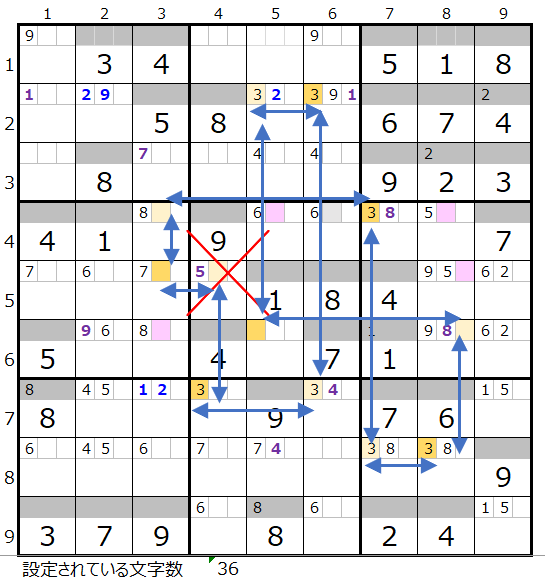
左図のような色分けも正しい連鎖がひとつ考えられます。
今回の問題のように数字が入る可能性のある場所が密集していると気づき難いのですが、赤×印のところは対角を通過するルートの存在が疑われます。
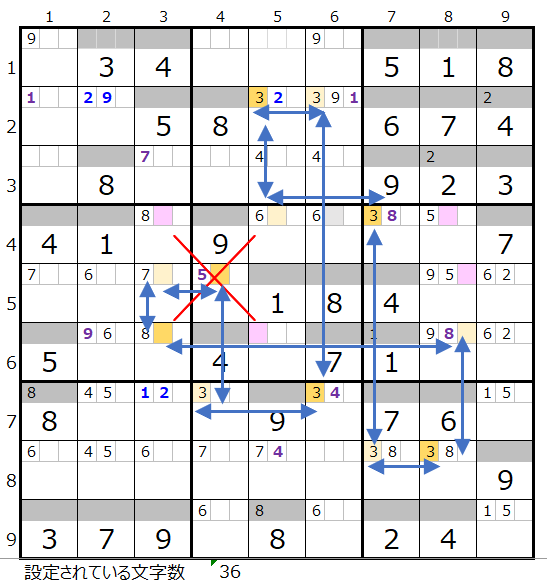
やはりもう一つの連鎖がありました。
ただしこれ以上は無い認識です。
つぎに色分けが同じで両者共通して通過するマス目を確認します。
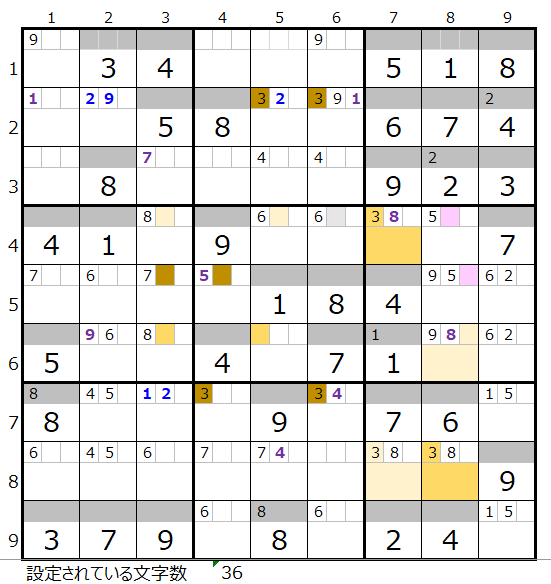
「濃い」「薄い」2か所づつあることが解ります。
この場合は除外しなければならない条件には当てはまりません。
「濃い」「薄い」で数字「3」を仮置きして解き進める事にします。
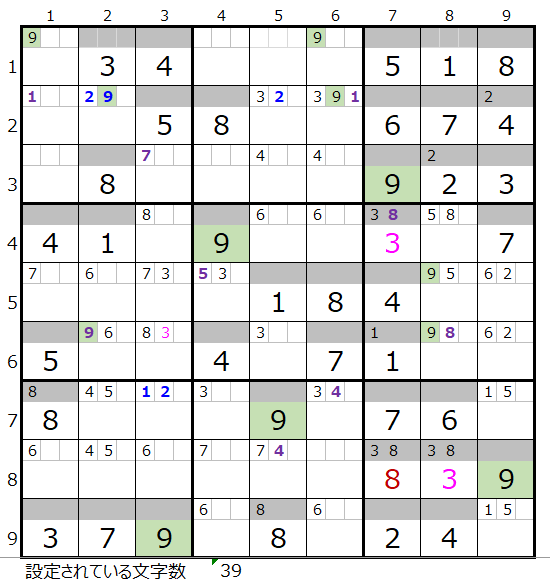
「濃い」場合ですが、すぐに行き詰った状態になります。
更に進めるには、例えば数字「9」の色分けの手法などを使う事が考えられますが、一旦ここまでとして先に「薄い」場合を確認して見る事にします。
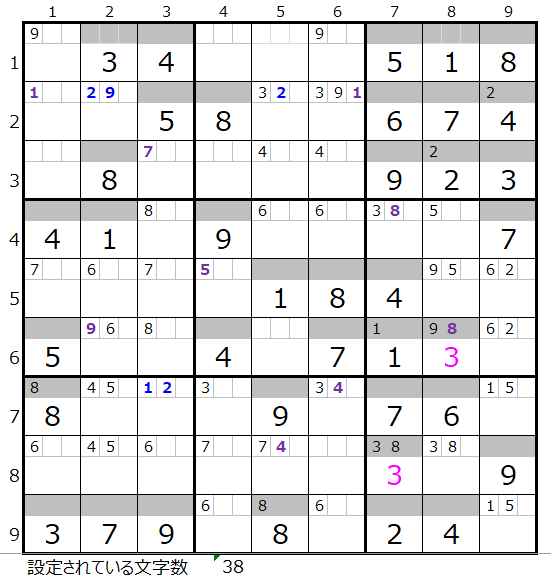
大変恐縮ですが、この盤面につきましては皆様で解き進めていただければ幸いです。
まとめ
すべての数独問題を調べた訳ではありませんので断定はできませんが、その場合でも1から9まですべての数字が「複数連鎖に対応できないパターン」ということは無いような気がします。
複数連鎖さえ探し出せればこちらの対処法の方が解り易いと思われるかもしれませんが、この対処法は二択分岐が必須となるため、問題を解く時のワクワク感が薄くなることは否めません。
次回は本シリーズの最終回として色分けの手法を第1回の時にご紹介した「世界一難しい数独」の問題に適用したらどうなるか?についてご説明したく存じます。
以上最後までご一読いただき誠にありがとうございました。
