これまで14回に渡り「解法その1」~「解法その4」そして「色分けの手法」をご説明して来ましたが、第15回からその後4回に渡り最終回として、第1回の時にご紹介した「世界一難しい数独」の問題に「色分けの手法」を使って再度ご説明してきましたが、いよいよ今回の「その5」が本当の最終回となります。
前回までに左図で×印のところをご説明しましたが、今回は最初の数字「5」「濃い」の二択分岐のもう片方の『二回目の数字「5」「薄い」』の場合についてご説明致します。
これによりすべての分岐が調べ終わることになりますので、今回の中に正解につながる盤面が存在していることになります。
今回の説明で使用する数独問題について
第1回の時にもご紹介していますが、今回の問題は2012/7/3日付の「ロケットニュース24」に掲載されている「世界一難しい数独」になります。
二回目の二択分岐その2「薄い」「5」で仮置きをした盤面
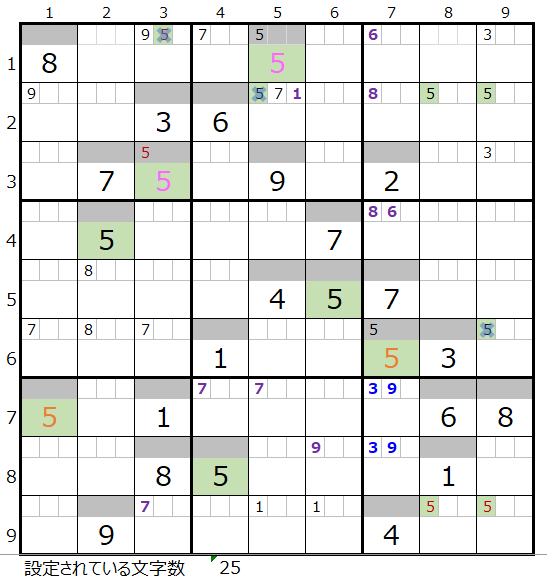
この盤面は第18回「世界一難しい数独その4」からの続きになりますが、文字数は25文字まで来ています。
なお本解法その1から3では盤面として行き詰まった状態です。
左図のメモ欄
・黒字茶字—解法その1からセット
・太紫—解法その2からセット
・太青—解法その3からセット
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれている物を除き)1から9の各数字でメモ欄にその数字が置ける場所の数は次の通りになります。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 18 | 42 | 22 | 30 | 0 | 27 | 9 | 16 | 24 |
数字「7」が9か所でゼロを除いて一番少なくなるので「7」を選択します。
数字「7」で連鎖を考える
複数連鎖をすべて見つけ出すためには、まずは一つ連鎖を見つけて、つぎに対角で置き換え可能なポイントを探して確認し、更に新たに置き換え可能なポイントがあればそれも合わせて確認する、という風にすることで連鎖を漏れなく洗い出することができます。
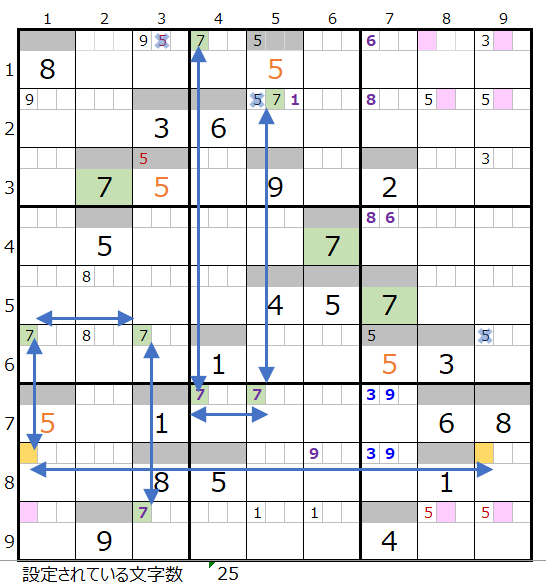
上左図ですが、「解法その1」と「解法その2」の行または列の並びでセットされたメモ線の数字を紺矢印で結んでいます。
8行目の背景色オレンジ色のところは行に2ヶ所しか置く場所がないために必ず通過するポイントであることを表しています。
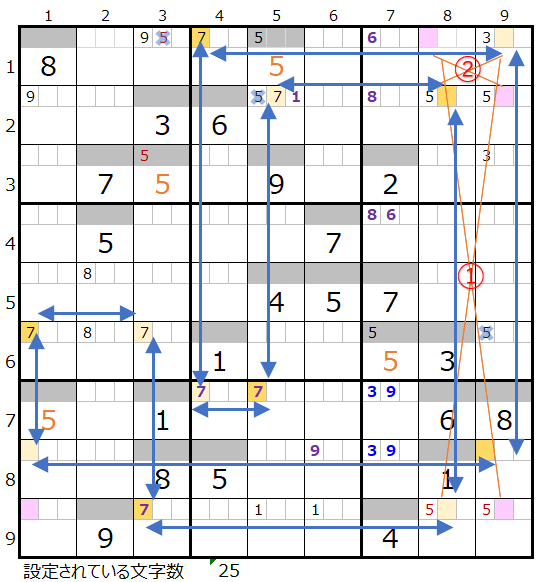
上右図のように色分けが正しい連鎖があることが解ります。
対角で置き換えが可能なポイントは2ヶ所(①と②)あります。

まず①を置き換えてみると上左図のように別ループができるため対象外となります。
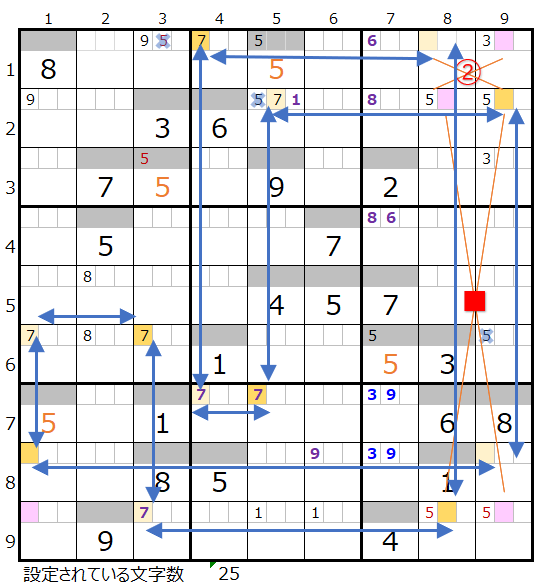
次に②を置き換えると上右図のように色分けが正しいもう一つの連鎖があることが解ります。
なお新たに置き換え可能なポイントとして×■印のポイントが見つかりますが、置き換えると上左図の不成立の連鎖と同じになることが解ります。
以上で成立する連鎖は上記で「成立」した2つになることが解ります。
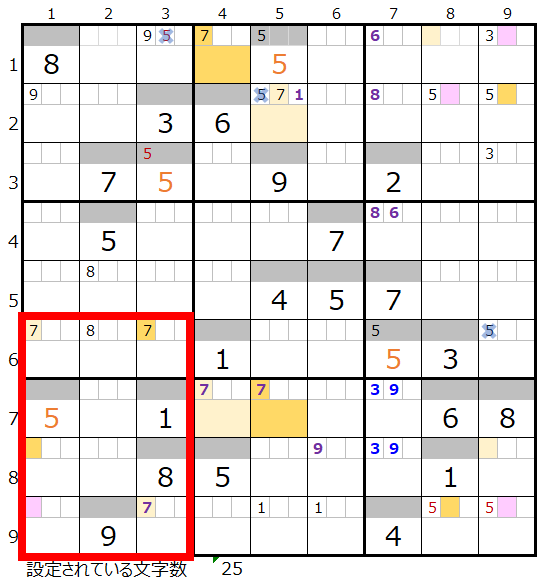
続けて共通して通過するマス目を調べると左図「濃い」「薄い」の背景色を付けたそれぞれ2か所になることが解ります。
これらのマス目の中には「スクウェアになり得る箇所」は存在していませんのでそれぞれの箇所に「7」をセットして二択分岐で解き進めて行きます。
なおお気づきかもしれませんが色分けを入れ替えることで左図赤枠の部分を共通して通過するマス目にすることもできます。
ただしそうなると数字「7」をあきらめることになりますので、それを避けるためにわざと色分けを調整しています。
もしも複数連鎖で「スクウェアになり得る箇所」が含まれる結果になった時は、色分けを調整することで回避できないか?試してみるのも一考です。
「濃い」「薄い」で数字「7」を仮置きした盤面は下記になります。
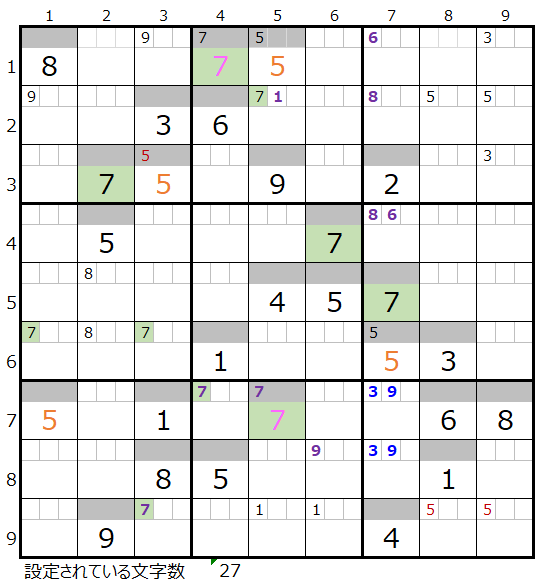
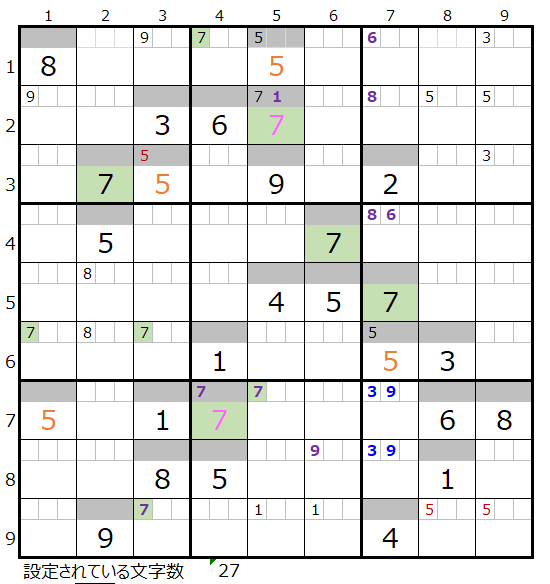
解き進めると、解法その1からその3だけではそれぞれ途中で行き詰まることが解ります。
その盤面は下記になります。
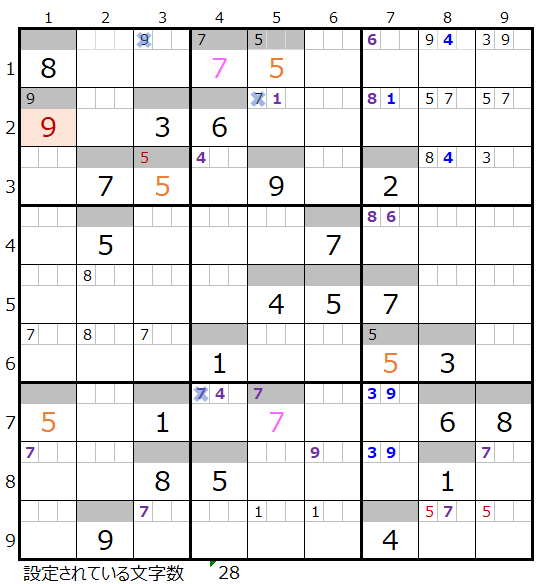
「濃い」方は背景色を付けた「9」が決まります。
なおメモ欄の背景色は省略をしています。
順番が逆になりますが、こちらの「濃い」分岐は後の章でご説明致します。
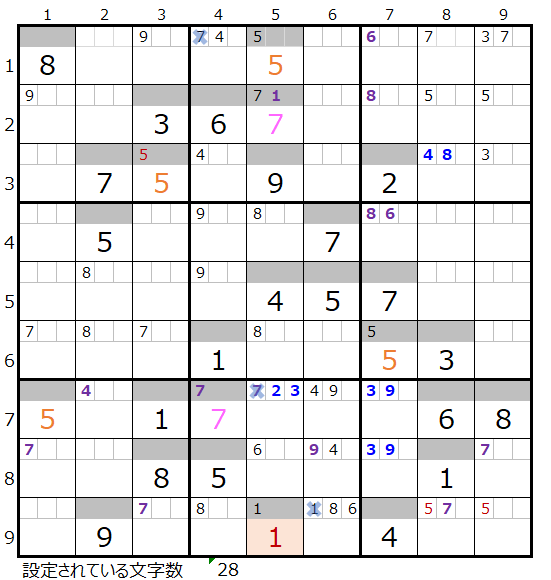
「濃い」方は背景色を付けた「1」が決まります。
なおメモ欄の背景色は省略をしています。
まず先にこちらの「薄い」分岐を次の章でご説明致します。
三回目の二択分岐その1『「薄い」「7」』での盤面
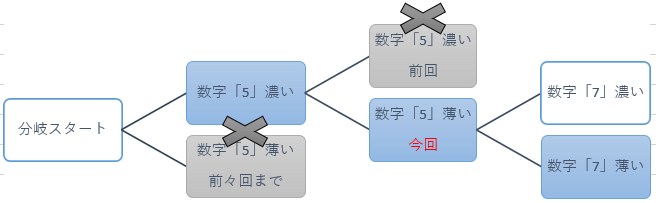
順番が逆になりますが、この章でご説明するのは左図数字「7」「薄い」の場合です。
数字「7」「濃い」につきましては後段でご説明致します。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 18 | 36 | 17 | 20 | 0 | 23 | 2 | 6 | 16 |
数字「7」が数的には一番少ないのですが、既に先ほど二択分岐をしているため、次に少ない数字「8」を選択します。
数字「8」で連鎖を考える
本題に戻って、数字「8」の連鎖について調べて行きます。
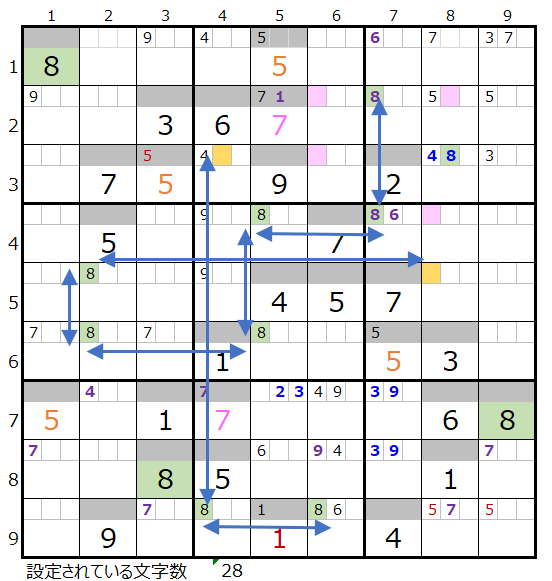
上左図2行目のメモ欄で背景色オレンジ色のところは、その行または列で2ヶ所しか置き場所がないので通過が確定しています。
メモ欄にセットされている情報が多いので連鎖は見つけ易い事と存じます。

上右図のように色分も正しい連鎖がひとつ見つかりました。
なお対角で置き換えが可能なポイントは1ヶ所(①)あることが解ります。
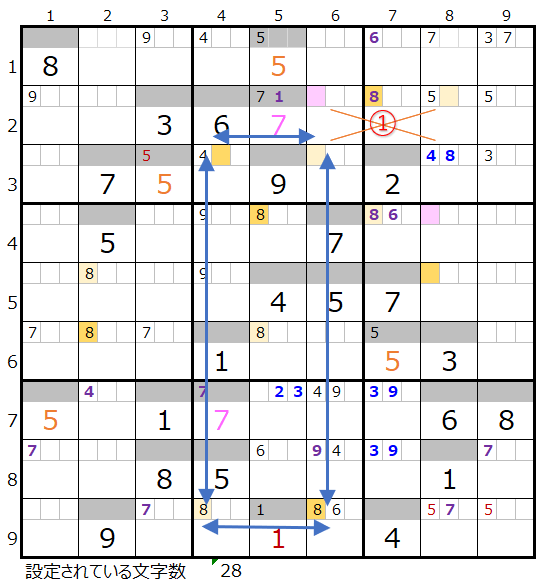
そこで対角で置き換え可能なポイント①を確認して行きます。
ただし①の置き換えは左図紺矢印のところがスクウェアとなるので対象外となります。
となると数字「8」の連鎖は一つしか無く、「色分けの手法」を使って盤面の状況を確認して行きます。
なお残り6ブロックありますので「仮置きしたマス目以外は解けない」個数の判定は有効です。
それでは連鎖の各マス目に1ヶ所づつ数字「8」をセットした場合に「どこまで解けるか?」を確認して行きます。
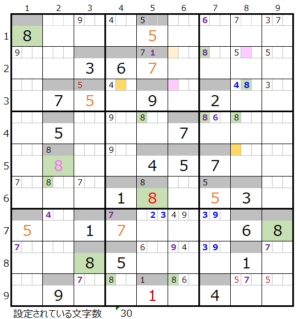
①第4ブロック→第5ブロック
カウントは無し
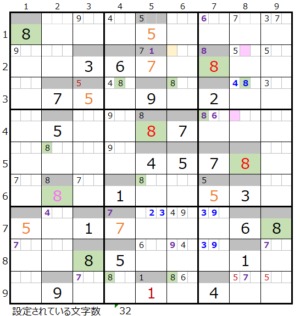
②第4ブロック→第5ブロック→第6ブロック→第3ブロック
カウントは「濃い」2/3
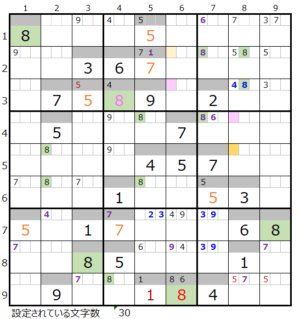
③第2ブロック→第8ブロック
カウントは無し
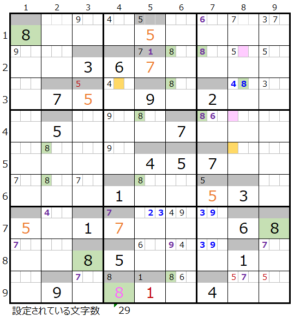
④第8ブロック
カウントは無し(薄い)

⑤第5ブロック→第4ブロック→第6ブロック→第3ブロック
カウントは「濃い」2/3
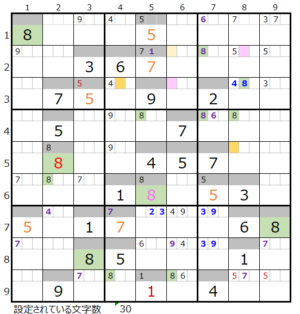
⑥第5ブロック→第4ブロック
カウントは無し
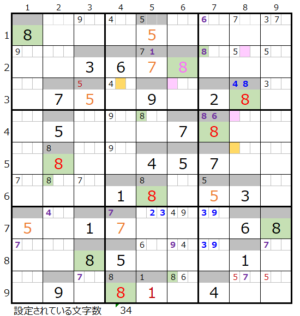
⑦第2ブロック→第3ブロック→第6ブロック→第5ブロック→第4ブロック→第8ブロック
カウントは「薄い」1

⑧第8ブロック→第2ブロック
カウントは無し
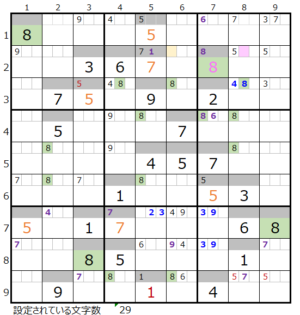
⑨第3ブロック
カウントは無し(薄い)
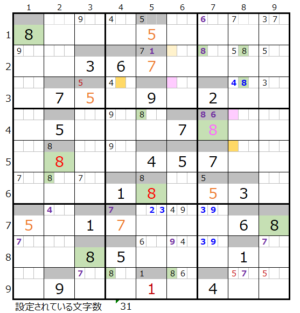
⑩第6ブロック→第5ブロック→第4ブロック
カウントは「薄い」1/2
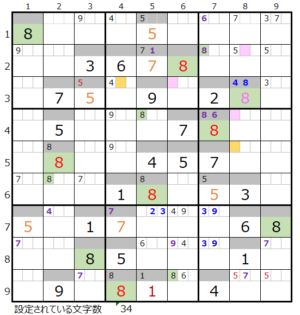
⑪第3ブロック→第6ブロック→第4ブロック→第3ブロック→第2ブロック→第8ブロック
カウントは「薄い」1

⑫第6ブロック→第4ブロック→第5ブロック→第3ブロック
カウントは「濃い」2/3
以上により、カウントの結果としては
・濃い—2/3,2/3,2/3
・薄い—1,1,1/2
となり、「薄い」が「1/2」大きく半分以上の差があり明確な差になります。
なお「 仮置きしたマス目以外は解けない 」個数は
・濃い—1ヶ所
・薄い—1ヶ所
の同数となります。
この結果から「薄い」1/2の盤面を使って解き進めることになります。
「薄い」1/2で仮置きした盤面は下左図になります。
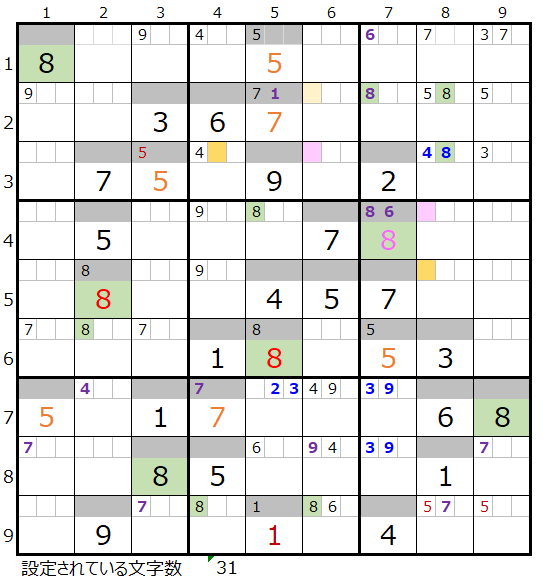
この盤面から解き進めて行きますが、結果は右図になります。なお「どこで行き詰まるか?」はいろいろなバリエーションがあることと存じます。
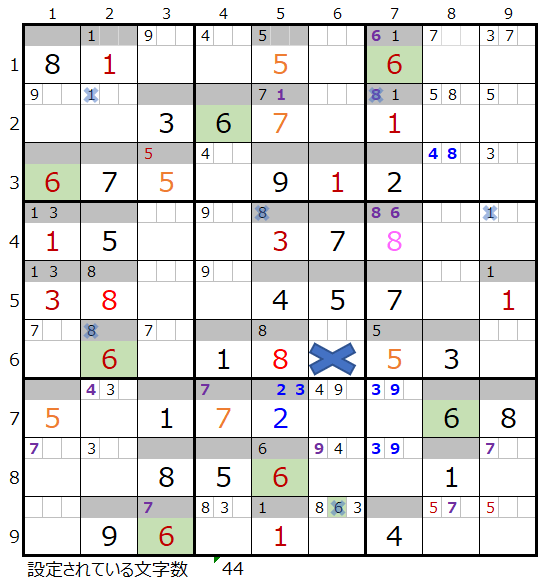
上右図では第5ブロックに数字「8」が入らない事が解ります。残念ながら途中で手詰まり(解けない)という結果になります。
以上の結果から、『三回目の二択分岐その1「薄い」「7」』の分岐には正解が無い事が解りました。
続けて、残っているもう片方の『三回目の二択分岐その1「濃い」「7」』を調べて行きます。
三回目の二択分岐その1『「濃い」「7」』での盤面
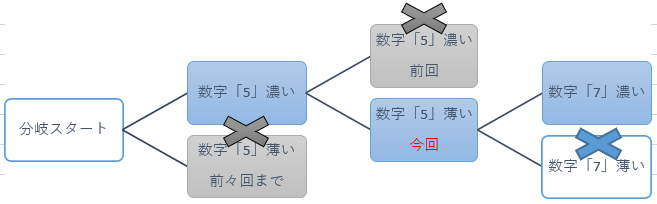
『数字「7」薄い』には正解が無い事が解りましたので、三回目のもう片方の二択分岐その2『数字「7」濃い』方を見て行きます。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 16 | 39 | 20 | 24 | 0 | 27 | 2 | 14 | 13 |
数字「7」が数的には一番少ないことが解ります。一般的には既に先ほど数字「7」で二択分岐をしているため、続けて「7」を選択することははばかられると思われるのですが、数字「7」はまだ残り4ブロックあり、また今回の盤面がとても特徴がある形をしているので数字「7」を選択することにします。
数字「7」で連鎖を考える
何が「特徴がある形」か?と謂うと残り4ブロックが2ブロックづつスクウェアになり得る形での連鎖になっている点です。
これに対して「色分けの手法」を適用した時に「どのような結果になるのか?」についてご説明したく存じます。
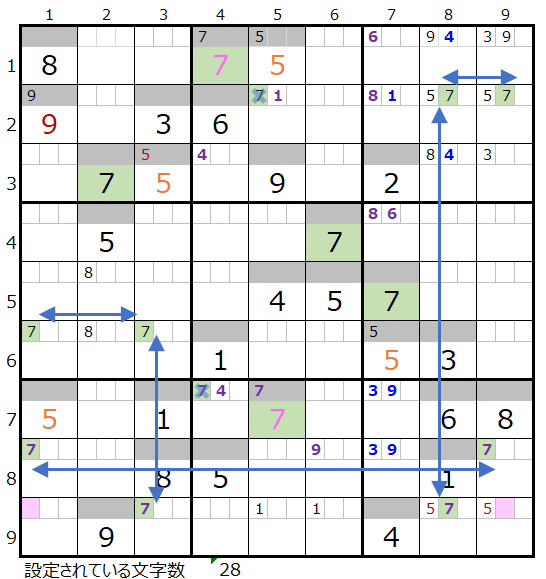
残れ2ヶ所であり、メモ欄にセットされている情報もあるので連鎖は見つけ易い事と存じます。
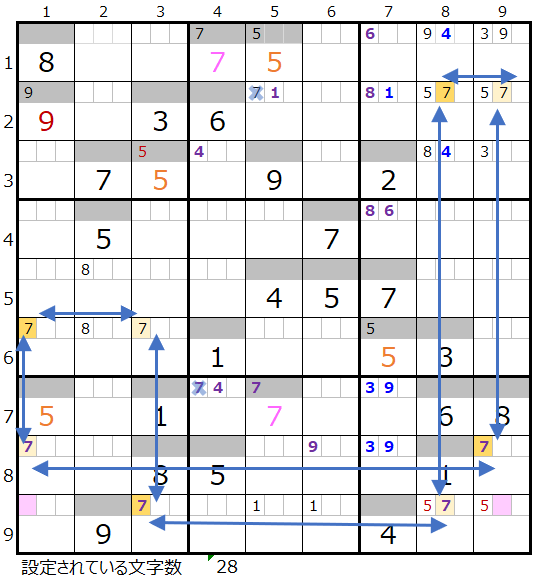
上右図のような色分けの正しい連鎖が見つかります。
先ほど特徴をご説明しましたが、2つのスクウェアになり得るところがあります。
対角に置き換えできるポイントは存在しないので連鎖はユニークである事が確定しますので「色分けの手法」を使って状況を確認をして行きます。

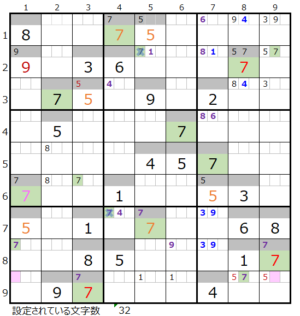
①第4ブロック→第7ブロック→第9ブロック→第3ブロック
カウントは「濃い」1

②第7ブロック→第4ブロック
カウントは「薄い」1/2
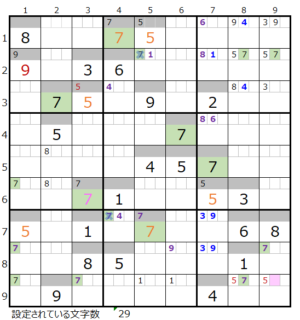
③第4ブロック
カウントは無し
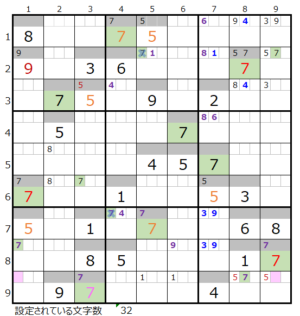
④第7ブロック→第4ブロック→第9ブロック→第3ブロック
カウントは「濃い」1
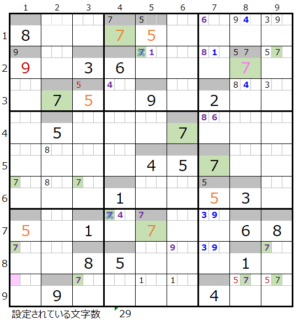
⑤第3ブロック
カウントは無し
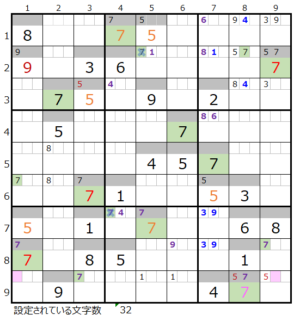
⑥第9ブロック→第3ブロック→第7ブロック→第4ブロック
カウントは「薄い」1
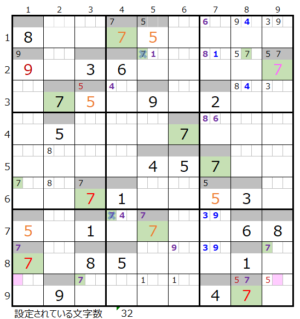
⑦第3ブロック→第9ブロック→第7ブロック→第4ブロック
カウントは「薄い」1
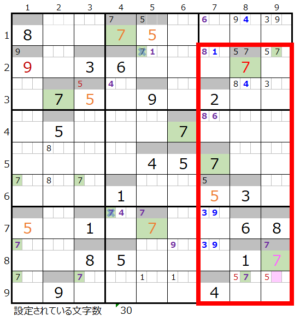
⑧第9ブロック→第3ブロック
カウントは「濃い」1/2
以上により、カウントの結果としては
・濃い—1,1,1/2
・薄い—1,1,1/2
となり、「濃い」「薄い」が同数となり残念ながら両方とも確認する必要があります。
なお上図②の赤枠のスクウェアになり得るポイントは⑧の「濃い」1/2でカバーされ、逆に⑧の赤枠は②の「薄い」1/2でカバーされることになるので、「特徴がある形」であってもスクウェアの対角に正解が潜む危険性は無い事が解ります。
下図のように「濃い」1/2、「薄い」1/2で仮置きをして解き進めて行きます。
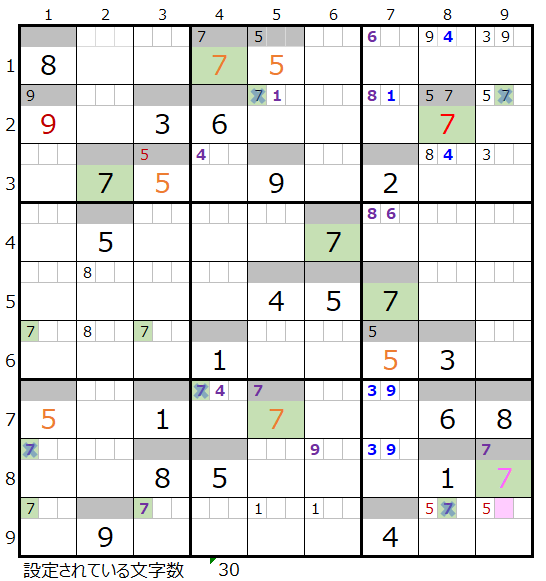
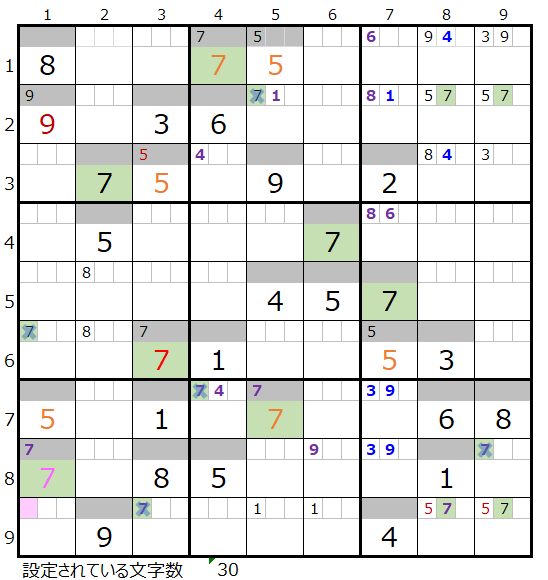
両者を解き進めるとそれぞれ下記盤面になります。
残念ながら「薄い」は途中で手詰まり(解けない)という結果になります。
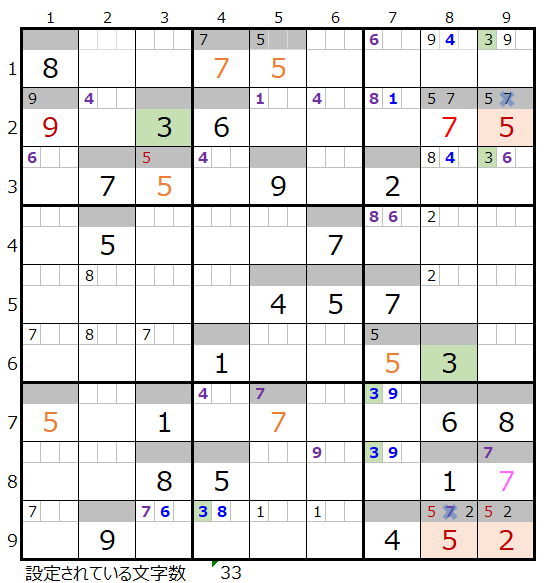
「濃い」方は解法その1から3では上右図まで解き進める事ができますが、これ以上は解き進めることができません。
・背景色の付いているマス目が解決したところです。
・なおメモ欄につきましては背景色は省略しています。
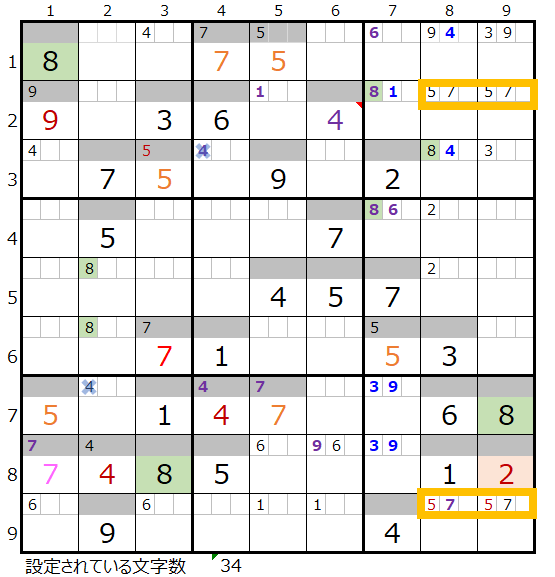
「薄い」方は黄枠のメモ欄にセットされている数字をご確認いただきたいのですが、このスクウェアの配置ですべて同じ「5と7」になっています。
ただこのような状況は数独的にはあり得ない形です。というのもこの場合「5」と「7」の入れ替えが可能となり正解が2つ存在することなってしまうからです。
以上の結果から「薄い」はこれ以上解いても無駄なので不正解となります。
次の章からは残っている「濃い」方を解き進めて行きます。
四回目の二択分岐『「濃い」「7」』での盤面

『数字「7」薄い』は手詰まりになる事が解りましたので、四回目の二択分岐として『数字「7」濃い』方を見て行きます。
メモ欄で該当する数字が置ける場所を確認する
画面は省略いたしますが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 15 | 26 | 19 | 20 | 0 | 24 | 0 | 13 | 13 |
ゼロを除くと数字「8」と「9」がともに数が一番少ないことが解ります。
以下順番に盤面を見て行く事にします。
①数字「9」で連鎖を考える
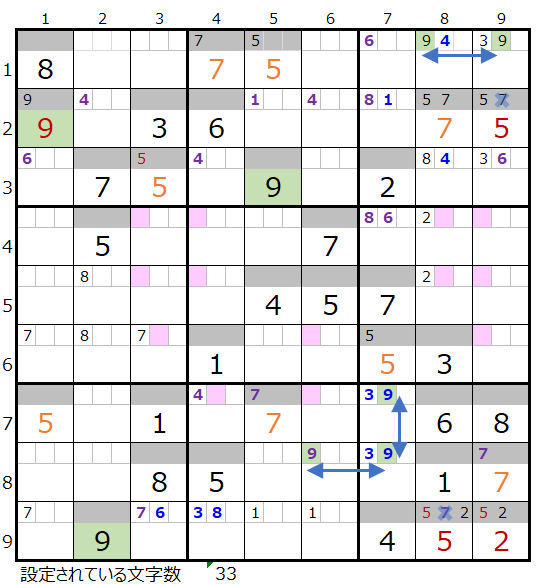
上左図メモ欄の背景色薄ピンク色のところが、既にセットされれている以外で数字「9」を置くことが可能な場所になります。
連鎖としては第5ブロックを中心としてむ右・左・下の3方向につなげることになります。
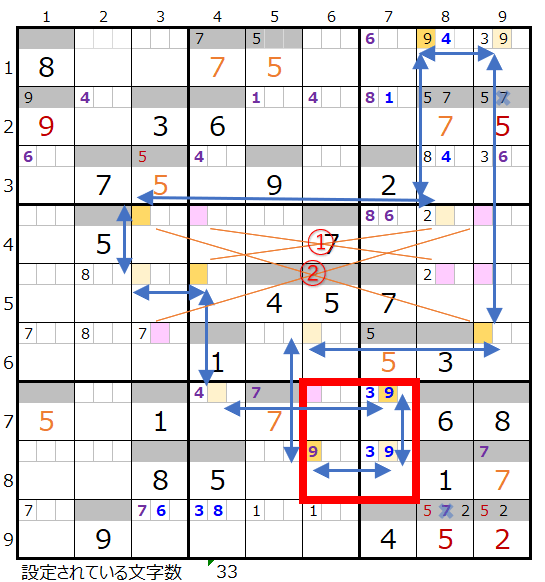
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換えが可能なポイントは2ヶ所(①と②)ありますが、置き換えの対象とならない場所にある赤枠のところはスクウェアになり得る箇所になるので、数字「9」を選択するのは難しそうです。
数字「9」の状況はあまりかんばしくないようなので、次に数字「8」を確認する事にします。
②数字「8」で連鎖を考える

上左図数字「8」は情報が少なく連鎖を考えるのは大変ですが、第2・第3・第6ブロックをどのように通過するか?を考えることになります。

上右図のような色分けの正しい連鎖が見つかります。
対角に置き換えが可能なポイントは3ヶ所(①、②、③)あり、中央に固まっているので共通して通過するマス目が複数残るのは難しそうです。
このように見て見ると、数字「9」も「8」も状況はかんばしくありません。
本来であれば深追いせずに、残り2ブロックある数字「7」での二択分岐に切り替えた方が良いところなのですが、残す分岐もこれだけになっているので、もう少し別な数字を見て行く事にします。
数字「8」「9」に続いて数が少ないのは、数字「1」の15ヶ所、数字「3」の19ヶ所、数字「4」の20ヶ所となっていますので順番に見て行きます。
③数字「1」で連鎖を考える
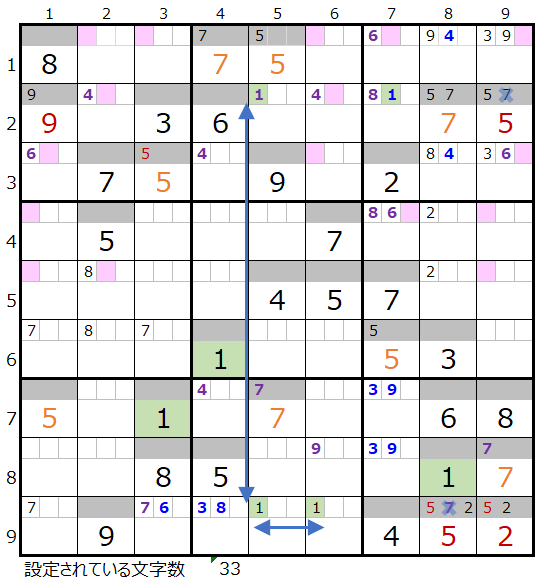
上左図メモ欄の情報が少ないのですが、第4ブロックと第6ブロックは縦方向に2ヶ所で通過する形を考えると見つけ易いかと存じます。
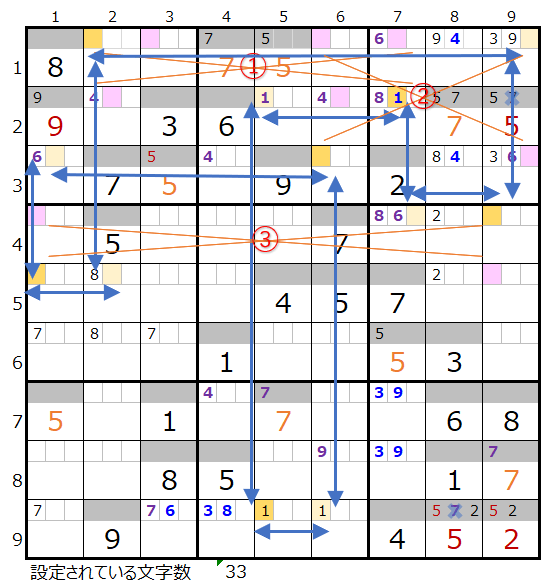
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換えが可能なポイントは3ヶ所(①、②、③)あり、スクウェアになり得る箇所は無さそうですが、全体的に入れ替え可能なポイントがあるので、数字「1」を選択するのは難しそうです。
数字「1」の状況もあまりかんばしくないようなので、次に数の少ない数字「3」19ヶ所を確認する事にします。
④数字「3」で連鎖を考える
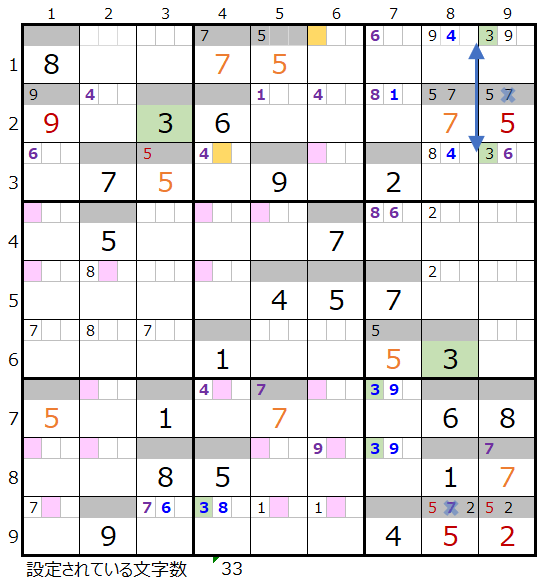
上左図メモ欄の背景色オレンジ色のところは、横方向で必ず通過するマス目になります。
3行目のところはスクウェアになることを避けるとそうなる事になりますが、逆に言うと「スクウェアになり得る箇所」となります。
連鎖としては第8ブロックを中心としてむ右・左・上の3方向につなげることになります。
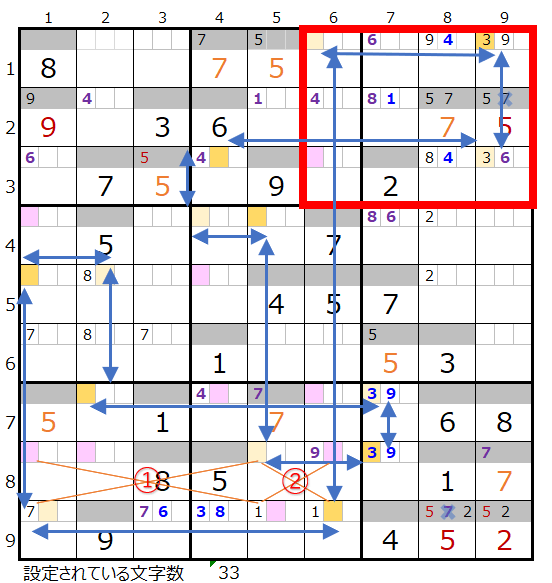
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換えが可能なポイントは2ヶ所(①と②)ありますが、置き換えの対象とならない場所にある赤枠のところはスクウェアになり得る箇所になるので、あまり良さそうではありません。
念のため①の対角での置き換えを調べて見ます。
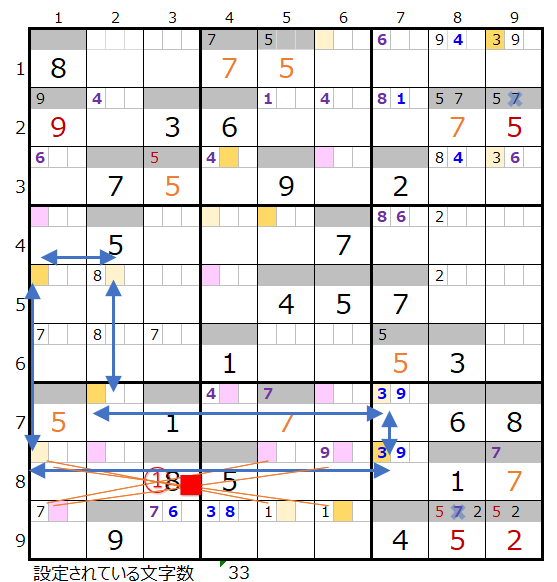
上左図は①の対角での置き換えをした盤面になりますが、連鎖は不成立なのですが、新たに置き換え可能なポイント×■印が見つかります。
この■を置き換えた盤面が上右図になります。
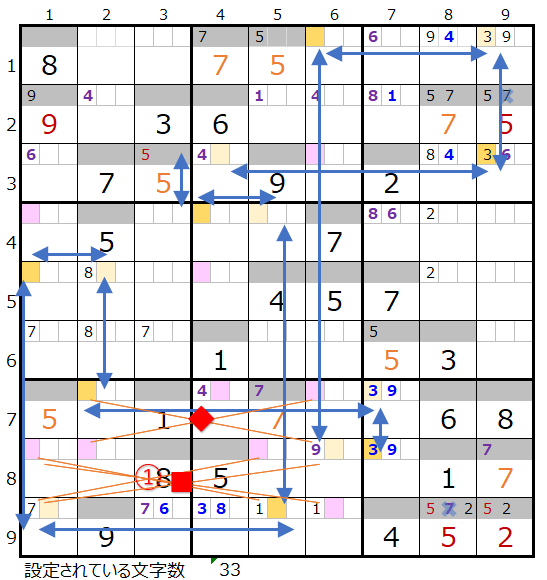
これは成立します。
その上更に置き換え可能なポイント×◆印が見つかります。
実はこれの置き換えも成立するため、更に進めても有効な結果を得るのは難しそうです。
以上の結果から最後に数字「4」20ヶ所を確認する事にします。
数字「4」で連鎖を考える
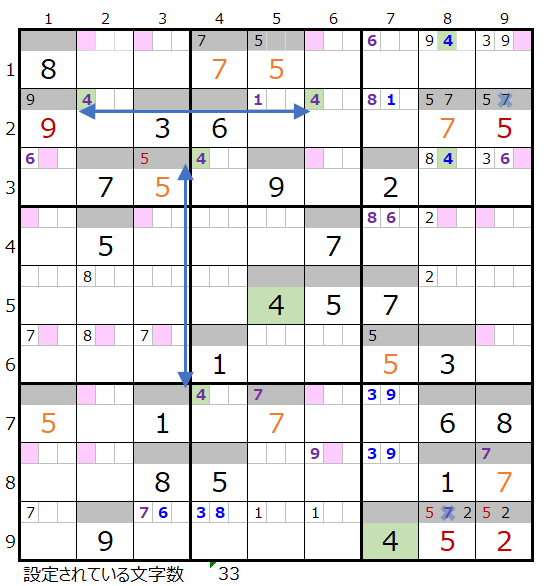
上左図を見ると薄ピンク色のところが多く感じられてどこから手を付けたら良いか?解りづらいかもしれませんが、第2と第8ブロック、第4と第6ブロックをつなげるように考えるとルートが見つけ易い事と存じます。
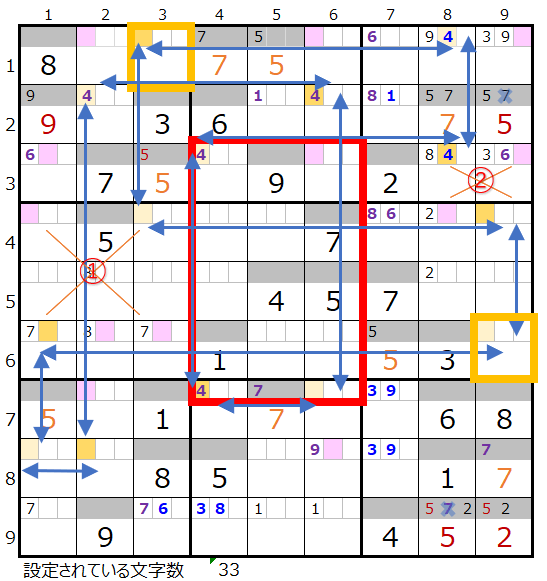
上右図のような色分けの正しい連鎖が見つかります。
対角に置き換えが可能なポイントは2ヶ所(①、②)あり、赤枠のところはスクウェアになり得る箇所になるので、上手くいくのか?不安になりますが①から順番に確認して行きます。
ちなみに黄枠のところは対角で置き換えすることはできませんのでご注意ください。(対角が縦横ともにブロックをまたぐことはできません)
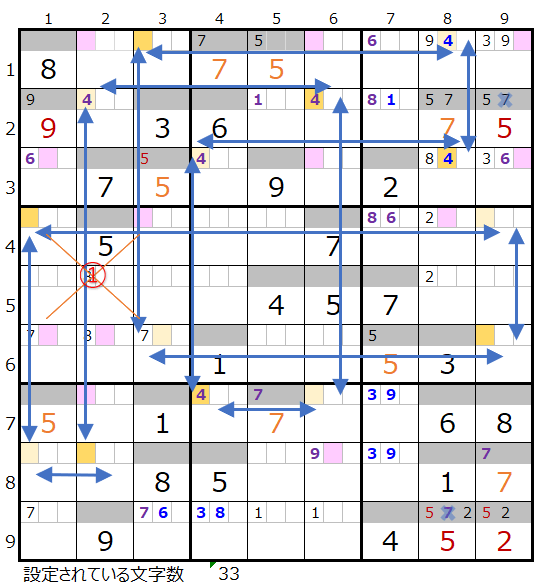
上左図②の置き換えは成立します。
新たに置き換え可能なポイントはありません。

次に②を置き換えた場合ですが、上右図のようにスクウェアができるので対象外となります。
ただし×■印のところに新たな置き換えポイントが現れるので次にこれを置き換えて見ます。
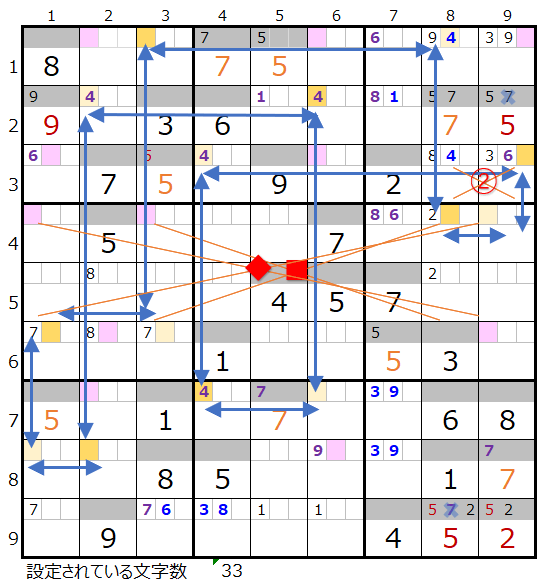
上左図のようにこの置き換えも成立します。
なお新たに置き換え可能な×◆印のところは置き換えると次の上右図と同じになります。
次に①と②を共に置き換えた場合を見て行きます。
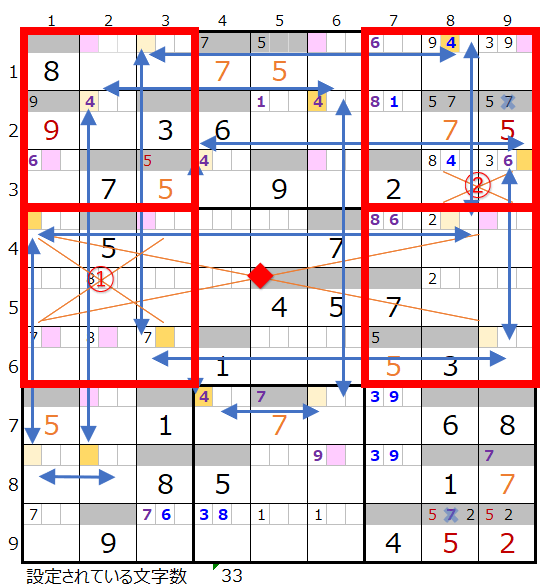
上右図のように①と②同時に置き換え場合は赤枠のブロックで色分けが正しくないため不成立になります。
なお新たに置き換え可能な×◆印のところは置き換えると上左図の盤面と同じになります。
以上の結果から成立する連鎖は3つになることが解ります。
次に3つの連鎖で共通して通過するマス目を調べます。
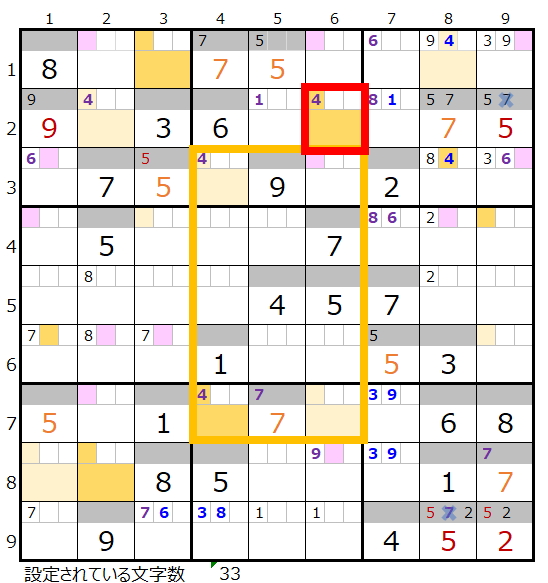
成立する3つの連鎖を共通して通過するマス目を調べると左図で「濃い」「薄い」でそれぞれ背景色を付けたところになります。
経験則としては「共通して通過するマス目の中にスクウェアになり得る箇所が含まれる場合はその数字はあきらめる」としているのですが、今回もおきて破りにはなりますが、黄枠のスクウェアが正解だった場合に影響を受ける赤枠は除外して対応することにします。
従いまして今回は赤枠を除いた「濃い」3ヶ所と「薄い」5ヶ所を採用することにします。
下図のように「濃い」「薄い」それぞれ仮置きをして解き進めて行きます。
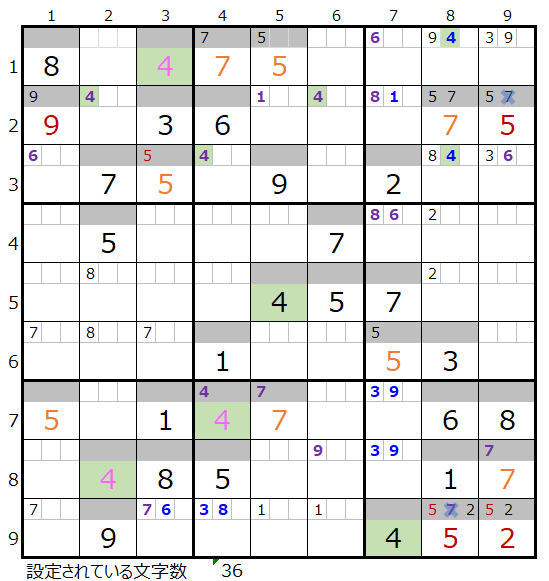

両者を解き進めるとそれぞれ下記盤面になります。
残念ながら「濃い」は途中で手詰まり(解けない)という結果になります。
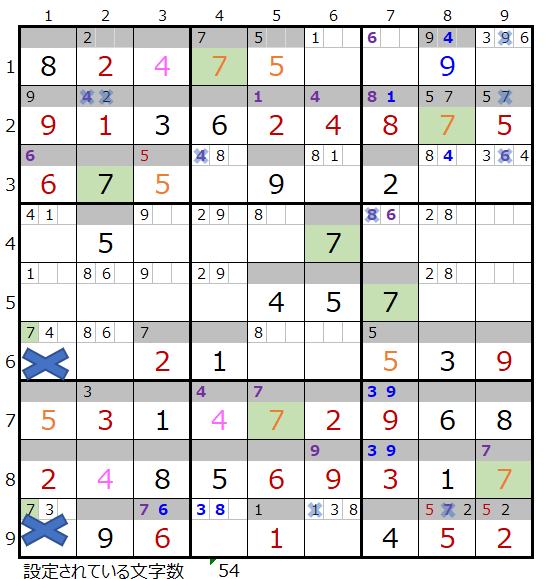
上左図第4ブロックと第7ブロックの×印のマス目にともに「7」が入る事になり、手詰まり(不正解)であることが解ります。

「濃い」方は解法その1から3では上右図まで解き進める事ができますが、これ以上は解き進めることができません。
・マス目が解決したマス目及びメモ欄につきましては背景色を省略しています。
以上の結果から数字「4」「濃い」には正解が無い事が解りました。
次の章からは残っている数字「4」「薄い」の方を解き進めて行きます。
五回目の二択分岐『「薄い」「4」』での盤面
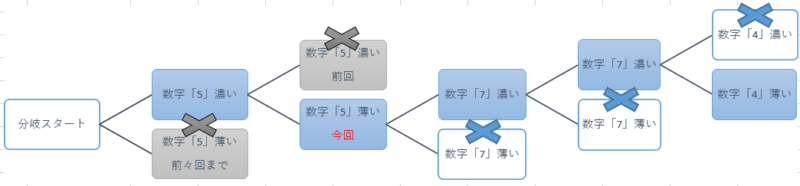
『数字「4」濃い』は手詰まりになる事が解りましたので、五回目の二択分岐としてまだ残っている『数字「4」薄い』方を見て行きます。
メモ欄で該当する数字が置ける場所を確認する
随分と数が少なくなってきましたが、(既に置かれているものは除き)メモ欄に各数字を置ける場所の数は次の通りです。
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数字が置ける場所の数 | 0 | 9 | 7 | 0 | 0 | 12 | 0 | 1 | 3 |
ゼロを除くと数字「8」が一番少ないことが解ります。
数字「8」で連鎖を考える
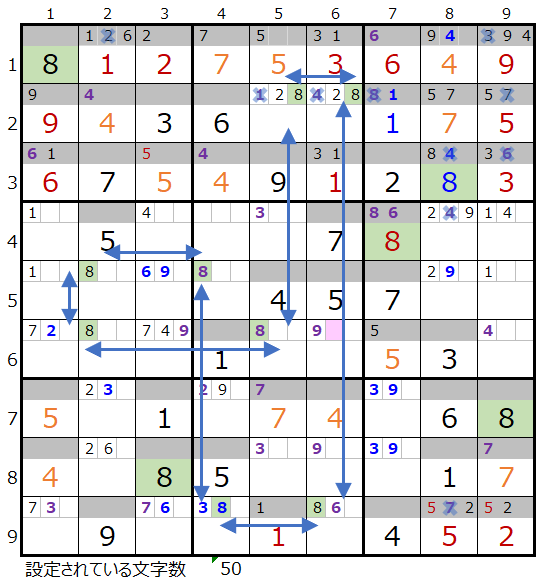
上左図でメモ欄にセットされている情報をもとにつなげ行くと連鎖ができます。
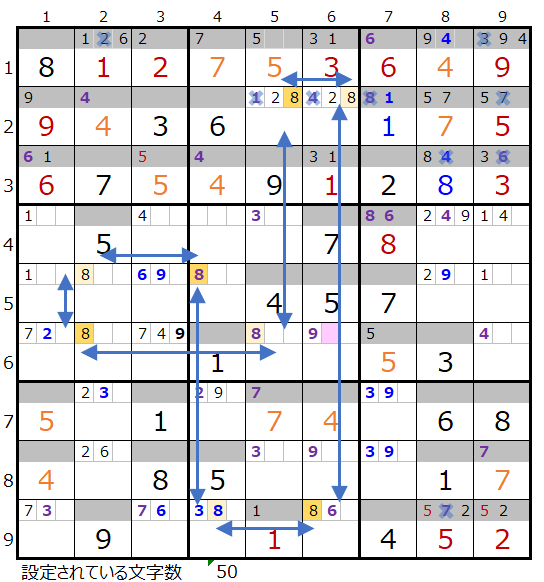
上右図のように色分も正しい連鎖がひとつ見つかりました。
なお対角で置き換えが可能なポイントはありませんので連鎖はユニークになります。
「色分けの手法」を使って状況を確認をして行きます。


①第4ブロック→第8ブロック
※第5ブロックのメモ欄に「8」がセットされることで第8ブロックが決まります。
カウントは「薄い」1/2
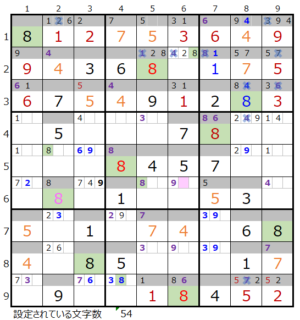
②第4ブロック→第5ブロック→第8ブロック→第2ブロック
カウントは「濃い」1
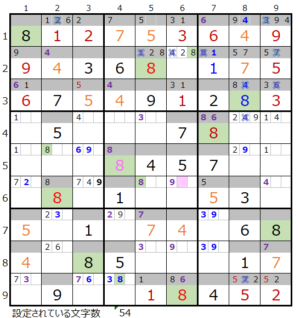
③第5ブロック→第4ブロック→第8ブロック→第2ブロック
カウントは「濃い」1
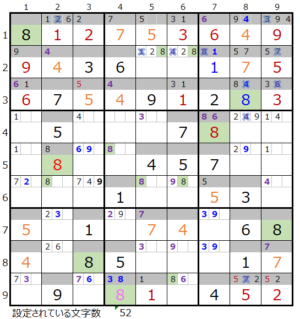
④第8ブロック→第4ブロック
カウントは「薄い」1/2
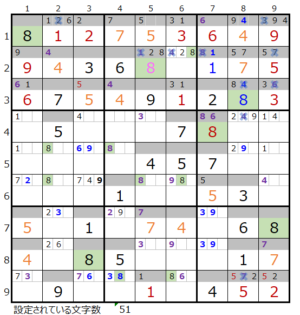
⑤第2ブロック
カウントは無し
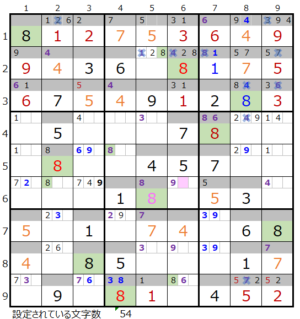
⑥第5ブロック→第4ブロック→第8ブロック→第2ブロック
カウントは「薄い」1
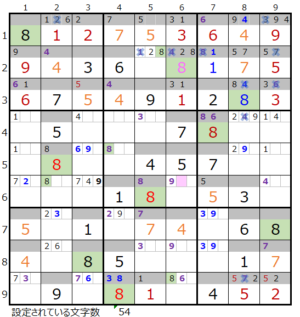
⑦第2ブロック→第8ブロック→第5ブロック→第4ブロック
カウントは「薄い」1
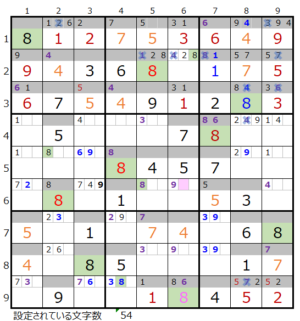
⑧第8ブロック→第2ブロック→第5ブロック→第4ブロック
カウントは「濃い」1
以上により、カウントの結果としては
・濃い—1,1,1
・薄い—1,1,1/2,1/2
となり、「濃い」「薄い」が同数となり残念ながら両方とも確認する必要があります。
下図のように「濃い」1、「薄い」1/2で仮置きをして解き進めて行きます。
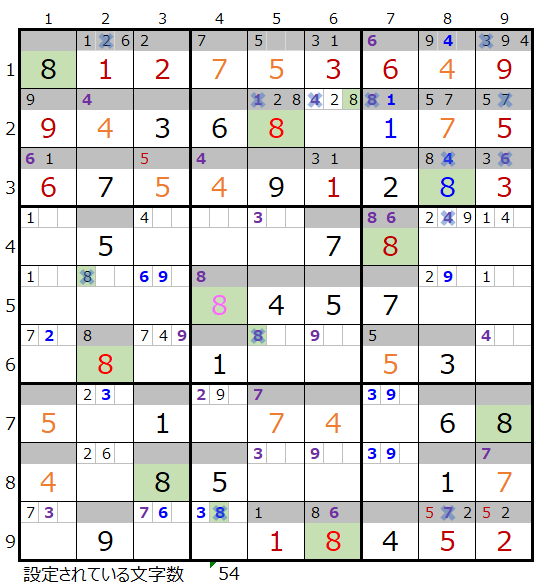
上左図のように数字「8」がすべての埋まった状態からになります。
なお大変恐縮ではございますがこの続きにつきましては皆様でご確認いただければ幸いです。
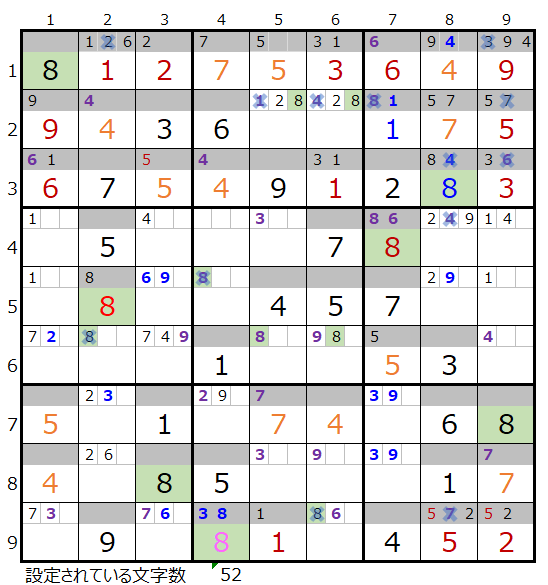
「薄い」の場合は、しばらく解き進めると下図のように手詰まり(不正解)であることが解ります。
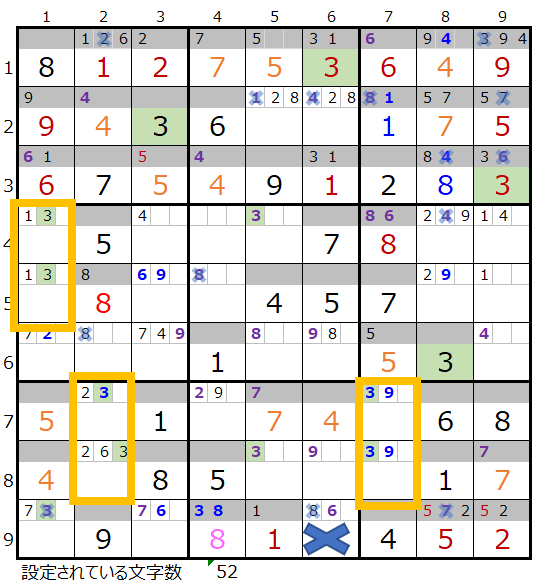
第7と第9ブックの数字「3」のメモ欄の情報から第8ブロックには9行目に数字「3」が入ることになりますが、空いている×印のマス目の列には既に数字「3」が存在するために手詰まりとなります。
まとめ
今回までに5回に渡り「世界一難しい数独」を「色分けの手法」を使用して解いてきました。
当初は「複数連鎖でスクウェアになり得る箇所がある時はその数字はあきらめる」想定でいましたが、いざ「世界一難しい数独」を解くとなると複数連鎖が当たり前のように現れる事になると、そうは言っていられない状況となり「おきて破りの対処法」を何度か使用しなければならない状況に陥ってしまいました。
そもそも「色分けの手法」は経験則にもとづく手法のため、ロジカルに解くという形にはなっていないので、簡単には使えないように思われることと存じます。
また連鎖を漏れなく洗い出すところが後から見なすと結構見落としがある場合があって試行錯誤無しに1回で済むことはほとんどありませんでした。
ということで次回数独の解法を考える際にはロジカルに解ける形で挑戦をしたいと思います。
以上最後までご一読いただき誠にありがとうございました。


