「書式を使用して難しい数独をどのように解くのか? 第1回概説」に記載した3つの解法とプラスαについて、複数回に分けて具体的に説明をしています。
今回は第9回目で「二択分岐による解法」になります。
なお今回で一通りのご説明は終わりとなりますので、一旦シリーズとしては終了いたします。
今回の説明で使用する数独問題について
今回もここ数回と同じく下記サイトの2015年11月の問題集を使用させていただいています。
今回は「数独問題集(達人級)」2015/11/18下段の問題を使い、まだご説明できていないいポイントをお伝えしたく存じます。
手かがりが少なく解くのが難しいと感じられるかもしれませんが、良く考えられた問題になっている認識です。
なお、コピーライトは問題を作られている数独無料問題集様がお持ちのものになりますので初期の盤面につきましては、上記サイトにてご確認いただけますようお願い申し上げます。
「解法その1」終了時の盤面
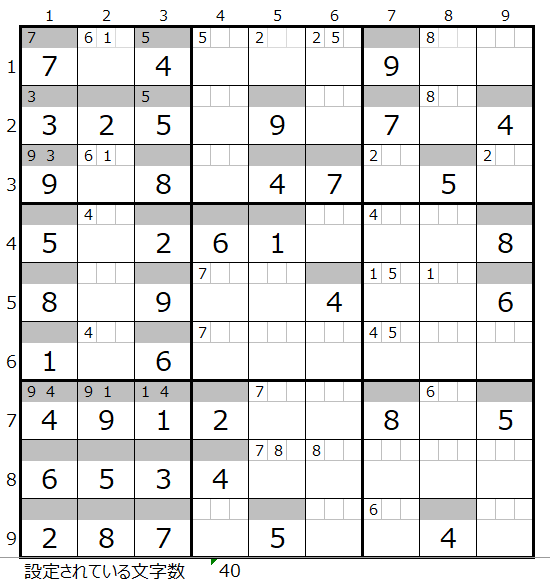
左図は「解法その1」で設定されている文字数40まで解き進んだ状態です。
「解法その1」で得られた情報はメモ欄に記入してあります。
左上のブロックに、2つのマス目に同じ組み合わせの「6,1」のペア数字がある以外は特筆すべきポイントはありません。
「解法その2」終了時の盤面
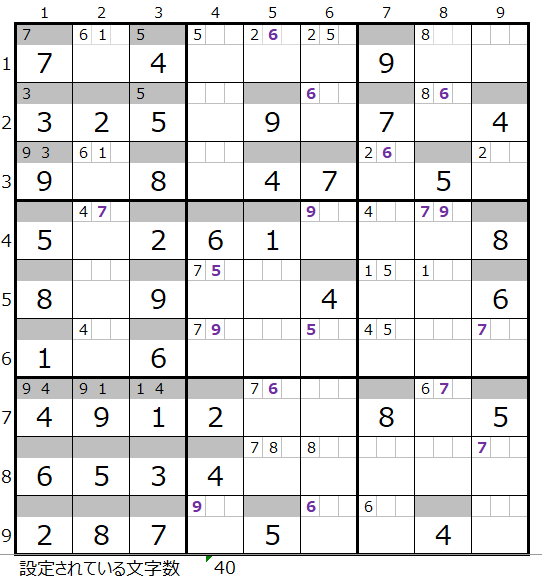
左図のメモ欄で紫色太字の数字が「解法その2」で得られた情報になります。
行方向、列方向で入る可能性が2つのマス目の場合なので、たまたま同一ブロックに同じ数字が入っていたとしても、必ずどちらかに数字が入る訳ではありません。
「解法その2」の情報は「解法その4」に向けた準備情報的な役割になりますので、「解法その1」の情報とは、例えば色を分けるとか、太文字にするとか、後から判別できるように記入しておくと後々便利になります。
「解法その3」終了時の盤面
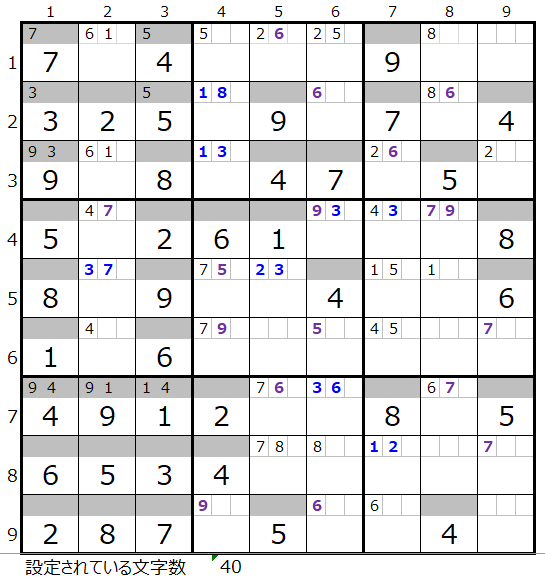
青色太字でメモ欄に記入されている数字が「解法その3」で得られた情報です。
※ちなみに、5行5列のマス目のメモ欄にセットされた「2,3」ですが数字の「7」は解法その1で、このブロックのメモ欄に「7」がセットされているのを使っています。
残念ながら「解法その3」でもマス目の文字を特定するような情報を得る事はできませんでした。
盤面としては行き詰まった状態です。
「解法その4」のためには設定されている文字数やメモ欄の情報が足りない
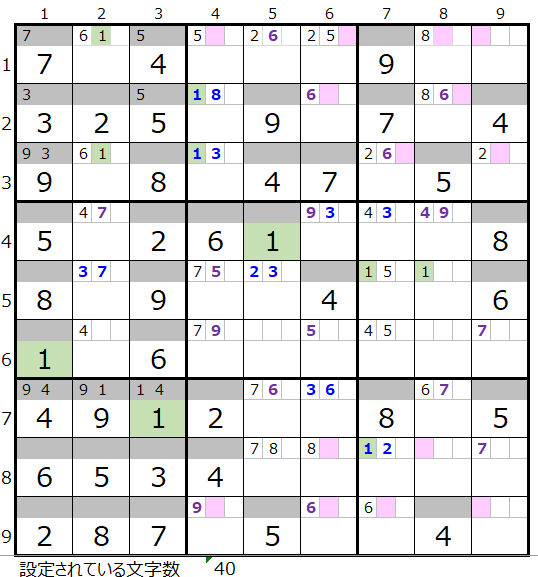
「解法その4」のためには設定されている文字数が40台後半にならないと、一般的には情報が足りない状態になります。
左図は数字の「1」で「解法その4」を試みた場合になります。
背景色薄ピンク色のメモ欄が「1」が入る可能性がある場所になるのですが、選択可能なパターンの数が多いので、絞り込むのは難しい状況です。
最終手段としての二択分岐
このようになると、二択分岐することで無理やり設定されている文字数を増やし局面を打開する方法しか手段を持ち合わせておりません。
今回のような状況では、メモ欄に同じ数字のペアが入っている場所を数えるというやり方は困難です。
二択分岐をする場合、一つの数字はその後の展開が見込めたとしても、もう片方の数字がほぼほぼ進まないとなると、進まない方の数字を状況を確認するために更に二択分岐を繰り返すような事態に陥ってしまいます。
それでも最終的には正解にたどり着くことはできる事と思いますが、できる限り効率的なポイントを選択したいところです。
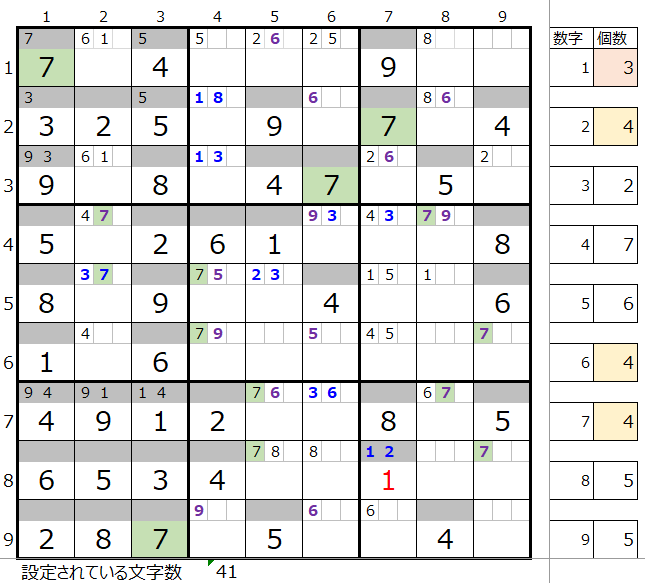
一つのご提案としては、設定されている文字数に対して数字ごとの個数を数えて、その中から多いものと少ないものを除いた数のペアの中から存在するもの選ぶという方法です。
ただし、その際に選択するポイントは50%の確率で正解が存在している必要があります。
正解が含まれない「フェイク」のポイントを選んでしまっては二択分岐をする意味がありません。
- 「解法その3」から得たポイント
- 「解法その3」はその場所に入る可能性のある数字が2つの場合ですので、どちらかは必ず正解になります。
- 「解法その1」から得たポイントの内、
- 同じ行、同じ列、同じブロックにある2つのマス目に同じ2つの数字がペアで入っている場所
- 3つのマス目に3つの数字のペアが入っている場所(少しレアなケース)
上記2つのどちらを選ぶのが良いか?につきましては、ケースバイケースなので、何手か先を確認して展開が望めそうなものを選ぶのが良い認識です。
なお上記「2」の場合は2か所の数字が設定されるので好ましいように思えますが、効果が限定的になる場合もありますので確認した方が間違いがありません。
いずれにせよ、どこを選んで二択分岐をするか?によって、解答にたどり着くまでのルートは数多く存在することになりますので、どれが正しいという事はありませんが、あまり手数を掛けずに解答にたどり着くことができるのが理想的にはなります。
少し解いてみる
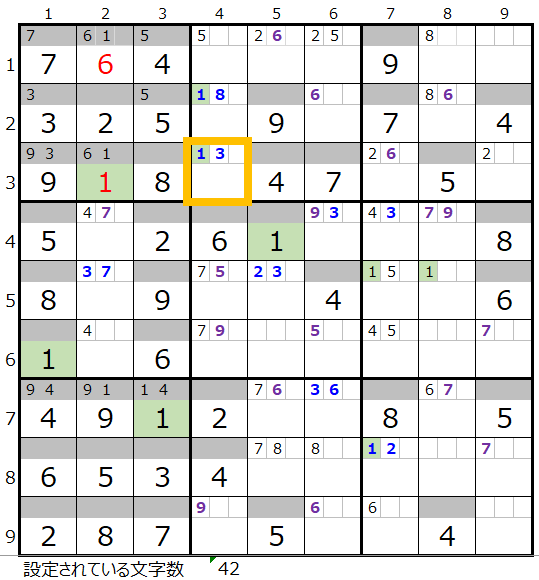
今回は下記の数字の組み合わせを採用することにします。
- 数字の「1」–3回
- 数字の「6」–4回
1行2列に「6」、3行2列に「1」が入ります。
ここで注目していただきたいのが、3行目の黄枠のマス目です。
このメモ欄の「1,3」は「解法その3」でセットされたもので、3行2列に「1」が入ったという事は、黄枠りマス目は数字の「3」に確定します。
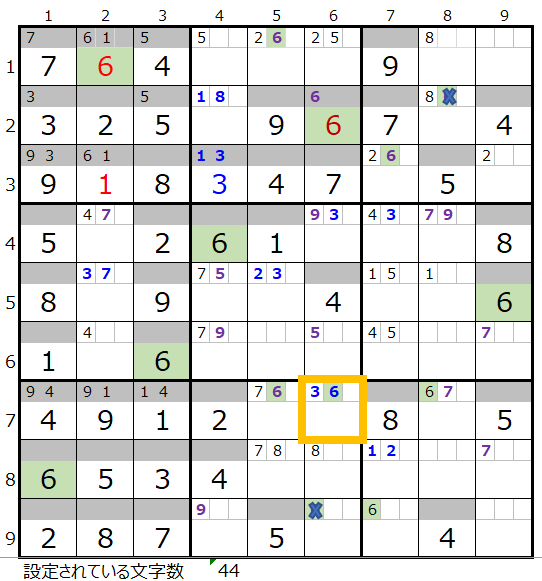
数字の「6」を解き進めて行くと、2行6列に「6」が入ります。
そうすると先ほどと同じような理由から、左図の黄枠には「3」が入る事が確定します。
7行6列に「3」が入ると、6列目を確認していただくと、もう一つ数字が確定するマス目があることが解ります。
ただし、残念ながらこの先「6」を解き進めて行くと「6」を入れられないブロックが出てきて、1行2列が「6」では解けない事が解ります。
まとめ
これまで9回に渡り、書式を使用した数独の解き方についてご説明されていただきました。
「解法その2」「解法その4」で得られた情報は、マス目の数字を確定するよりも、盤面を俯瞰した時に、数字が入る可能性のあるポイントを探るための手法となります。
従いまして、具体的に数字を確定させる時は、あくまでも「解法その1」により確認してから、マス目に数字をセットするようにします。
この事で正答を含まないメモ欄に惑わされずに解き進めることができます。
この後の「数独」に関する記事の予定としては下記の2点になります。
- 第8回のまとめで少し触れた「組み合わせの整合性を確認する事で解法につながるか?」の確認を進める。
- 今回の問題の解法について、解り易い形での説明動画が作成する
以上、最後までご一読いただきありがとうございました。
2019/8/28追記
この記事を書いてからまもなく3ヶ月となりますが、8月ほぼ1ヵ月を掛けて「二択分岐はなるべく使わない形で解けないか?」「その場合にはどのような書式が良いか?」という検証を進めて来ました。
これは上記「まとめ」で記載した「組み合わせの整合性を確認する事で解法につながるか?」を確認するためになります。
検証の進め方としては、「数独問題集(達人級)」2015年11月の問題集にある48問をすべて解く形で実施しました。
(大変申し訳ございませんが、すべての問題を解かずに問題集から記事で利用する問題をピックアップをしておりました…)
その結果としてこの記事で利用させていただいた「2015/11/18下段の問題」は二択分岐を使用しない形で解くことができることが解りました。
つきましては、そのやり方についてこの後数回に渡りご説明をいたしたく存じます。
何卒よろしくお願い申し上げます。

