書式で難しい数独をどのように解くのか?　第6回解法その4-1

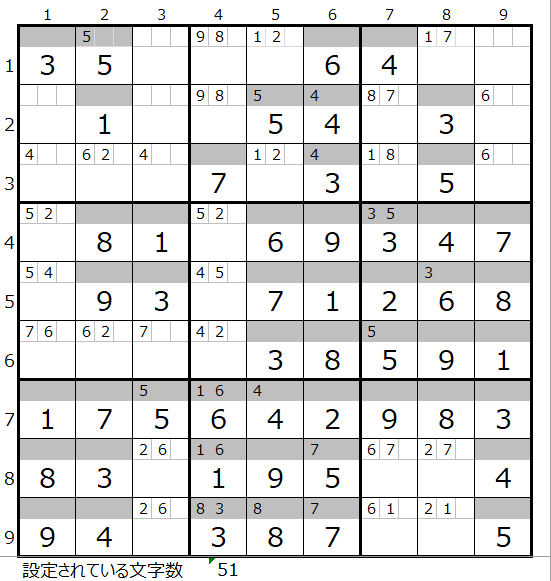
左図は「解法その1」を使って「設定されている文字数」が51になるまで解き進んだ状態になります。

状況としては、「解法その1」ではこれ以上の情報を得ることができません。

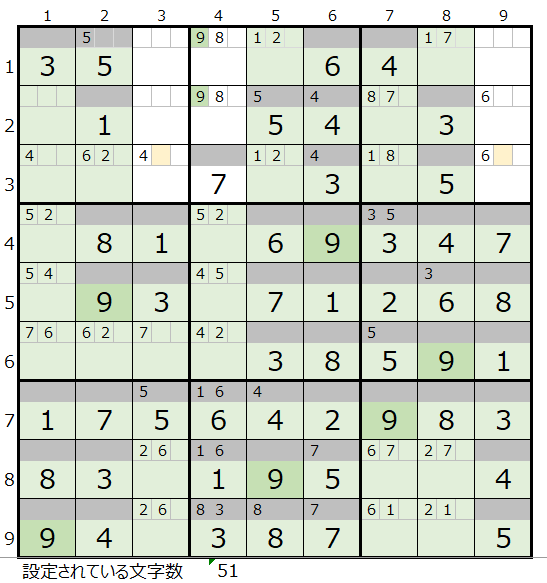
そこで「解法その2」で数字の「9」から確認してみます。

すると3行目の3列と9列の背景色薄ベージュ色のマス目のメモ欄が行方向の候補になることが解ります。

列方向は「解法その1」で既にもとめられているもの以外は存在しません。

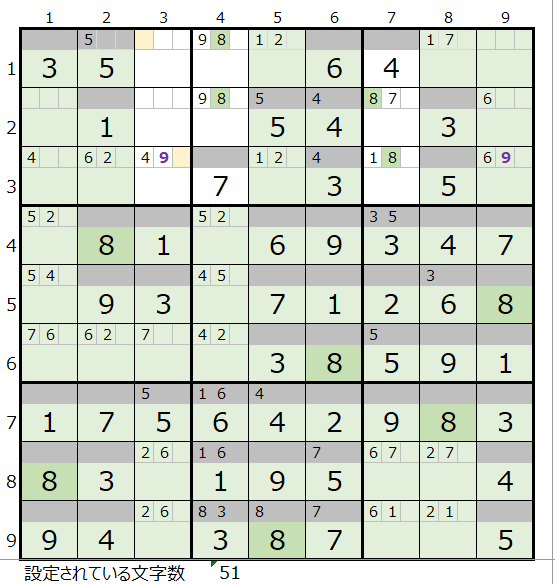
次に数字の「8」を調べて見ます。
すると行方向で、1行目と3行目の背景色薄ベージュ色のマス目のメモ欄が候補になることが解ります。

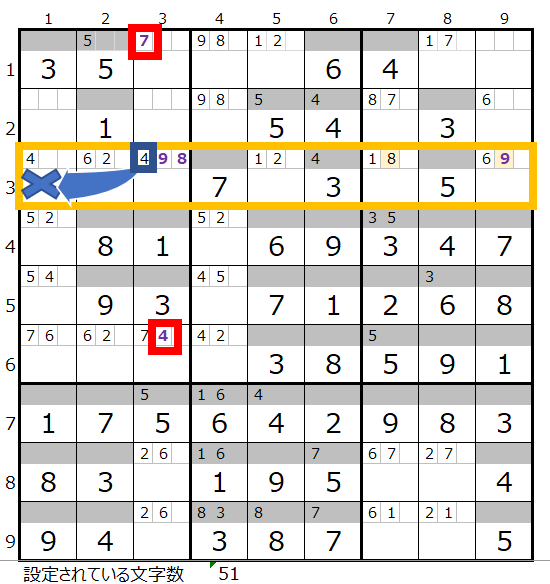
そうなりますと、3行3列のマス目は「解法その1」で埋められた数字の「4」が「3行1列に移動するのでは?」と思われるかもしれませんが、残念ながらそうはなりません。

同じ行の7列目、9列目に数字の「8」と「9」がありますので、3行3列のマス目に「4」が入る可能性を否定できません。

以下同様に数字の「7」から調べて行くと、赤枠の箇所のメモ欄のように「7」と「4」が入ることが解ります。

「解法その2」で解る情報は、ここまでになります。

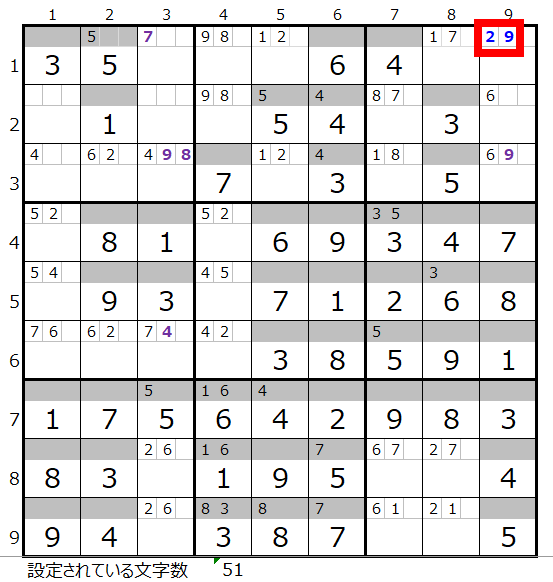
続けて「解法その3」で調べて見ます。

すると左図赤枠のマス目のメモ欄に数字の「2」と「9」が入ることが解ります。

ただし、「解法その3」を使ってもこれ以上情報を得る事はできません。

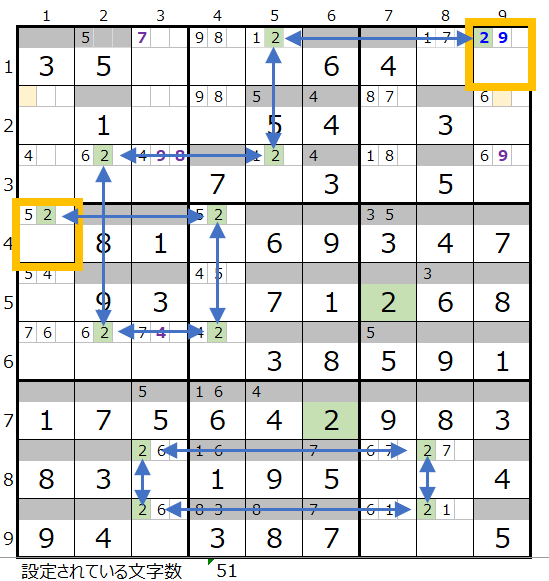
左図は数字の「2」について調べているところです。

矢印をご確認いただけると幸いですが、黄枠のマス目で線が途切れています。

これをつなげるために、横方向、縦方向で数字の「2」が2つになるように配置できる場所を探します。

すると背景色薄ベージュ色の2行1列と2行9列のマス目のメモ欄に「2」が入れば良い事が解ります。

数字の「2」についてはこれで終わりです。

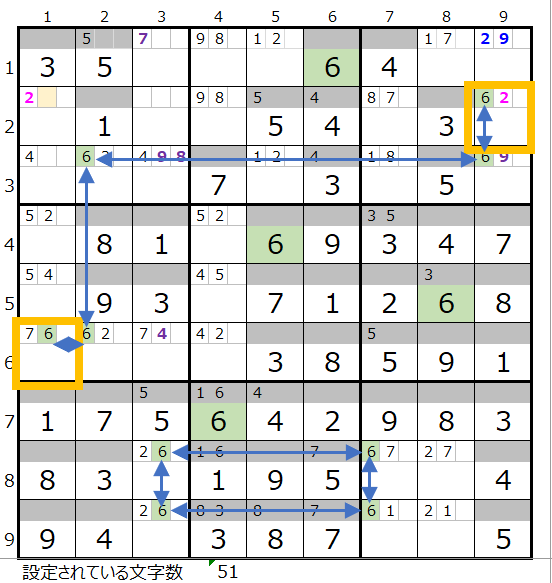
次に数字の「6」を見て行きます。

その前に飛んでいる数字「1」「3」「4」「5」は「解法その1～3」で既に数字が埋まっているために省略いたしました。

数字の「6」は背景色薄ベージュ色の2行1列のマス目のメモ欄に「6」が入れば良い事が解ります。

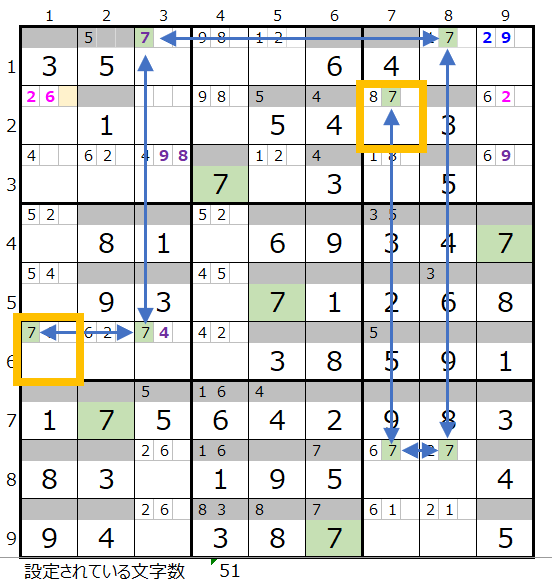
以下ご説明としては繰り返しになりますが、数字の「7」の場合は、背景色薄ベージュ色の2行1列のマス目のメモ欄に「7」が入れば良い事が解ります。

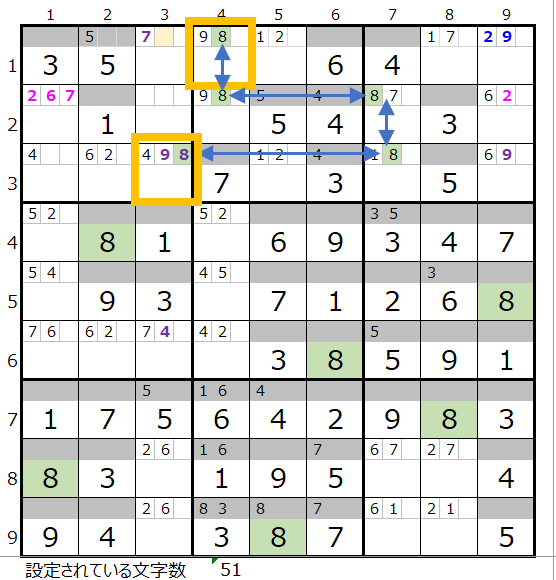
数字の「8」は背景色薄ベージュ色の1行3列のマス目のメモ欄に「8」が入れば良い事が解ります。

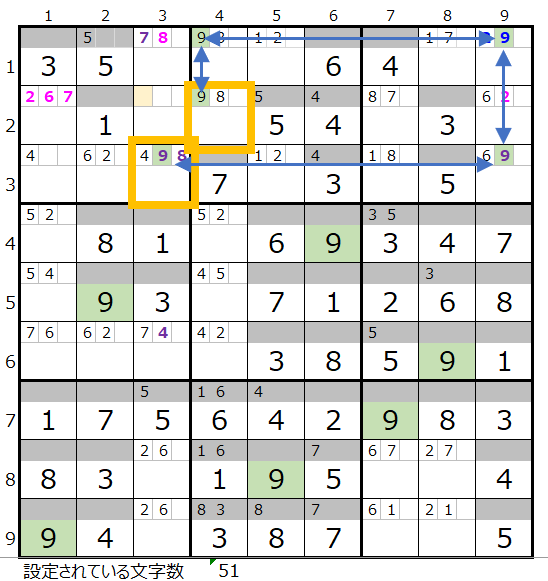
最後に、数字の「9」は背景色薄ベージュ色の2行3列のマス目のメモ欄に「9」が入れば良い事が解ります。

これですべての「行」と「列」で2つずつ数字をメモ欄に埋めることができました。

「行」と「列」で2つずつ数字があるという事は、ブロックで見た時にも同じように2つずつ数字が存在するはずです。
そうならない時は、経験上はどこかに誤りがあるだと思いますが、数学的に証明することはできていないので悪しからずご了承ください。

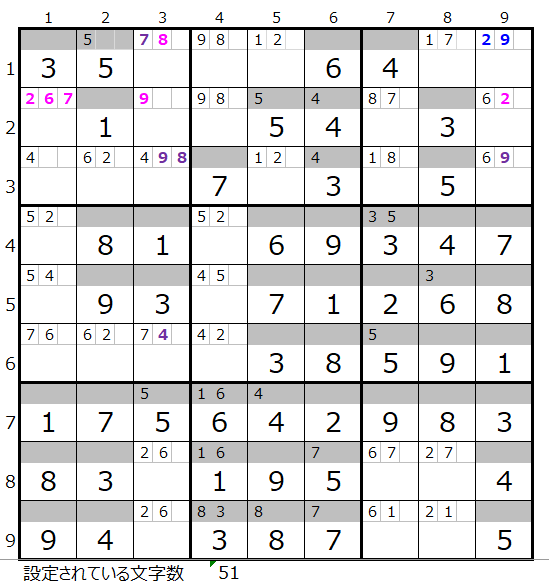
最終的な盤面は左図のようになります。

この状態を見ると、2行3列はメモ欄に数字の「9」しか入っていないので、「9」で確定のように思われるかもしれませんが、行方向、列方向ともに他の場所に「9」があるので、残念ながらそのように決める事はできません。

では「ここで何をするか?」と言いますと、下図をご覧ください。

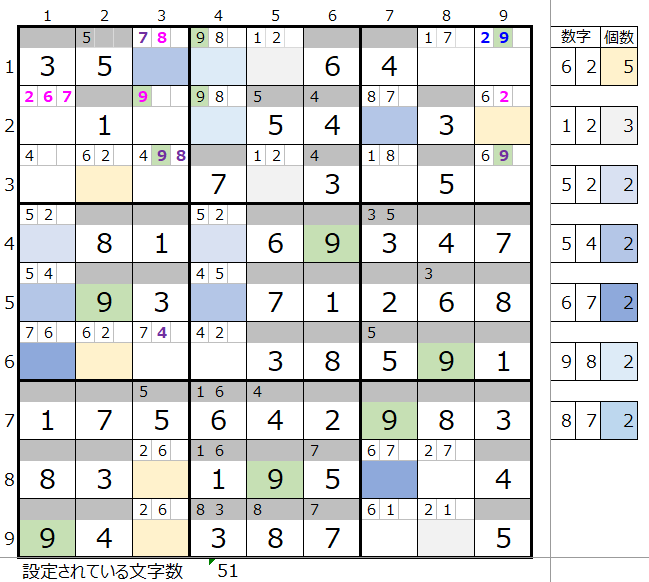
まず数字が設定されていない、すべてのマス目のメモ欄を調べて、数字の組み合わせの出現回数を求めます。

今回は「6」と「2」の組み合わせ個数が5つで最大になります。

そこで二択分岐は背景色薄ベージュ色のマス目のどこかを選び、そこに実際に数字を置いて解き進めることにします。

ただ、今回は「解法その4」で求まったマス目の数が少なく、となりますと「解法その4をやらなくても結果は見ていてたのでは?」というご指摘はごもっともでございます。

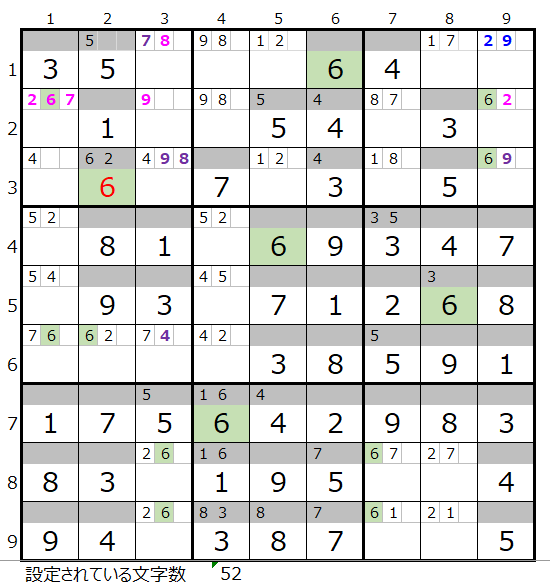
先ほどの問題の続きですが、3行2列のマス目を選び、「6」と「2」内の「6」を選択して解き進めて見たいと思います。

なお「同じ数字の組み合わせの中で、どの場所を選ぶのが良いか?」につきましても、考え方について次回ご説明いたいと存じます。

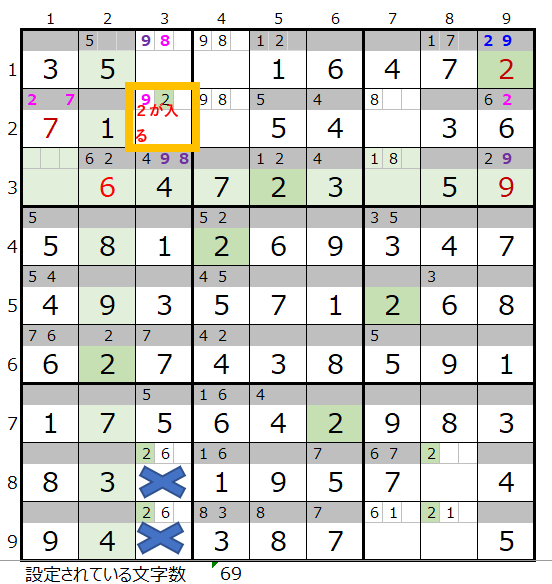
しばらく解き進めますと、3行9列に数字の「9」が入りますが、同じブロックに同じ数字の組み合わせを持つマス目が1行9列にあり、そこに数字の「2」が入ります。

そこでつぎに数字の「2」を調べると、左図黄枠に「2」が入るのですが、その場合残念ながら、左下のブロックで数字の「2」が入るマス目が無くなってしまい、解くことができないことが解ります。

ということで、3行2列に数字の「2」が入るパターンがどうなるか?につきましては、皆さまでご確認していただければ幸いです。