「書式を使用して難しい数独をどのように解くのか? 第1回概説」に記載した3つの解法とプラスαについて、複数回に分けて具体的に説明をしています。
今回は第3回目で「解法その2」になります。
今回の説明で使用する数独問題について
今回の説明で使用させていただく数独の問題は、下記サイトの2015年11月の問題集「数独問題集(達人級)」の2015/11/10の下段に掲載されているものを途中から使用させていただいております。
上記サイトには良質な問題が数多く掲載されていて、かつ無料ですが、コピーライトは問題を作られている数独無料問題集様がお持ちのものになりますので初期の盤面につきましては、上記サイトにてご確認いただけますようお願い申し上げます。
「解法その2」の具体的な動きの説明
「解法その1」は行、列の2方向とブロックで探したのですが、「解法その2」では行とブロック、または列とブロックで探す方法になります。
従いまして、これもごく一般的な解法になります。
行(横方向)または列(縦方向)で、1方向でターゲットを探し、ターゲットを含まないブロックで狙い目を見つけます。

今回も言葉だけでイメージするのは難しい事と存じますので、具体的な例でお話をいたします。
左の盤面は先ほどご紹介した「数独問題集(達人級)」の2015/11/10の下段に掲載されている問題を「設定されている数字」が28になるまで解き進んだものです。
メモ欄は「解法その1」だけを使って入れたものになります。
まずは数字の1から順番に行(横方向)、それから列(縦方向)で1行目から9行目、1列目から9列目まで順番に確認して行きます。
その上でやるべきことは下記の2点です。
- ひとつの行または列で狙い目が1つしかなければ、その狙い目にターゲットをセットします。
- ひとつの行または列で狙い目が2つの場合はメモ欄にターゲットをセットします。
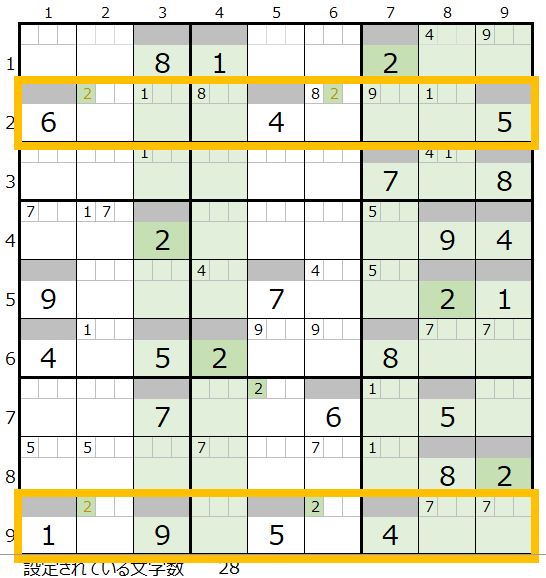
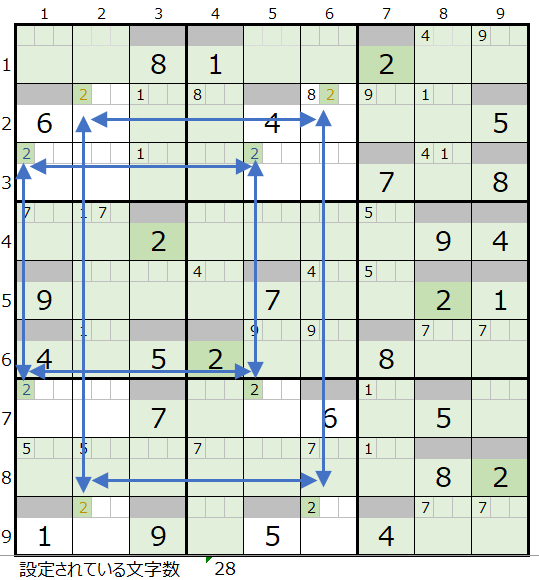
左図は数字の2が各行(横方向)で入る場所を確認して見た結果です。
なお背景色が付いてるのは、その列に数字の2が設定されていることを表しています。
注目していただきたのは、2行目と9行目の黄枠になります。
数字の2が入るマス目は、共に2列目と6列目の2か所(9行目は解法その1で6列のメモ欄には「2」が入っている状態ですが…)になるので、メモ欄に「2」を入力します。
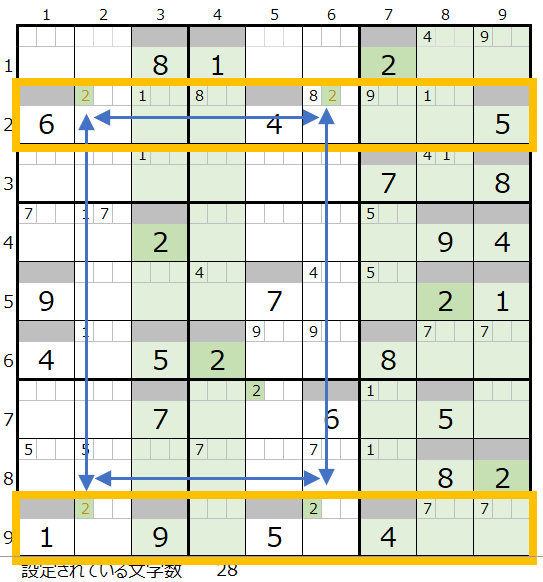
今回のように長方形になるのはレアケースにはなりますが、 このような場合は、対角線となる場所に「2」が入ることになり、パターンとしては「2行2列と9行6列」、「9行2列と2行6列」の2通りに絞られます。
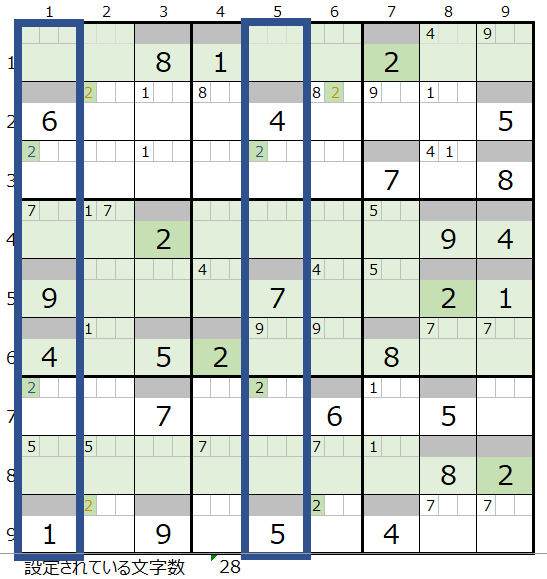
今回の問題には更なるレアケースの設定があります。
ここで今度は各列(縦方向)(先ほどは行方向でしたが…)で数字の2が入る場所を確認します。
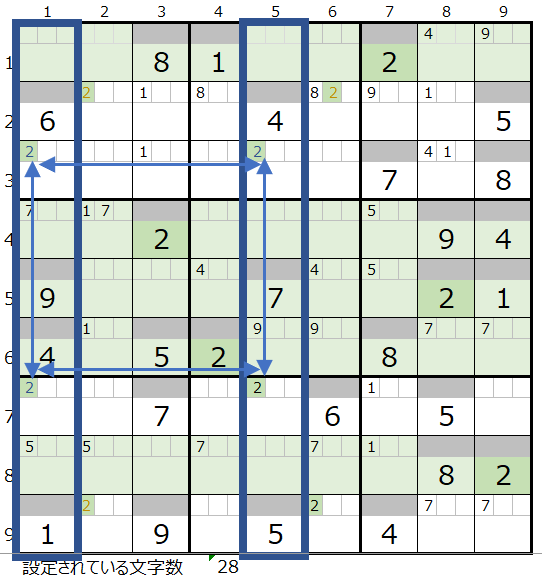
そうすると左図のように、1列と5列の青枠の3行目と7行目の2か所に新たに長方形の形で入ることが分かります。
そういう意味では、今回のケースはかなり特殊なものになりますが、同一ブロックのなかに同じ数字で2つの長方形が存在するとなると、数字の「2」が入るパターンとしては、下図の2つの背景色でどちらか一方になります。
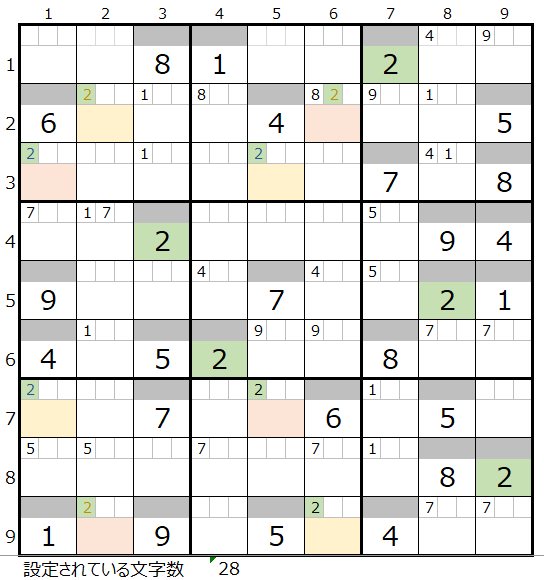
どちらかの背景色の内の一つで数字の「2」が決まると、残りの3か所でも数字の「2」が決まることになります。
突然ですがここで問題です
実は上記の盤面にはもう一つの長方形が隠されています。
その数字が何になるか?を考えてみてください。
なお、解答は本文の最後に掲載いたします。
今回の問題で「解法その2」による効果は?
今回の問題は2つ長方形があるというかなり特殊な形になりましたが、ただしそれによって得られた効果となりますと、数字の「2」のメモ欄が「2」を含まないすべてのブロックで埋まったという以外には残念ながらありません。
やりはインパクトとしては、「解法その1」の2方向から攻める手法に比べると弱くなってしまいます。
実際に、この問題でも「2」のメモ欄がすべて埋まっただけでその後は、まだご説明していない「解法その3」を使っても手詰まりとなってしまいます。
こちらもまだご説明していない「解法その4」につきましては、何と設定されている文字数が40文字前後無いと使用することが困難な解法になっておりまして、今回の場合は出番がありません。
そうなりますと、この問題を解くためにはここで最終手段である「二択分岐」をする必要があります。
「解法その3」を使うと二択分岐の候補となるマス目はいくつか存在する事が解りますが、折角数字の「2」に関して「解法その2」で特異点を発見できているので、それを二択分岐で使うのが良い認識です。
ということで、先ほどの2つの背景色の内、薄赤の方を使って解き進めて見たいと思いますが、事細かに説明してしまうと、本問の良さを損ねることになりますので、要所だけをお示ししたく存じます。
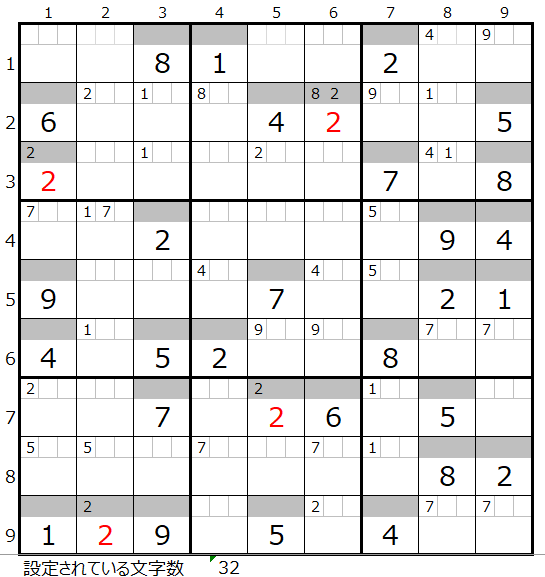
2つのパターンの内の一つである、「3行1列」に数字の「2」が入る場合について仮置きして見ます。
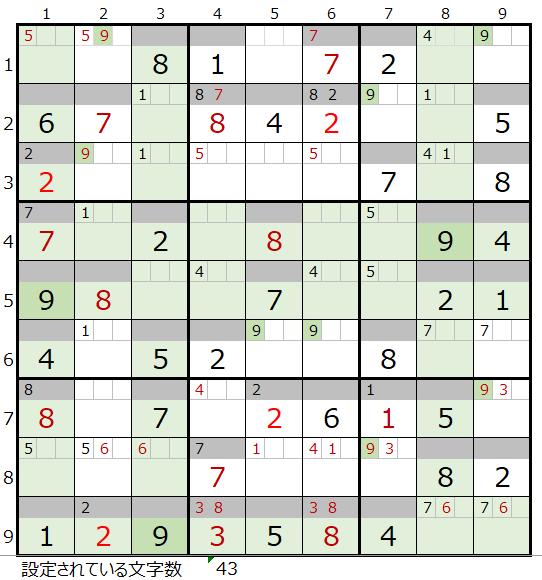
途中で、左図のような盤面となり、行き詰った感じになりますが、これは前回『「解法その1」のバリエーション』としてご説明した解法で、その先に進むことができます。
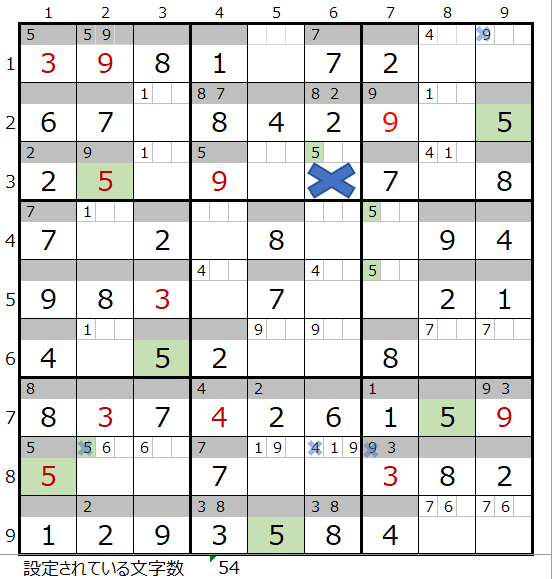
実は、このパターンでは最後までたどり着くことができません。
どの時点で解けないと判断するのか?につきましては、いろいろなバリエーションがあることと存じます.
2つのパターンの内のひとつは解けないことがわかりました。
もうひとつのパターンについては是非皆様で試してみていただければ幸いです。
まとめ
解法その2の基本的にパターンについて、ご説明をしましたが、如何でしたでしょうか?
長方形になるのはレアケースではありますが、探すとひとつの行または列で狙い目が2つケースは良くあることと存じます。
ただその効果となりますと、先の見出しでも書きましたが「解法その1」のようなインパクトを得ることはできません。
そうは言うものの、人の力で解答を導き出すためには、僅かな情報であっても無駄にすることが大切であると思います。
次回は解法その3についてご説明いたします。
以上最後までご一読いただきありがとうございました。
p.s.
途中でお出しした問題の解答は数字の「8」になります。
2019/8/28追記
現在「二択分岐はなるべく使わない形で解けないか?」「その場合にはどのような書式が良いか?」という形で見直しを進めています。
二択分岐を使用しない意図としましては、やはり解けないバターンの場合の手戻り感と、行き詰った時の「やるせなさ」を回避したいという思いからです。
整い次第、記事でご紹介する予定です。
ご迷惑をお掛けしますが、何卒よろしくお願い申し上げます。

