PR

Excel VBAで緯度・経度を平面直角座標に変換する

H31年行政区域オートシェイプ図形
2020.09.10
この記事は約21分で読めます。

「地図のオートシェープ図形」とグラフ散布図の使用事例としてご提供しているマクロ有効ブック「グラフ散布図使用事例」において使用している「緯度経度を平面直角座標に変換するためのExcel VBA」をご説明いたします。

なおExcel 2016のバージョンは2007、ビルド13029.20308で確認をしています。

スポンサーリンク

国土地理院の「測量計算サイト」に掲載されている計算式のプログラム化

表題の「測量計算サイト」の「平面直角座標への換算」に計算式のリンクが掲載されています。

平面直角座標への換算　計算式
vldb.gsi.go.jp

しかし筆者にとってはとても難解で詳細を理解するには至らないのですが、大変ありがたい事にこの難解な計算式を読み解かれて、計算単位をラジアンに統一し、さらに変数の依存関係を可視化した上でPython言語を使って実装したプログラムを公開されているサイトがございます。

緯度経度と平面直角座標の相互変換をPythonで実装する - Qiita
1. はじめにここでは緯度経度 <-> 平面直角座標の実装（Python）のみ記す。変換式の詳細や平面直角座標系の解説は、長くなるので別途ブログに書いた。緯度経度と平面直角座標の相...
qiita.com

そこで「平面直角座標への換算」の計算ロジックにつきましては、上記のサイトのPython言語のコーディングをExcel VBAにコンバージョンをして実装しています。

ただし計算の数値精度につきましてはVBAとPythonでは微妙な誤差がありますので、後段でご説明したく存じます。

なお計算誤差のご説明をする前に、Excel VBAならではの制約事項を2点ほどお話してさせていただきます。

①Excel で浮動小数点演算の結果が正しくない場合がある

少し開き直ったような表現ではありますが実はこの表題はMIcrosoftのドキュメントのトラブルシューティングのページに存在するトピックの題名になります。

浮動小数点演算が Excel で不正確な結果をもたらす可能性がある - Microsoft 365 Apps
浮動小数点演算が Excel で不正確な結果をもたらす可能性があることについて説明します。
learn.microsoft.com

このページは機械翻訳のため読み難いのですが、「正しくならない理由」を非常に簡単に意訳してまとめると下記のようになる認識です。

理由

・IEEE 754 の仕様に基づき浮動小数点数を格納および計算する場合、丸めまたはデータの切り捨てが原因で、一部の数値または数式の結果に影響することがあります。(ExcelはIEEE 754 の仕様に基づいて設計されています)

・例えば分数1/10 は10進数の値で「0.1」 として表現できますが、コンピュータ処理のためのバイナリ形式では次のような「繰り返し2進値」となります。従ってどこかで丸めまたはデータの切り捨てをする必要があります。

「0001100110011100110011 (以降繰り返し)」

・すべてのコンピューターに、処理できる最大数と最小数があり、Excelの(倍精度)浮動小数点数の格納方法では最大数は1.79769313486232 E + 308 で、最小の正の数は 2.2250738585072 E-308になります。

・(倍精度)浮動小数点数は、65ビット範囲内の3つの部分 (符号、指数、および仮数) 内に情報が2進で格納され、実際の数が格納される52ビット仮数に納まるのは十進数で15桁ぶんに当たる精度となり、この制限は、厳密に IEEE 754 仕様に従うことによる結果です。

この中で例示されているセルに次の式を入力する例は、事象を実際に目で確認する事ができます。

=(43.1-43.2) + 1

上記式を入力したセルをマウス右ボタンでクリックし、ショートカットメニューから「セルの書式設定」を選択し、「表示形式」タブの分類で「数値」を選び、小数点以下の桁数を「15」に設定すると式の答えであるはずの「0.900000000000000」ではなく「0.899999999999999」と表示されてしまいます。

※ちなみに有効桁数15桁というのは、整数がゼロの場合は、小数点以下でゼロではない桁から以下15桁が有効桁数になります。

上記の式は値が「43.1」だから発生するのではなく、ひとつづつ引いて確認すると「32.1」まで1単位で同様の結果になります。

なお「=(31.1-31.2) + 1」にすると今までと異なる「0.900000000000002」という小数点以下15桁目が「2」という値になります。この現象は「16.1」では1単位で同様に起こります。

ちなみに「15.1」から「0.1」までは1単位で正しい値で表示されます。

②Excelの数学関数は倍精度浮動小数点で値を返します

今回の数式で使用する下記の関数はすべて「倍精度浮動小数点数(=Double)」で結果を返します。

Exp関数、Log関数、Sqr関数、Sin関数、Cos関数、Tan関数、Atn関数

そのため、倍精度浮動小数点よりも精度の高い十進数データ(Decimal)型を使用することはできません。

従いまして採り得る最大限の精度としては倍精度浮動小数点の15桁になります。

Excel VBAでのコンバージョン

実際のコーディング内容をご紹介いたします。

なお最初にコーディングにおける考慮事項を列挙いたします。

  1. 計算式に関わる変数はすべて倍精度浮動小数点にしています。
  2. 計算式で使用されるリテラル定数には倍精度浮動小数点の型文字「#」を付けています。
    • なお確認した範囲で「#」を付けることで計算精度が向上することはありませんが、「#」を付ける事でデータ型判断がショートカットされる事を期待しています。ただし実際に処理時間を計測した分けではありませんのでお含み置きいただければ幸いです。
  3. 座標系原点の緯度・経度で小数点以下が続く時は有効桁数17桁にして、系番号をパラメータで受けて変換する形でコーディングしています。
    • 17桁にしないと演算誤差に影響が出る事を確認しています。
      ただそうなると、少し腑に落ちないのですが、文字列から倍精度浮動小数点型変数に変換した時には桁落ちせず、その後のラジアン変換の計算で影響が出ているものと思われます。
  4. Excelに組み込まれていない数学関数は導出式を関数化して対応しています。
  5. 角度とラジアンの変換は下記の関係性から計算しています。
    • π[ラジアン] = 180° = Atn(1)*4
  6. Pythonで実装されている特殊な行列演算式などはそれぞれ関数化して対応しています。
    • np_dot・np_sum・np_multiply・np_cos・np_sin・np_cosh・np_sinh・np_arange
  7. NaNは今回発生しないと思われる「999999999」を使って実装しています。
Attribute VB_Name = "Module1"
Option Explicit
Dim NaN As Double
'系番号から座標系x原点とy原点を取得するための配列
Const TargetX As String = "0,33,33,36,33,36,36,36,36,36,40,44,44,44,26,26,26,26,20,26"
Const TargetY As String = "0,129.5,131,132.16666666666667,133.5,134.33333333333333,136,137.16666666666667,138.5,139.83333333333333,140.83333333333333,140.25,142.25,144.25,142,127.5,124,131,136,154"
'定数 (a, F: 世界測地系-測地基準系1980（GRS80）楕円体)
Dim m0 As Double
Dim a As Double
Dim F As Double
'セル関数として呼ばれる--平面直角座標の緯度を返す
Public Function calc_x(phi_deg As Double, lambda_deg As Double, groupNum As Integer) As Double
Attribute calc_x.VB_Description = "十進法緯度・経度を指定された平面直角座標の緯度（Ｘ座標）に変換します。"
Attribute calc_x.VB_ProcData.VB_Invoke_Func = " \n14"
    calc_x = Split(calc_xy(phi_deg, lambda_deg, CDbl(Split(TargetX, ",")(groupNum)), CDbl(Split(TargetY, ",")(groupNum))), ",")(0)
End Function
''セル関数として呼ばれる--平面直角座標の経度を返す
Public Function calc_y(phi_deg As Double, lambda_deg As Double, groupNum As Integer) As Double
Attribute calc_y.VB_Description = "十進法緯度・経度を指定された平面直角座標の経度（Y座標）に変換します。"
Attribute calc_y.VB_ProcData.VB_Invoke_Func = " \n14"
    calc_y = Split(calc_xy(phi_deg, lambda_deg, CDbl(Split(TargetX, ",")(groupNum)), CDbl(Split(TargetY, ",")(groupNum))), ",")(1)
End Function
'
Private Function calc_xy(phi_deg As Double, lambda_deg As Double, phi0_deg As Double, lambda0_deg As Double) As String
'緯度経度を平面直角座標に変換する
'input:
' (phi_deg, lambda_deg): 変換したい緯度・経度[ 十進法度]（分・秒でなく小数）
' (phi0_deg, lambda0_deg): 平面直角座標系原点の緯度・経度[ 十進法度]（分・秒でなく小数）
'output:
' x: 変換後の平面直角座標[m]
' y: 変換後の平面直角座標[m]

'緯度経度・平面直角座標系原点をラジアンに直す
'
NaN = CDbl(999999999)
m0 = CDbl(0.9999)
a = CDbl(6378137)
F = CDbl(298.257222101)
'
Dim phi_rad As Double, lambda_rad As Double, phi0_rad As Double, lambda0_rad As Double
'
    phi_rad = fnradians(phi_deg)
    lambda_rad = fnradians(lambda_deg)
    phi0_rad = fnradians(phi0_deg)
    lambda0_rad = fnradians(lambda0_deg)
'
'① n, A_i, alpha_iの計算
Dim n As Double
Dim A_array() As Double, alpha_array() As Double
    n = 1# / (2# * F - 1#)
    A_array = fnA_array(n)
    alpha_array = fnalpha_array(n)
'
'②S_, A_の計算
Dim A_ As Double, S_ As Double
    A_ = ((m0 * a) / (1# + n)) * A_array(0)  'ｍ
    S_ = ((m0 * a) / (1# + n)) * (A_array(0) * phi0_rad + np_dot(A_array, np_sin(2# * phi0_rad, np_arange(1, 5)))) 'ｍ
'
'③ lambda_c, lambda_sの計算
Dim lambda_c As Double, lambda_s As Double
    lambda_c = Cos(lambda_rad - lambda0_rad)
    lambda_s = Sin(lambda_rad - lambda0_rad)
'
'④t, t_の計算
Dim t As Double, t_ As Double
    t = fnsinh(fnarctanh(Sin(phi_rad)) - ((2# * Sqr(n)) / (1# + n)) * fnarctanh(((2# * Sqr(n)) / (1# + n)) * Sin(phi_rad)))
    t_ = Sqr(1# + t * t)
'
' ⑤ xi', eta'の計算
Dim xi2 As Double, eta2 As Double
    xi2 = Atn(t / lambda_c)    ' [rad]
    eta2 = fnarctanh(lambda_s / t_)
'
'⑥ x, yの計算
Dim x As Double, y As Double
    x = A_ * (xi2 + np_sum(np_multiply(alpha_array(), np_multiply(np_sin(2# * xi2, np_arange(1, 5)), np_cosh(2# * eta2, np_arange(1, 5)))))) - S_ ' ｍ
    y = A_ * (eta2 + np_sum(np_multiply(alpha_array(), np_multiply(np_cos(2# * xi2, np_arange(1, 5)), np_sinh(2# * eta2, np_arange(1, 5))))))     ' ｍ
'
    calc_xy = x & "," & y
    
End Function
'
Function fnA_array(dn As Double) As Double()
Dim Ar(5) As Double
    Ar(0) = 1# + (dn ^ 2) / 4# + (dn ^ 4) / 64#
    Ar(1) = -(3# / 2#) * (dn - (dn ^ 3) / 8# - (dn ^ 5) / 64#)
    Ar(2) = (15# / 16#) * (dn ^ 2 - (dn ^ 4) / 4#)
    Ar(3) = -(35# / 48#) * (dn ^ 3 - (5# / 16#) * (dn ^ 5))
    Ar(4) = (315# / 512#) * (dn ^ 4)
    Ar(5) = -(693# / 1280#) * (dn ^ 5)
'
    fnA_array = Ar()
End Function
'
Function fnalpha_array(dn As Double) As Double()
Dim Ar(5) As Double
    Ar(0) = NaN  'NaN
    Ar(1) = (1# / 2#) * dn - (2# / 3#) * (dn ^ 2) + (5# / 16#) * (dn ^ 3) + (41# / 180#) * (dn ^ 4) - (127# / 288#) * (dn ^ 5)
    Ar(2) = (13# / 48#) * (dn ^ 2) - (3# / 5#) * (dn ^ 3) + (557# / 1440#) * (dn ^ 4) + (281# / 630#) * (dn ^ 5)
    Ar(3) = (61# / 240#) * (dn ^ 3) - (103# / 140#) * (dn ^ 4) + (15061# / 26880#) * (dn ^ 5)
    Ar(4) = (49561# / 161280#) * (dn ^ 4) - (179# / 168#) * (dn ^ 5)
    Ar(5) = (34729# / 80640#) * (dn ^ 5)
'
    fnalpha_array = Ar()
End Function
'
Function np_dot(da1() As Double, da2() As Double, Optional sta As Integer = 1) As Double
Dim rt As Double
Dim i As Integer
    rt = 0#
    For i = sta To UBound(da1)
        If da1(i) <> NaN And da2(i) <> NaN Then rt = rt + da1(i) * da2(i)
    Next i
'
    np_dot = rt
End Function
'
Function np_sum(da1() As Double, Optional sta As Integer = 1) As Double
Dim rt As Double
Dim i As Integer
    rt = 0#
    For i = sta To UBound(da1)
        If da1(i) <> NaN Then rt = rt + da1(i)
    Next i
'
    np_sum = rt
End Function
'
Function np_multiply(da1() As Double, da2() As Double, Optional sta As Integer = 1) As Double()
Dim i As Integer
Dim rt() As Double
ReDim rt(UBound(da1))
    For i = sta To UBound(da1)
       If da1(i) <> NaN And da2(i) <> NaN Then rt(i) = da1(i) * da2(i)
    Next i
'
    np_multiply = rt()
End Function
'
Function np_cos(dn As Double, da1() As Double, Optional sta As Integer = 1) As Double()
Dim i As Integer
Dim rt() As Double
ReDim rt(UBound(da1))
    For i = sta To UBound(da1)
        If da1(i) <> NaN Then rt(i) = Cos(dn * da1(i))
    Next i
'
    np_cos = rt()
End Function
'
Function np_sin(dn As Double, da1() As Double, Optional sta As Integer = 1) As Double()
Dim i As Integer
Dim rt() As Double
ReDim rt(UBound(da1))
    For i = sta To UBound(da1)
        If da1(i) <> NaN Then rt(i) = Sin(dn * da1(i))
    Next i
'
    np_sin = rt()
End Function
'
Function np_cosh(dn As Double, da1() As Double, Optional sta As Integer = 1) As Double()
Dim i As Integer
Dim rt() As Double
ReDim rt(UBound(da1))
    For i = sta To UBound(da1)
        If da1(i) <> NaN Then rt(i) = fncosh(dn * da1(i))
    Next i
'
    np_cosh = rt()
End Function
'
Function np_sinh(dn As Double, da1() As Double, Optional sta As Integer = 1) As Double()
Dim i As Integer
Dim rt() As Double
ReDim rt(UBound(da1))
    For i = sta To UBound(da1)
        If da1(i) <> NaN Then rt(i) = fnsinh(dn * da1(i))
    Next i
'
    np_sinh = rt()
End Function
'
Function np_arange(sta As Integer, sto As Integer, Optional ste As Integer = 1) As Double()
Dim i As Integer
Dim rt() As Double
ReDim rt(sto)
    For i = sta To sto Step ste
        rt(i) = CDbl(i)
    Next i
'
    np_arange = rt()
End Function
'
Function fnradians(dn As Double) As Double
    fnradians = dn / 45# * Atn(1#)
End Function
'
Function fncosh(dn As Double) As Double
    fncosh = (Exp(dn) + Exp(-dn)) / 2#
End Function
'
Function fnsinh(dn As Double) As Double
    fnsinh = (Exp(dn) - Exp(-dn)) / 2#
End Function
'
Function fnarctanh(dn As Double) As Double
    fnarctanh = Log((1# + dn) / (1# - dn)) / 2#
End Function

上記で作成したVBA関数の使い方

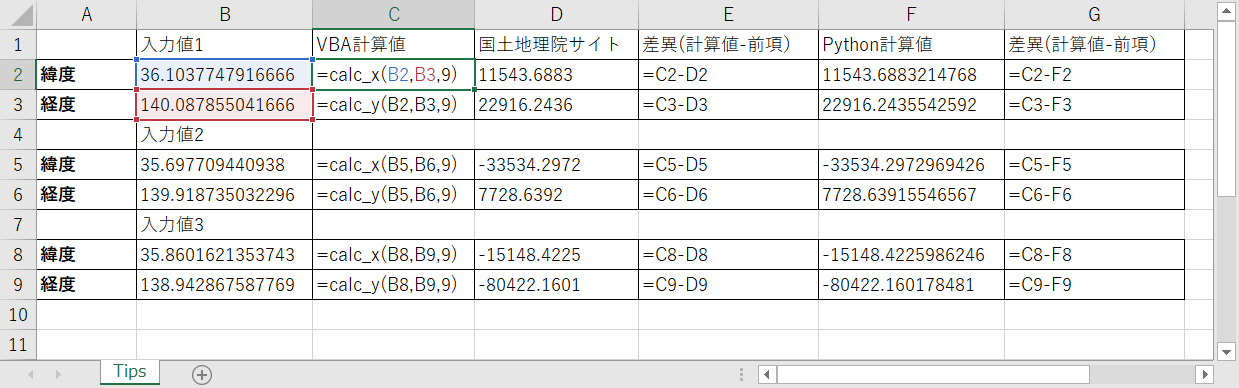
左図の表は、B列に緯度・経度が入力されていて、その値をC列の関数が参照しています。

セルでの関数の呼び方は、緯度、経度の順に下記になります。

=calc_x(緯度,経度,系番号)
=calc_y(緯度,経度,系番号)

引数は両者同じで、関数名の最後が、緯度は「x」、経度は「y」が違うところです。

緯度、経度の指定の仕方は、上図のようにセル指定でも、値を直接指定する形でもどちらでも大丈夫です。

なお指定する緯度・経度の桁数は、日本であれば、経度は「整数2桁に小数点以下最大13桁」、経度は「整数3桁に小数点以下最大12桁」になります。

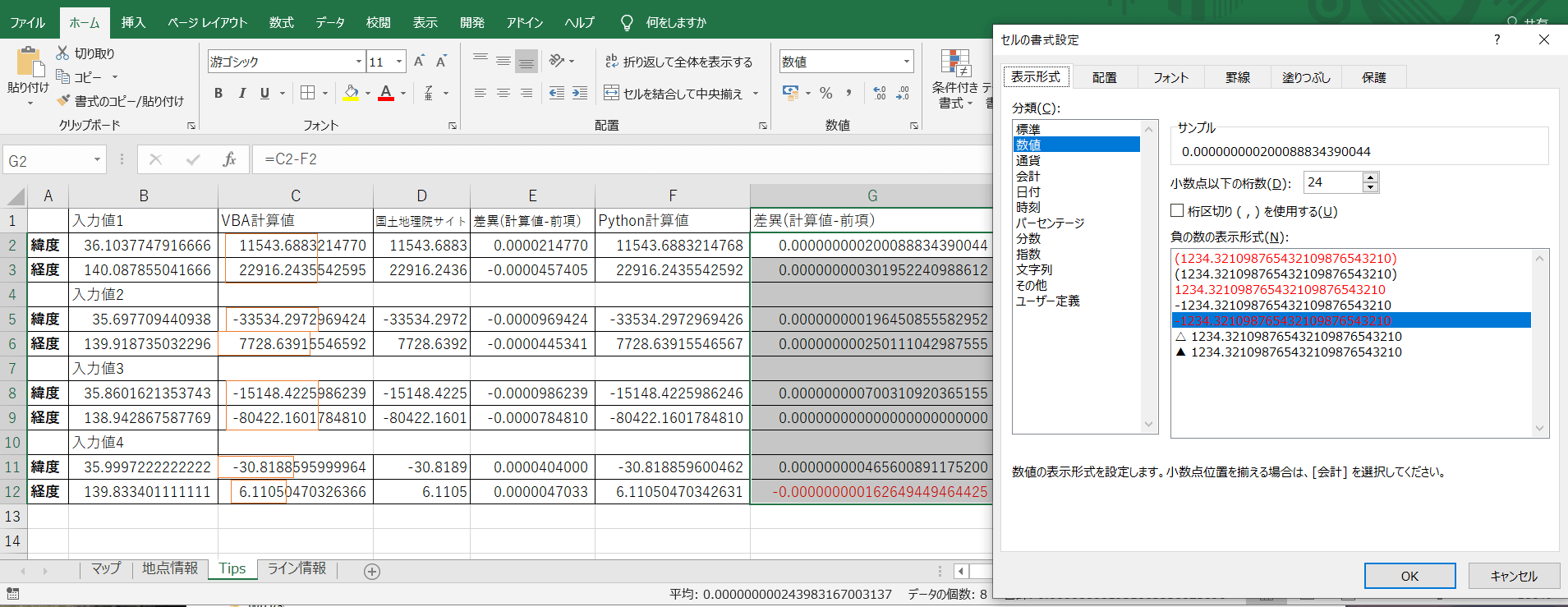
計算結果は左図になります。

なお左図にはD列に「国土地理院測量計算サイト」での結果と、F列に「Pythonで計算をした値」を掲載しています。国土地理院サイトの結果は小数点以下4桁で固定されているようです。

併せてE列とG列にVBAの計算結果との差異を表示しています。

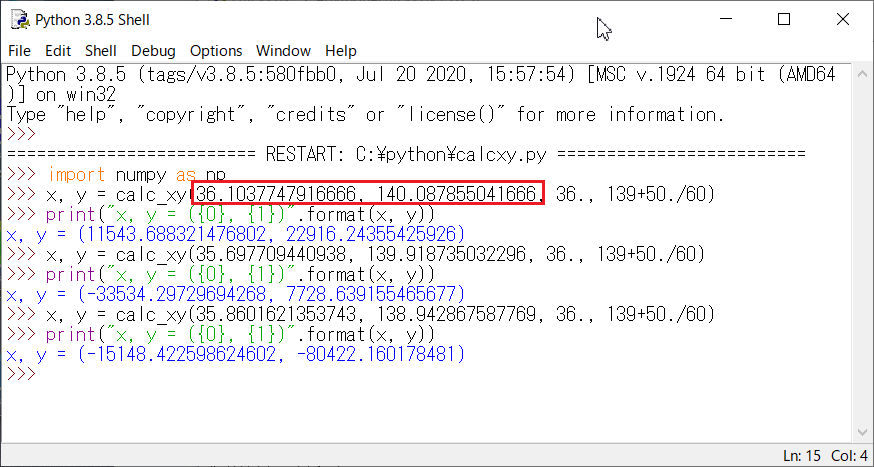
Python 3.8.5での実行結果は左図になります。

なお精度比較をする上で、Pythonでの緯度、経度の指定の桁数はVBAと併せて最大15桁としています。

Pythonでは実行結果は最大17桁で返ってきているので、本当は同程度が有効桁数になると推察されます。

ただ、そうした場合にはVBAの実行結果との差異が大きくなってしまうため同一条件で比較していますのでお含み置きいただければ幸いです

精度比較

平面直角座標で変換される値の単位はメートルになります。

となりますと「日本の平面座標系」で採り得る値としては大きくても数百キロメートル、つまり整数部は0桁から6桁となり、都合小数点以下は9桁から15桁が考えられる範囲になります。

Python計算値との比較

前章でもご説明いたしまたが、Pythonの戻り値は最大17桁になるのですがその値をExcelのセルにセットすると15桁で切り捨てられてしまいます。

従いまして精度比較は15桁で行っています。

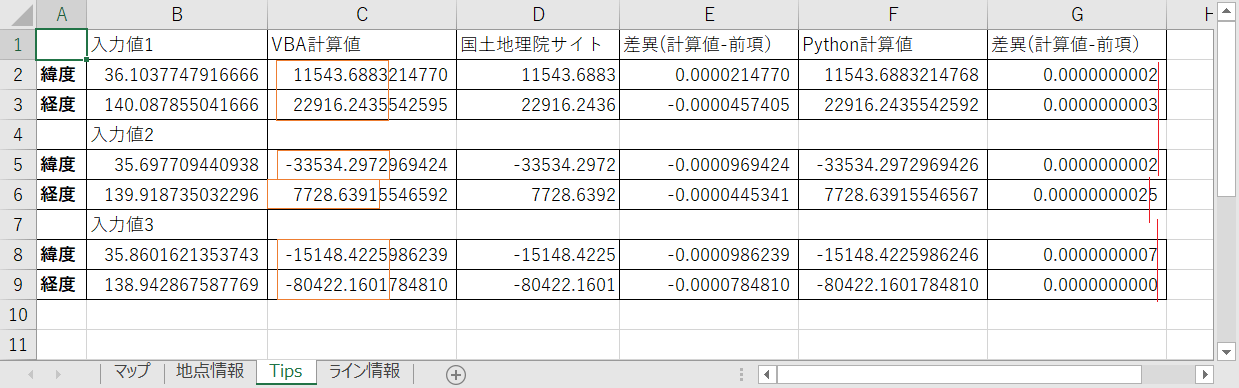
左図G列のようにVBA計算値とPython計算値の差異はすべて小数点以下10桁目に出現している事が解ります。

となると差異は有効桁数15桁の一番最後に現れるように思えますが、入力値2の経度は整数部が4桁、小数点以下11桁になるのですが、他と同様に10桁目に差異が現れています。

ただ一例だけでは少々気になるので左図では先ほどの結果に入力値4を追加しました。この入力値4は緯度が整数部2桁、経度は整数部1桁になるような地点を選んで設定してあります。

その結果としてはその他と同様に小数点以下10桁目に差異が現れています。

以上から、「差異は有効桁数の最終桁に出るわけでは無く小数点以下10桁目に出現する」と言えそうです。

では「なぜそうなるのか?」なのですが、考えられる理由としては、恐らく計算式の中で「②S_, A_の計算」での値が割と大きな数値になる事に関係がありそうです。

ちなみに入力値4では「S_=3985144.11602922」、「A_=6366812.40085647」でともに小数点以下8桁までが有効数字になっています。

「いやいや8桁と10桁では合わないでしょう」と思われまかもしれませんが、実は計算値は有効桁数よりも長く値が保持されていて、それをExelが15桁に「丸めまたは切り捨て」て表示させています。

先ほどご説明したG列の差異ですが、引き算によりいままで表示されていた有効桁数部分がゼロに置き換わるため、差異の始まる10桁目から最大24桁目までの15桁が設定を変更する事で表示されます。

ただ、「この表示される数字が有効数字なのか?」と言われると精度保証されない範囲にはなりますが、このようなデータがあることで正確には説明しきれませんが差異の出現が8桁から10桁に後ろ倒しになっているものと推察されます。

国土地理院サイトとの比較

前章でご説明した図のように差異としてはすべて「0.0001」を下回る結果になりますが、小数点以下4桁目は、「5桁目を四捨五入すると一致する」場合と「5桁目を切り捨てると一致する」場合の両者が混在しています。

となりますと完全に一致するのは小数点以下3桁目までで、「5桁目を四捨五入すると4桁目が「+1」ずれる場合がある」という状況である事が解ります。

ただし地図的には「0.1ミリメートル」という誤差は、誤差の許容範囲内であるという認識です。

最後に

VBAとPythonの計算結果の差異につきましては、VBAの数学関数がDecimal対応されれば解消できると思います。

と言いますのはPythonにもVBAと同様な「浮動小数点演算の問題」は存在しているのですが、結果を17桁の有効数字に丸めている点がVBAとの差になって表れている認識です。

15. Floating Point Arithmetic: Issues and Limitations
Floating-point numbers are represented in computer hardware as base 2 (binary) fractions. ...
docs.python.domainunion.de

ただどちらにしても地図を利用する際の誤差としてミリ単位であれば現状では気にならない範囲である事と存じます。

ちなみに日本版GPS衛星「みちびき」での位置精度は特別な機器を利用しない場合は数メートル、利用した場合は数センチになるようです。

「日本版GPS“みちびき”本格始動で数センチ級精度の位置情報取得が可能」は本当か
衛星測位に関し、複数のアプリ開発者の、真偽に疑問符が付く言説に接した。それは、「日本版GPSが本格始動すれば、数センチの精度で位置情報の取得が可能」というものだ。スマホの測位機能だ...
atmarkit.itmedia.co.jp

以上最後までご一読いただき誠にありがとうございました。

スポンサーリンク